- #1
LightningInAJar
- 233
- 30
- TL;DR Summary
- How do I calculate the diameter of regular polygons with 1 as side length?
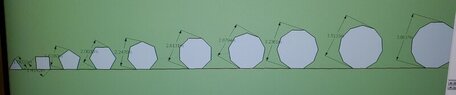
I measured the maximum diameters of 15 regular polygons with side lengths of one. Is there a way to calculate the maximum diameter for regular polygons of any number of sides without using pi or any nonterminating numbers?
03-Sided = 1
04-Sided = 1.4142
05-Sided = 1.6180
06-Sided = 2
07-Sided = 2.2470
08-Sided = 2.6131
09-Sided = 2.8794
10-Sided = 3.2361
11-Sided = 3.5133
12-Sided = 3.8637
13-Sided = 4.1484
14-Sided = 4.4940
15-Sided = 4.7834
03-Sided = 1
04-Sided = 1.4142
05-Sided = 1.6180
06-Sided = 2
07-Sided = 2.2470
08-Sided = 2.6131
09-Sided = 2.8794
10-Sided = 3.2361
11-Sided = 3.5133
12-Sided = 3.8637
13-Sided = 4.1484
14-Sided = 4.4940
15-Sided = 4.7834