Calculating the Time-Average Intensity of 3 Slits

[maxim07]

Homework Statement

If the three slits have equal widths, show that intensity I1 of light on the screen as a function of y is I = I/9[1 + 2cos(2pi * dy/Rw)]^2 where w is wavelength

If the width of the central slit is made twice as wide show that the intensity becomes I = 16I/9cos^4(pi*dy/Rw)

Relevant Equations

Sin/cosine addition formulas

Here’s an image of the equations better layed out

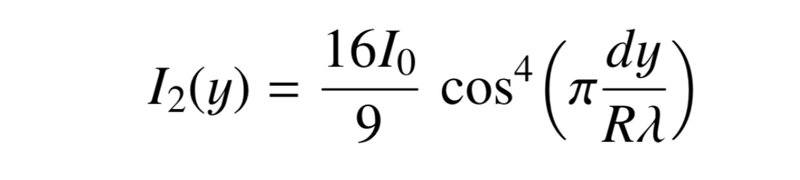
here’s the solution, I don’t understand how they are squaring it to get the time average

 

[Steve4Physics]

I don’t understand how they are squaring it to get the time average

Your problem description is incomplete, e.g. no diagram or definition of all symbols. (Though the missing information may not be necessary to answer your question.)

And you haven’t actually explained your difficulty.

Do you understand up to the part where the total (electric) field amplitude as a function of $y$ is given by $Asin(1+2cos\phi)$ where $\phi = \frac {2\pi dy}{R\lambda}$?

Remember, intensity is proportional to the square of the amplitude of the electric field. What is the maximum possible value of $(1+ 2cos\phi)^2$?

 

[maxim07]

I understand up to Asin(1+2cosφ). The max value of (1+2cosφ)^2 = 9 so you have to divide I₀ by 9. I understand that now, but if the (1+2cosΦ) is the amplitude then the sinx must get averaged, but I thought that would introduce a factor of 1/2?

 

[TSny]

The constant $I_0$ is defined to be the total intensity for $y = 0$ for the three equal-sized slits. So, the resultant expression for $I(y)$ for this case must reduce to $I_0$ for $y = 0$.

$I_0$ already includes the contribution due to time averaging as well as any constants of proportionality between intensity and square of the amplitude.

 

[Steve4Physics]

.. if the (1+2cosΦ) is the amplitude then the sinx must get averaged, but I thought that would introduce a factor of 1/2?

Can I add this to what @TSny has said:

Remember $\phi = \frac {2\pi dy}{R\lambda}$.

The field at position y, time t can be expressed in full as, say:
$E(y,t) = Asin(1+2cos(\frac {2\pi dy}{R\lambda}))sin(ωt + α)$
so
$E(y,t)^2 = A^2sin^2(1+2cos( \frac {2\pi dy}{R\lambda}))sin^2(ωt + φ)$

The average of $sin^2(\text {anything})$ over a complete number of cycles is ½. So the time- average of the field at y is:
$<E(y,t)^2>_{time} = ½A^2sin^2(1+2cos( \frac {2\pi dy}{R\lambda}))$

(We definitely don’t want to average over y as we are interested in the intensity for each value of y!)