Calculation the resistance of a spherical shape

[green-fresh]

hello there!
I was reading about ohm rule in a MIT physics course and they calculate the resistance of a nested spherical shells like this :

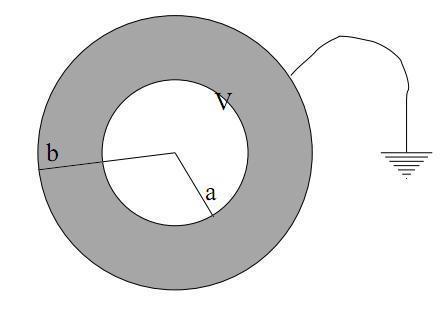
and they but the microscopic form of ohm's law which is :
J=\sigma_q E
and
I=A J
so
I=(4 \pi r^2 ) (\sigma_q E)
and
E=-\frac{\partial V}{\partial r}
and he said that the potential must be like this form
V=\frac{C}{r}+D
where : C and D are constant .
so my question is what is this form and why he did that and i could calculate the potential easily :
V_{ab}=\int E . dr.
thank you

 

[Petr Mugver]

For symmetry, the electric field is directed radially. Since there are no charges inside the conductor, the flux

\Phi=4\pi r^2 E

must be constant. The difference of potential between a and b is

\Delta V=\int_a^b\frac{\Phi dr}{4\pi r^2}=\frac{\Phi(b-a)}{4\pi ab}.

But, as you said, I=\sigma\Phi, so

\Delta V=\frac{I(b-a)}{4\pi ab\sigma}\equiv RI

and hence

R=\frac{(b-a)}{4\pi ab\sigma}

 

[green-fresh]

thank you i think it is solved now .