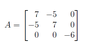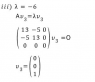sozener1
- 19
- 0
Im supposed to find the eigenvectors and eigenvalues of A
I found that eigenvalues are 2 12 and -6
then I found eigen vectors substituting -6 to lambda
and someone has told me I get 0 0 1 for eigenvector which I cannot understand why??
can anyone pleasezzzzzzzz explain why this is?
I found that eigenvalues are 2 12 and -6
then I found eigen vectors substituting -6 to lambda
and someone has told me I get 0 0 1 for eigenvector which I cannot understand why??
can anyone pleasezzzzzzzz explain why this is?