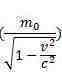Can Photon Energy Be Equated to Kinetic and Potential Energy?

[manifested]

If the energy of single photon of electromagnetic radiation is defined by its wavelength, could it also be set equal to its potential and kinetics?(I’m probably missing something)
Please check this statement:

Where :
h is planks constant
f is frequency.
m0 is rest mass
M is the relativistic mass
v is velocity


If rest mass of electron is zero then mc2 is zero therefore the total energy must be all kinetic(right?).
The only way I could see the kinetic energy not being zero is if somehow the relativistic mass is not zero…or maybe I got it completely wrong…?

Thx in advance.

 

[Dale]

The correct relativistic expression is:

$$E^2 = m_0^2 c^4 + p^2 c^2 = h^2 f^2$$
Where $m_0$ is the invariant mass, $p$ is the momentum, and the rest are as you have them above.

The expression is general and applies for both massless and massive particles, but a photon has an invariant mass of 0.

 

[manifested]

thx for response.

even so. if p is mass times the velocity, again it comes down the mass or at least the variant mass not being equal to zero.
maybe I'm not looking at it the right way but the variant mass of a particle being defined as

gives the value 0 devided by zero as $$v\rightarrow c$$ and as $$m_0$$ $$\rightarrow 0$$.

i guess the reason for my confusion is that if mass and energy are the same thing in different forms there must be a mass equivalent for a photon(right?)

 

[Dale]

even so. if p is mass times the velocity, again it comes down the mass or at least the variant mass not being equal to zero.
maybe I'm not looking at it the right way but the variant mass of a particle being defined as

gives the value 0 devided by zero as $$v\rightarrow c$$ and as $$m_0$$ $$\rightarrow 0$$.

Momentum is not mass times velocity in general. As you mention the formula you provided is not valid for photons. The general formula for momentum is de Broglie's formula:
$$p=\frac{h}{\lambda}$$
where $\lambda$ is the wavelength.

Which applies for both massive and massless particles.

i guess the reason for my confusion is that if mass and energy are the same thing in different forms there must be a mass equivalent for a photon(right?)

The term you are looking for is "relativistic mass". As you note, it is nothing more than another name for the total energy. Because we already have a perfectly good name for energy this term is generally deprecated. Usually the unqualified word "mass" refers to the "invariant mass" or "rest mass", $m_0$, but I tend to always explicitly say which definition of mass I am using just to avoid confusion.

 

[pmacias]

The energy of a photon is defined by its wavelength and is given by the equation E = hf, where h is Planck's constant and f is the frequency of the photon. This equation is derived from the wave-particle duality of electromagnetic radiation, where photons can be thought of as both waves and particles.

The potential and kinetic energy of a photon are not directly related to its energy, as photons do not have mass and therefore do not have a potential energy. The equation E = mc^2 only applies to particles with mass, such as electrons.

The only way for a photon to have kinetic energy is if it has a relativistic mass, which is a concept that is not applicable to photons. Therefore, the energy of a photon is solely determined by its wavelength and frequency, and cannot be equated to potential or kinetic energy.

I hope this helps to clarify the energy of a photon for you. If you have any further questions, please let me know.