I Can We Practically Measure the Gravitomagnetic Effect with Spinning Cylinders?

[olgerm]

I was thinking about an experiment to demonstrate gravitomagnetic effect. I did my calculations using gravitomagnetic model. It is not as accurate as general relativity, but GR should give similar predictions. I do not know if it would be possible to to this experiment in real life(are there enougth accurate sensors and tought materials).
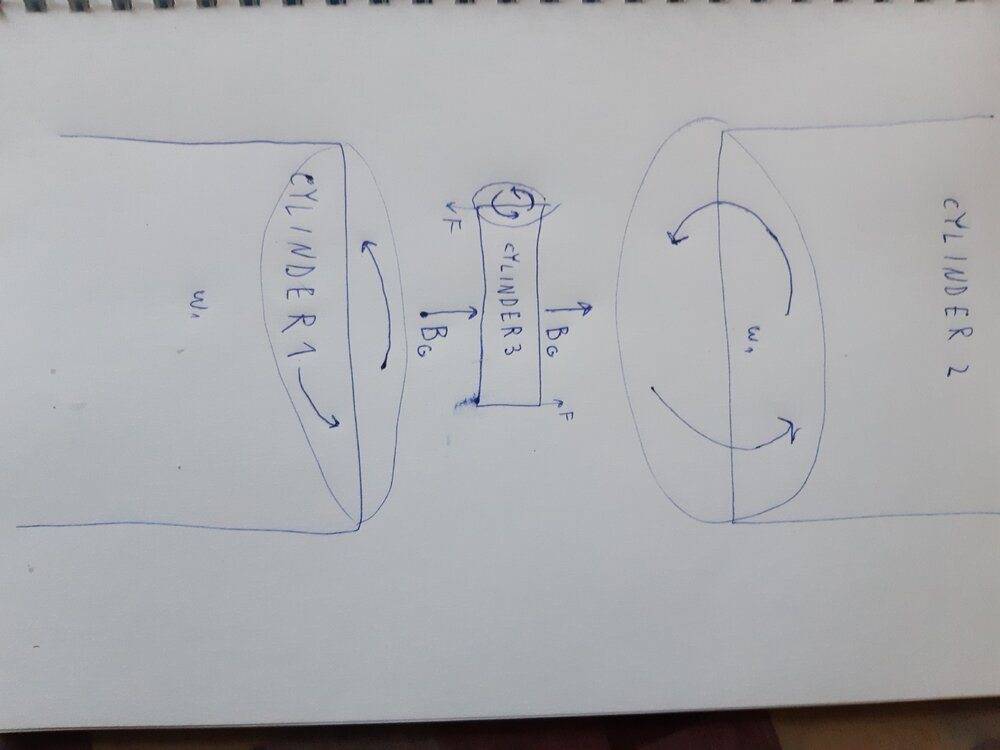
installations consists of three spinning cylinders. first to cylinders are for creating a magnetic field. last one is for detecting gravitomagnetic field. last cylinder under axis 90 degrees angle compared to first two cylinders.

gravitimagnetic field created by first two cylinders right between the cylinders: $B_G=\frac{\mu_G \omega_1 \rho_1 (r_2^2-r_1^2)}{2}$

• $\omega_1$ is angular speed of 1. and 2. cylinder.
• $\mu_G$is gravitomagnetic constant $\mu_G=\frac{2 2\pi G}{c^2} \approx 9.33\ 10^{-27} N/kg^2 s^2=9.33\ 10^{-27} s/kg$
• $\rho_1$ is density of 1. and 2. cylinder.
• $r_2$ is 1. and 2. cylinders outer radius.
• $r_1$ is 1. and 2. cylinders inner radius.

torque on third cylinder because of gravitomagnetic effect is crosswise to its angular speed and angular speed of first two cylinders.
$\tau=\frac{2\pi \rho_3 (R_2^4-R_1^4) \omega_3 B_G}{2}=\frac{\mu_G \omega_3 \rho_3 (r_2^2-r_1^2) 2\pi \rho_1 (R_2^4-R_1^4) \omega_1}{4}$

• $R_1$ is 3. cylinders inner radius.
• $R_2$ is 3. cylinders outer radius.
• $\rho_3$ is density of 3. cylinder.
• $\omega_3$ is angular speed of 3. cylinder.

What you think what is the highest value for $B_G$ and $\tau$ we could practically get?

Derivation of equations
gravitimagneticfield:
I used formula $B=\mu n I$ from http://hyperphysics.phy-astr.gsu.edu/hbase/magnetic/solenoid.html. Using similarities between gravitomagnetism and electromagnetism: $B_G=\mu_G n I_G=\frac{d^2m}{dl dt} \mu_G=\mu_G \frac{d^2m}{dl dt}=\mu_G \int_{r_1}^{r_2}(dr \rho v(r))=\mu_G \int_{r_1}^{r_2}(dr \rho \omega r)=\mu_G \rho \omega \int_{r_1}^{r_2}(dr r)=\frac{\mu_G \rho \omega (r_2^2-r_1^2)}{2}$

magnetic moment:
I used formula $m ={\frac {1}{2}}\iiint _{V}\mathbf {r} \times \mathbf {j} \,{\rm {d}}V$ from https://en.wikipedia.org/wiki/Magnetic_moment .
using similarities between gravitomagnetism and electromagnetism: $M_G={\frac {1}{2}}\iiint _{V}\mathbf {r} \times \mathbf {j} \,{\rm {d}}V$
$|M_G|={\frac {1}{2}}\iiint _{V}r \frac{d^2m}{dl dt} dV=\frac {1}{2}\iiint _{V}r \rho v dV=\frac {1}{2}\int_V r^2 \rho \omega dV=\frac {1}{2}\int_{R_1}^{R_2}h r^2 \rho \omega 2\pi r dr=\frac {h \rho \omega 2\pi}{2}\int_{R_1}^{R_2}(r^3 dr)=\frac{2\pi \rho (R_2^4-R_1^4) h \omega_2}{8}=\frac{2\pi\rho(R_2^4-R_1^4)h\omega_2}{8}$.

torque:
I used formula $\tau=M\times B$ from https://en.wikipedia.org/wiki/Magnetic_moment
using similarities between gravitomagnetism and electromagnetism: $\tau=4 M_G\times B_G$

 

[olgerm]

What youyhink what would the highest $\rho$ and $\omega$ values practically possible?

 

[PeterDonis]

What youyhink what would the highest ρ\rho and ω\omega values practically possible?

What do you think? Have you looked up properties of any materials you might use, like density and tensile strength? Have you calculated what the stress in the material would be at various rotational frequencies?

 

[Vanadium 50]

highest value for τ

How long is a piece of string?

Clearly the smallest torque you could measure on a watchspring is smaller than the smallest torque you could measure on a planet.

 

[Ibix]

Much more readable than last time, thank you. However, note that this is incorrect

$\mu_G$is gravitomagnetic constant ##\mu_G=\frac{2 2\pi G}{c^2} \approx 9.33\ 10^{-27}N/kg^2s^2

It should be $\mu_G=4\pi G/c^2\approx 9.33\times 10^{-27}\mathrm{N kg^{-2}s^2}$. And some use of the paragraph maths mode ($$ instead of ##) and the eqnarray environment would also help. So instead of this

$|M_G|={\frac {1}{2}}\iiint _{V}r \frac{d^2m}{dl dt} dV=\frac {1}{2}\iiint _{V}r \rho v dV=\frac {1}{2}\int_V r^2 \rho \omega dV=\frac {1}{2}\int_{R_1}^{R_2}h r^2 \rho \omega 2\pi r dr=\frac {h \rho \omega 2\pi}{2}\int_{R_1}^{R_2}(r^3 dr)=\frac{2\pi \rho (R_2^4-R_1^4) h \omega_2}{8}=\frac{2\pi\rho(R_2^4-R_1^4)h\omega_2}{8}$

you get$$\begin{eqnarray}
|M_G|&=&{\frac {1}{2}}\iiint _{V}r \frac{d^2m}{dl dt} dV\\
&=&\frac {1}{2}\iiint _{V}r \rho v dV\\
&=&\frac {1}{2}\int_V r^2 \rho \omega dV\\
&=&\frac {1}{2}\int_{R_1}^{R_2}h r^2 \rho \omega 2\pi r dr\\
&=&\frac {h \rho \omega 2\pi}{2}\int_{R_1}^{R_2}(r^3 dr)\\
&=&\frac{2\pi \rho (R_2^4-R_1^4) h \omega_2}{8}\\
&=&\frac{2\pi\rho(R_2^4-R_1^4)h\omega_2}{8}
\end{eqnarray}$$

I haven't had a chance to think about the details of what you wrote - I will have a look. Obvious comments given what we worked out last time are that you are assuming that your cylinders are infinitely long and that your small cylinder is infinitely small in an infinitely narrow gap between the two cylinders. How sensitive is your maths to the lack of infinities in reality?

 

[Ibix]

As I noted, you need to think about the field from a pair of finite cylinders with a finite separation. That'll get you a revised $B_G$ and hence a revised expression for $\tau$. Incidentally, where did the 4 come from in the last expression in your OP?

But this new $\tau$ will depend on a lot of variables - $\rho_1$, $r_1$, $r_2$, $L$ (the length of cylinders 1 and 2), $\delta$ (half the gap between cylinders 1 and 2), $\omega_1$, $\rho_3$, $R_1$, $R_2$, $h$, and $\omega_2$. You need to constrain these somehow. A few constraints are easy:

• At least for a first pass I'd set $r_1=R_1=0$.
• You can set $R_2=\delta$, so the perpendicular cylinder fits exactly between the co-axial ones - don't worry about clearances at this stage.
• Unless you want to go into details of the off-axis field, I'd just require $h\ll 2r_2$ - maybe set $h=r_2/2$.

A more complex constraint is that you don't want your cylinders to disintegrate. You need to look at the stresses in a spinning cylinder (Google is your friend) and require that they be below the yield stress of the material. That'll give you an expression for you $\omega$s in terms of the sizes, densities, and yield stresses of your cylinders.

Then you just play around. Look up some material densities and yield stresses and plug them in. That should mean that you now have an expression for $\tau$ in terms of just three variables $r_2$, $L$, $R_2$. You can add another constraint by insisting that the volumes of the cylinders are some constant determined by your budget for buying materials - so now you have a function of only two variables (times a few different materials). Plug a range of values in and see if you can find the combination that gives you the best $\tau$ - optimisation algorithms will help, but you could just brute force it.

Optionally, you could plug in a maximum energy for spinning the cylinders, which would limit the range of cylinder sizes possible given your rotation rate. If you don't do that, definitely check that you don't have stupid energy requirements!

That'd be my approach, anyway. Then you could see what kind of $\tau$s you can actually generate on cylinders of known mass, and we can think about whether detecting them is plausible at all.

 

[olgerm]

As I noted, you need to think about the field from a pair of finite cylinders with a finite separation.

For simplicity I assuma that 1. and 2. cylinders are much larger than 3. cylinder.

How sensitive is your maths to the lack of infinities in reality=

Not very sensitive.

 

[olgerm]

What do you think? Have you looked up properties of any materials you might use, like density and tensile strength? Have you calculated what the stress in the material would be at various rotational frequencies?

I do not know for sure how to calculate maximum rotational speed from tensile strength. Maybe someone who has some experience could give me order of magnitude.

 

[berkeman]

I do not know for sure how to calculate maximum rotational speed from tensile strength. Maybe someone who has some experience could give me order of magnitude.

https://en.wikipedia.org/wiki/Flywheel_energy_storage

 

[Nugatory]

I do not know for sure how to calculate maximum rotational speed from tensile strength. Maybe someone who has some experience could give me order of magnitude.

I won’t do that, but I will tell you how to arrive at such an estimate for yourself.

consider a small volume at the edge of the cylinder, surface area $dA$ and thickness $dR$. What is its volume and mass? What is the radial acceleration needed to keep it on its circular path? What force is needed to produce that acceleration? That force is more or less evenly distributed across the surface area... you can take it from here

 

[Ibix]

For simplicity I assuma that 1. and 2. cylinders are much larger than 3. cylinder.

Ok. But your torque depends on $R_2^4$. Insisting that $R_2$ be small seems like a mistake to me.

Not very sensitive.

Perhaps you could show your maths for this? My quick calculation suggests that for a fixed mass of metal I can get an order of magnitude variation in $B_G$ by varying the aspect ratio of the cylinders.

 

[olgerm]

https://en.wikipedia.org/wiki/Flywheel_energy_storage

${\displaystyle {\frac {E}{I}}=K\left({\frac {\sigma }{\rho }}\right),}$ is not helpful because it is about kinetic energy not generated GM-field.

$B_G=\frac{\mu_G \rho \omega (r_2^2-r_1^2)}{2}$, but
$E_{kinetic}=\frac{\rho\ \omega^2\ 2\pi (r_2^4-r_1^4)\ h}{8}$

B_G is proptional to $r^2$, but kinetic energy is propotional to $r^4$.

 

[olgerm]

Perhaps you could show your maths for this?

It is analogues to electromagneism where big solenoid creates homogeneous magnetic field near its ends. (https://en.wikipedia.org/wiki/Solenoid#Quantitative_description)

 

[Ibix]

it is about kinetic energy

And rotational kinetic energy depends on...

 

[Vanadium 50]

On top of everything else, I am not sure that conceptually this is correct. Which way does the third cylinder want to rotate? And why?

(If you say "because of the right-hand rule" as part of your answer, my next question is "and where does that come out of GR?")

 

[olgerm]

And rotational kinetic energy depends on...

You mean $\frac{E}{I}=\frac{\omega^2}{2}$
so $\omega=\sqrt{\frac{2\ K\ \sigma}{\rho}}$?
It seems wrongbeacause omega does no depend of r.
Could you just write correct expression for maximum $\omega\ r^2$?

 

[olgerm]

Which way does the third cylinder want to rotate? And why?

because of the right-hand rule. I use Gravitoelectromagnetic model, which is approximation for GR where gravitational fields are small.

 

[PeterDonis]

because of the right-hand rule.

As @Vanadium 50 was hinting in post #15, a human choice of convention for how to represent things, which is what the right hand rule is, cannot have a physical effect. So this answer cannot be correct. The right-hand rule can't make things rotate a certain way.

 

[Ibix]

It seems wrongbeacause omega does no depend of r.

Good point - that does seem odd. You could check another source, or you could work through Nugatory's method (which was more or less what I had in mind when I proposed this above).

Could you just write correct expression for maximum $\omega\ r^2$?

No, because I haven't worked through the maths myself. Happy to check yours when you've done it.

 

[Vanadium 50]

which is approximation for GR where gravitational fields are small.

Articles are important. It is an approximation, not the approximation.

I am not convinced this is a valid approximation. I'd want to see an explanation for the direction that Cylinder 3 turns.

 

[Vanadium 50]

Which way does the third cylinder want to rotate? And why?

If you say "because of the right-hand rule" as part of your answer, my next question is "and where does that come out of GR?"

because of the right-hand rule

I didn't think I'd need to say this, but OK, "where does that come out of GR?"

 

[Ibix]

I am not convinced this is a valid approximation. I'd want to see an explanation for the direction that Cyliner 3 turns.

Depends on the sense of rotation of cylinders 1/2 and 3, I think. You could look at pairs of ingoing and outgoing geodesics near the pole of a Kerr black hole, I guess?

I'm also slightly concerned that this is applying a non-coaxial torque to a spinning cylinder - i.e. a gyroscope. In other words you'd need to look for precession, which is likely to look very like vibration from the spinning...

 

[Vanadium 50]

I'd like to know where it comes from.

What I suspect is happening is that the rotation causes terms to cancel at first order (for every mass element moving at v, there is one moving at -v) so the terms we neglected in getting to geomanetism become important. But let's start with the simpler question: clockwise or counter-clockwise.

 

[Vanadium 50]

And for extra fun, if I reverse all three spins, which way does it rotate?

 

[olgerm]

And for extra fun, if I reverse all three spins, which way does it rotate?

Torque on 3. cylinder is crosswise to angular speeds of 1. , 2. and 3. cylinder.

$\tau=4 M_G\times B_G$
$|\tau|=\frac{2\pi \rho_3 (R_2^4-R_1^4) \omega_3 B_G}{2}=\frac{\mu_G \omega_3 \rho_3 (r_2^2-r_1^2) 2\pi \rho_1 (R_2^4-R_1^4) \omega_1}{4}$

What I suspect is happening is that the rotation causes terms to cancel at first order (for every mass element moving at v, there is one moving at -v)

No, because opposite moving sides have opposite displacement from centre. Same way that solenoid magnetic field is not canceling out altougth there are opposite current on different sides from centre.

 

[Ibix]

What I suspect is happening is that the rotation causes terms to cancel at first order (for every mass element moving at v, there is one moving at -v) so the terms we neglected in getting to geomanetism become important. But let's start with the simpler question: clockwise or counter-clockwise.

I guess I don't understand your objection here. Gravitomagnetism certainly seems to predict that the third cylinder will attempt to rotate - the "magnetic" field of the two coaxial cylinders is parallel to their axis and the "magnetic moment" of the third cylinder is perpendicular to that, which produces a torque perpendicular to the plane defined by the cylinder axes, and hence rotation in that plane. Which way it goes I don't know without keeping track of signs which I haven't bothered to do, but I'm not sure what doing so would add. Here's a sketch of my understanding - red arrows represent the spins of the cylinders and green the "magnetically" induced rotation of the small cylinder:

As noted I haven't checked the signs of the rotations for consistency, and the small cylinder is a gyroscope so it'll start to precess rather than rotate steadily in that plane - but I think that's how this model says it'll start moving. I'd expect changing the sense of the rotations of the large cylinders or the small cylinder to reverse the sense of the green arrow; reversing both would leave the green arrow unchanged. Or am I missing something?

I admit I haven't seen a derivation of gravitomagnetism from the EFEs - my quick reading has only provided a derivation by blunt assertion (Newtonian gravity looks like a Coulomb field so perhaps there's a gravitational analogue for the magnetic field - originally a proposal by Heaviside, I think).

 

[pervect]

Derivation of equations
gravitimagneticfield:
I used formula $B=\mu n I$ from http://hyperphysics.phy-astr.gsu.edu/hbase/magnetic/solenoid.html.

I see no reason why this formula should be correct for a solid cylinder. You assume the field is the same as a soleniod for no reason that you've explained, logically.

That formula also doesn't seem to match the Wiki's formula for the gravitomagnetic field of a rotating body. See for instance https://en.wikipedia.org/w/index.ph...ravitomagnetic_fields_of_astronomical_objects.

Wiki's formula does not have a reference, unfortunately, so it may be incorrect too.

I'm a bit unclear why you need or want three cylinders. Your diagram isn't really clear to me, reverse engineering of what I think you should be doing suggests two cylinders should be enough.

[add] Ibix's 3d diagram seems clear, if that's what you're suggesting, I don't see the need for three cylinders.

One cylinder is needed to generate the gravitomagnetic field, the second is redundant. A second is needed to measure the torque. But your diagram isn't clear enough that I'm confident that you're doing what I think you should be doing.

Note that the torque will be proportioanl to the mass, so what you're really looking for is the precession of a gyroscope caused by the gravitomagnetic field.

Gravity Probe B already has done a test of gravitomagnetism. So I'd suggest looking at the GP-B experiment rather than trying to create your own. Their test is rather similar to the 2-body version of the test I think you are suggesting, omitting the third unecessary body. There's a brief overview of GP-B at

https://einstein.stanford.edu/content/fact_sheet/GP-B_Nutshell-0307.pdf has a summary.

I won't get into the results of GP-B, except that it was felt that the experiment did confirm gravitomagnetism, in spite of some unexpected experimentally glitches with their gyroscopes having less than ideal behavior.

The first thing you might want to think about motivationally is whether or not you can create a gravitomagnetic field in a lab that's stronger than that produced by the rotating Earth. You'll need a convicing formula for the field in order to do that - I am simply not conviced that your use of the solenoid as a an exemplar is correct.

As I suggested earlier, you also need reasonable physical limits on your spining bodies - bodies that spin so fast that they'd fail to hold together are not a reasonable test candidate.

So in summary, I expect that something vaguely similar to what you're proposing has already been done, Namely GP-B, and it has already confirmed the existence of gravitomagnetism.

 

[Vanadium 50]

I guess I don't understand your objection here.

The objection is that I am not sure the gravitomagnetism approximation is correct here.

[A-level digression]The "right-hand rule" or a "cross-product" is a statement of an anti-symmetric tensor in the problem. In EM and GR these come in different places: the Faraday tensor is intrinsically anti-symmetric, where in GR it comes in as the anti-symmetric piece of the Lense-Thirring metric. There is no reason to believe that these lead to the same result.[/A-level digression]

Because this thread (and its predecessor) involved tossing equations and values around willy-nilly, it's not clear that the rationale leading to gravitomagnetism applies here. In gravitomagetism, one says "I have a particle of mass m and velocity v. If I want a Lorentz-invarient theory, I need a Lorentz-like force on this particle, so I need a 'gravitomagnetic field'. All other terms are small and can be dropped."

That is not the case we have here. Linear momentum is zero. Linear momentum on one side of the cylinder is canceled by the opposite linear momentum on the other. It may be that the expression is still correct (or maybe off by a factor of 2 or something) but it is far from guaranteed. The "large" term is zero, and the effect is from the "small" terms.

An order-of-magnitude guess is that since this is second order in v (e.g. L²/2I), the size of the effect relative to Newtonian gravity is ~β². If the cylinder surfaces are moving at 1000 mph, the effect is a few x 10^-12.

 

[Vanadium 50]

The question about reversals is an attempt to tease out the parity properties.

Let's assume Cylinder 3 rotates clockwise in the green direction.

If I reverse the spin of the big cylinders, the rotation becomes CCW. Now reverse the spin of the small cylinder, and it's CW again. It looks to me like a parity-odd transformation, which is a peculiar outcome from a parity-conserving theory.

 

[olgerm]

I would like to getestimation on maximum $\tau$ and $B_G$. For that I need maximum $\omega_1\ \ \rho_1\ (r_2^2-r_1^2)$ and maximum $\omega_3\ \rho_1\ (R_2^4-R_1^4)$.

Do you think $\omega=\sqrt{\frac{2\ K\ \sigma}{\rho}}$ is correct?
if it is then
$|\tau|=\frac{2\pi \rho_3 (R_2^4-R_1^4) \omega_3 B_G}{2}=\frac{\mu_G \omega_3 \rho_3 (r_2^2-r_1^2) 2\pi \rho_1 (R_2^4-R_1^4) \omega_1}{4}=\frac{2\ K\ \sigma\ \mu_G\ (r_2^2-r_1^2) 2\pi\ (R_2^4-R_1^4)}{4}$

 

[olgerm]

consider a small volume at the edge of the cylinder, surface area $dA$ and thickness $dR$. What is its volume and mass? What is the radial acceleration needed to keep it on its circular path? What force is needed to produce that acceleration? That force is more or less evenly distributed across the surface area... you can take it from here

it is $\omega^2\ R\ \rho\ dR\ dA$?

 

[pervect]

A few comments based on my understanding of GP-B, and Ibix's diagram:

The two parallel spinning cylinders crate a gravitomagnetic field. There's no real reason we actually need two of them. One rotating cylinder is sufficient to create the gravitomagentic field. Let's remove the cylinder on the right.

Then the large cylinder on the left is equivalent to the rotating Earth, and the small rotating stick, the test intsturment, is equivalent to the GP-B satellite, in a polar orbit around the Earth.

For GP-B, we do not measure the torque on the small spinning cylinder directly, instead we insure that there are no external torques on the test gyroscope other than due to the gravitomagnetic effect, and observe its rate of precession. The gravitomagnetic torque on the spinning test gyroscope causes it to precess, and we observe the precession. Ensuring there are no extraneous sources of torque isn't particularly easy to the required level of accuracy, however I don't recall exactly what precautions needed to be taken for GP-B.

The equations that govern the behavior of the torque-free motion of the spinning rod are Euler's equations. [wiki link].

These equations will be greatly simplified if the rotating body is a sphere rather than a cylinder, which is what was done in GP-B.

As I recall, neither the mass, density, nor the rate of angular rotation omega of the test gyroscope matters to the end result. A more massive gyroscope will generate more torque, but it will precess less due to it's larger mass. Similarly, spinning up the gyroscope to a higher value of omega will increase the torque, but it will not affect the rate of precession. It's fairly obvious that the mass or size shouldn't affect the precession rate. Proving that it's independent of omega as well should be possible from Euler's equations, but I haven't done so.

 

[Vanadium 50]

For GP-B, we do not measure the torque on the small spinning cylinder directly, instead we insure that there are no external torques on the test gyroscope other than due to the gravitomagnetic effect, and observe its rate of precession.

Which was one rotation per 30 million years. Not a big effect (and Gravity Probe B had a lot of trouble measuring it).

This lines up with my ballpark β² estimate. Say orbinal speed is 17000 miles per hour and the Earth rotation is 1000. So it's about a 4 x 10^-11 effect. One turn per 30 million years is a part in 10¹¹.

 

[Nugatory]

it is $\omega^2\ R\ \rho\ dR\ dA$?

Yes, that is the necessary force.

 

[Ibix]

I've been doing a bit of reading on gravitoelectromagnetism.

As @pervect noted in #27, the formula for the gravitomagnetic field, $B_G$, given in the Wikipedia page on gravitomagnetism is $$B_G=\frac{G}{2c^2}\frac{\vec L-3(\vec L.\vec r)\vec r/r^2}{r^3}$$This does not match the formula in the OP. Following a hint from @Vanadium 50 I found this Wikipedia page which has a "fill in the blanks" derivation of the gravitoelectromagnetic equations and hence the formula quoted above starting from the Lense-Thirring metric. This at least cites a source for the metric - MTW chapter 19, and we do indeed find the Lense-Thirring metric there (MTW equation 19.5). But it's different from the one on Wikipedia in that it shows the order of the terms that get dropped in the approximation, which include terms of order $1/r^3$, where $r$ is the distance from the center of mass of the spinning object.

On that basis (and I'm open to correction here!) it looks to me like gravitoelectromagnetism is inappropriate for the scenario proposed by @olgerm, since the "sensor" cylinder is bang on the center of mass of the "generator" cylinders. The extra terms would be non-negligible so the various elements of $h_{\mu\nu}$ no longer look like $\phi$ and $\vec{A}$. That objection doesn't necessarily apply to pervect's revised version, which has the sensor cylinder away from the center of mass of the generator cylinder. You'd actually want to do MTW's exercise 19.1 to get the form of the allegedly negligible terms to confirm that (MTW are also fans of letting you fill in the blanks in their derivations).

Edit: Further, MTW note that Lense-Thirring assumes that the self-gravity of the spinning object is negligible, which would apply to the finite cylinders I drew but not the infinite length cylinder OP assumes.

But that still leaves the question of why Wikipedia's formula for $B_G$ doesn't match the OP's. I have a possible suggestion for that - the Lense-Thirring metric seems to be specified in isotropic coordinates in order to get a simple equivalence with Maxwell's equations. So wouldn't we have to specify the mass current density in those same coordinates to be able to apply standard results from electromagnetism? I don't think that happened.

 

[olgerm]

$dF=\omega^2\ R\ \rho\ dR\ dA$

Yes, that is the necessary force.

How to calculate maximum $\omega$ from this?

$dF=dA\ \sigma$ and therefore
$dA\ \sigma=\omega^2\ R\ \rho\ dR\ dA$
$\sigma=\omega^2\ R\ \rho\ dR$
$\omega=\sqrt{\frac{\sigma}{R\ \rho\ dR}}$
that can't be right because $dR$ remains in. What the correct way for calculating max $\omega$?

 

[pervect]

Which was one rotation per 30 million years. Not a big effect (and Gravity Probe B had a lot of trouble measuring it).

This lines up with my ballpark β² estimate. Say orbinal speed is 17000 miles per hour and the Earth rotation is 1000. So it's about a 4 x 10^-11 effect. One turn per 30 million years is a part in 10¹¹.

For the record, I also very much doubt that a lab experiment is going to be able to replicate the GP-B results. I do think that the effort to investigate other approaches could be of educational benefit if done correctly and methodically. The primary benefit and onus of such investigation is on the poster. An important part of the investigation process is to read as much of the relevant literature as one is able, to see what others have done previously, and to be on the lookout for things that don't quite fit.

 

[Vanadium 50]

The primary benefit and onus of such investigation is on the poster. An important part of the investigation process is to read as much of the relevant literature as one is able, to see what others have done previously, and to be on the lookout for things that don't quite fit.

I see very little of that from the OP. He keeps asking us the same questions over and over and not addressing any of the issues we have brought up. In fact, I found a thread of his from five years ago where we are covering the same issues. Including the suggestion that he look at Gravity Probe B. Not much seems to have come from that.

 

[olgerm]

]Do you think $\omega=\sqrt{\frac{2\ K\ \sigma}{\rho}}$ is correct?
if it is then
$|\tau|=\frac{2\pi \rho_3 (R_2^4-R_1^4) \omega_3 B_G}{2}=\frac{\mu_G \omega_3 \rho_3 (r_2^2-r_1^2) 2\pi \rho_1 (R_2^4-R_1^4) \omega_1}{4}=\frac{2\ K\ \sigma\ \mu_G\ (r_2^2-r_1^2) 2\pi\ (R_2^4-R_1^4)}{4}$

if I assume it is correct:
$\mu_G=\frac{2\ 2\pi\ G}{c^2} \approx 9.33\ 10^{-27}\ N\ s^2/kg^2$
$K=0.5$
$\sigma=7000000000\ Pa$
$r_2=5$
$r_1=0$
$R_2=1$
$R_1=0$
$|\tau|=\frac{2\ K\ \sigma\ \mu_G\ (r_2^2-r_1^2) 2\pi\ (R_2^4-R_1^4)}{4}=2.57\ 10^{-15}\ N\ m$

Do you agree, that making this assumation my result is correct? Do you agree, that this effect is too small to be measured?
Do you think the assumation is correct?

 

[Nugatory]

that can't be right because $dR$ remains in.

A differential that you can’t get rid of is telling you that there’s an integral in your future.

 

[olgerm]

A differential that you can’t get rid of is telling you that there’s an integral in your future.

Should I integrate this side over R?

 

[Nugatory]

Should I integrate this side over R?

if you choose the right bounds of integration you will have the quantity that you will compare with the tensile strength

 

[pervect]

Here is a sketch of my argument that a large rotating object, such as the Earth, is going to be a stronger source of the gravitomagnetic field than a smaller, lab-created object.

The significance of this is that it's very hard to test for the existence of the gravitomagnetic filed of the Earth (though, as has been mentioned, it has been done) - thus, trying to do it in a pure lab envirnoment will be more difficult and probably impossible.

To start with, we need to know the basics dimensional dependency of the gravitomagnetic field. Neglecting all the various numerical factors, we find from the examples in Wiki that at the surface of a spherical body of radius R, the gravitomagnetic field strength will be proportional to

$$B_G \propto \frac{G}{c^2} \frac{m}{R} \, \omega\propto \frac{G}{c^2} \rho \, R^2 \, \omega \propto \frac{G}{c^2} \, \rho \, V^2 / \omega$$

here G is the gravitational constant and c is the speed of light - not strictly necessary to include, as they are constants, but they make the units sensible. R is the radius of the sphere, $\omega$ is it's rate of rotation, and V = $r \omega$ is the surface velocity of the sphere.

The significance of using V is that for any given material, a hoop of that material held together only by it's own strength (and not gravity) has a maximum tangential velocity before it will fail under stress. Gravity becomes important for larger objects, but for lab scale objects, this characteristic velocity is what's useful. While we are using a sphere and not a hoop, I think the failure criterion for a rotating sphere would be similar, though it would certainly be better to do a more thourough analysis.

The source of the observation about the importance of V is from the wiki page on space tethers, https://en.wikipedia.org/w/index.ph...ldid=953929239#Properties_of_useful_materials

Hypersonic skyhook equations use the material's "specific velocity" which is equal to the maximum tangential velocity a spinning hoop can attain without breaking:

From the same article, we can see that the maximum known theoretical characteristic velocity would be for single walled carbon walled nanotubes, of about 5 km/sec, with commercially available materials (single walled carbon nanotubes are not yet commerically available in usable form AFAIK) being as high as 2km/sec.

So, where does the Earth fit on this scale? The velocity at the surface of the Earth is small, so V = .5 km/sec, about 1/10 of the maximum value of V we can get in a lab. So, potentailly, the lab could be better based solely on V. However, the field stregnth is proportioanl to $V^2 / \omega$, and $\omega$ is very small for the Earth, making it the better candidate. Basically, the fact that the field strength is inversely proportional to $\omega$ tells us that larger structures, even though they rotate at a slower angular velocity $\omega$ will produce a larger gravitomagnetic field than small, faster rotating structures.

Since the Earth is already here, it's an ideal candidate for the source of the field. Perhaps another astronomical object would be even better, but the Earth is convenient because it's so nearby.

The remaining issue is how to detect the field. Measuring the torque directly would require bearings that can hold the axis of rotation stable with unreasonable accuarcy levels, and have a significant potential for introducing errors. So observing the precession directly, rather than trying to hold the direction stable and measure the force, seems far preferable. The question remains as to why an orbital approach is the best approach, rather than some surface mounted experiment. My thoughts on this are that eliminating effects due to Thomas precession , https://en.wikipedia.org/wiki/Thomas_precession, was the motivation for having the measuring instrument be in free fall, which implies an orbital experiment as opposed to a surface based experiment.

So in conclusion, larger is better as far as generating a gravitomagnetic field, and there isn't any obvious choice for a better detection scheme of said field than the GP-B satelite system - which was up to the job, but just barely.

 

[olgerm]

if you choose the right bounds of integration you will have the quantity that you will compare with the tensile strength

I still do not know how to do it. Could you just solve it for maximum angular speed?

 

[Vanadium 50]

@pervect, I like the analysis. However, there is a difference between angular momentum GR effects and gravitomagnetism, which is one particular angular momentum GR effect. Given that the OP has not commented on any of the fundamental issues that have been brought up, it's not clear what his reaction will be.

Dimensional analysis like yours shows the effect is of order β² or in more detail, β₁ x β₂. The real power of Gravity Probe B is that it's in orbit: so you have a velocity of 17000 mph there - 17x faster than the Earth's rotation. Gravity Probe B needed that factor of 17.

The perigee advance - the equivalent of Mercury's perihelion advance - was measured to be about 15x larger than Mercury's. Mercury advances more per orbit, but a LEO satellite makes many more orbits.

 

[Nugatory]

I still do not know how to do it. Could you just solve it for maximum angular speed?

To do that you need the stress as a function of the angular speed. So far you have the force needed to keep a segment of thickness $dr$ at a distance $r$ from the axis on its circular path. The radial stress at a distance $r$ from the center must be sufficient to keep every segment between $r$ and the outer edge on its circular path.

(Of course we’re trying to come up with an order of magnitude estimate here. We’re neglecting tangential stresses, and if the outer rim is moving at relativistic speeds this calculation is going to be waaay optimistic... but it will quickly tell you whether any reasonable material can come close to the sort of rotational velocity you need)

 

[olgerm]

To do that you need the stress as a function of the angular speed.

Is that correct $\sigma=\int_{r_1}^{r_2}(\omega^2\ R\ \rho\ dR)=(r_1^2-r_2^2)\ \omega^2\ \rho$?

 

[Nugatory]

Is that correct $\sigma=\int_{r_1}^{r_2}(\omega^2\ R\ \rho\ dR)=(r_1^2-r_2^2)\ \omega^2\ \rho$?

You have two arithmetic errors in the integral you did (missing a factor of 1/2 and the wrong sign), both easily correctable. But the integral still isn’t right because $dA$ is not constant, it’s a function of $r$.

 

[olgerm]

a large rotating object, such as the Earth, is going to be a stronger source of the gravitomagnetic field than a smaller, lab-created object.

how big is $B_{G\ Earth}$and how big is $B_{G\ lab}$?

 

[pervect]

how big is $B_{G\ Earth}$and how big is $B_{G\ lab}$?

It depends on the size of the rotating object in the lab. The argument basically says the bigger the object the better.

I can give you a more detailed answer if you give me figures for $\rho$, $V$, and $R$ for your version of the lab experiment. $\rho$ and V can both be estimated from what material you chose to make your lab mass out of.

The TL;DR (too long, didn't read) answer is that you'd need a lab sphere with a radius of at least 120 km to get a $B_G$ comparable to that of the Earth.

The basic formula is simple, though.

$$B_G = (some-constant) * \frac{G}{c^2} \rho \, V \, R$$

This is slightly modified (and clearer) than the expression in my original post. Here $\rho$ is the density, V = $R \omega$ is the tangential velocity of the sphere, ($\omega$ being the angular velocity of the sphere) and R is the radius of the sphere.

We don't need to know the value of the constant to compare identically shaped rotating sources. Since the Earth is roughly spherical, I am assuming that the lab source is also spherical to make the sources more comparable. You might pick up some small advantage (or potentially a disadvantage) for other shapes for your source, such as your favorite cylinder, but it probably won't be a huge advantage.

Since V for the Earth is .5 km / second, and the best plausible materials would be under 5 km/sec, you might get a factor of up to 10 with the right material. V is limited by the constraint that your rotating test mass doesn't fail due to internal stresses. See the article previously referenced on space tethers for where the requirement for limiting V, the tangential velocity, came from.

Hypersonic skyhook equations use the material's "specific velocity" which is equal to the maximum tangential velocity a spinning hoop can attain without breaking:

$$ V = \sqrt{\frac{\sigma}{\rho}}$$

$\sigma$ is the stress limit of your material, and $\rho$ is it's density. The equation is not for a rotating sphere, but for a rotating hoop, so it's only an estimate.

You probably won't get a density $\rho$ more than 5 times that of the Earth. So, optimistically, assuming you could both get high density and high V in the same material (unlikely), your lab mass would need to be 1/50 the radius of the Earth to have the same gravitomagnetic field. And that's being very optimistic, a better analysis would probably show that the required radius would be much larger.

Since the Earth's radius is about 6000 km, you'd be talking about your lab mass being a sphere 120 km in diameter to get a comparable field. And this is just silly when the Earth's field is free. Also, if you are doing your experiment on the Earth, its field would affect your result anyway, unless you took pains to elimiante it. But there's no sensible reason to try and elimiante the contribution of the Earth gravitomagnetic field rather than to take advantage of it.