Mitchell Powell
- 4
- 0
Homework Statement
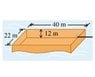
An open barge has the dimensions shown in the figure.
https://physicsforums-bernhardtmediall.netdna-ssl.com/data/attachments/59/59574-46462a33e8dd3e05fa12094d99749d9c.jpg
If the barge is made out of 5.2-cm-thick steel plate on each of its four sides and its bottom, what mass of coal can the barge carry in freshwater without sinking?
Homework Equations
p = m/V
The Attempt at a Solution
V = 22 * 40 * 12 m3 = 10,560 m3
pwater = 1,000 kg/m3
1,000 kg/m3 = m/10,560
m = 1,000*10,560 = 10,560,000 kg
Attachments
Last edited by a moderator: