Car passing a truck — calculating the relative motions

[rssvn]

Homework Statement

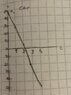
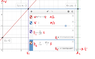
Car drives a straight road at 20m/s, a truck is driving at 18m/s infront of the car. When the car is 50 m behind the truck, it starts to pass the truck with constant acceleration of 1.8m/s^2 until it hits the speedlimit of 25m/s, after that the car continues driving with the speed of 25m/s.
a) How far has the car gone during the acceleration?
b) How far did the car get when the front of the car was next to the front of the truck, start from the beginning of the acceleratoion.

Relevant Equations

vf=vi+at , vf^2=vo^2+2a(xf-xo)

The question was translated from finnish so apologies if everything doesn't make sense:) and please do tell if the equations are wrong.

 

[berkeman]

Welcome to PhysicsForums.

Can you make a sketch of the position of each vehicle versus time and upload it? That would help us to get you started on the problem. Use the "Attach files" link below the Edit window to upload a PDF or JPEG copy of your sketch. We need to see your best efforts to start working the problem before we can offer tutorial help. Thanks.

 

[haruspex]

The question was translated from finnish so apologies if everything doesn't make sense:) and please do tell if the equations are wrong.

The question is clear and makes sense.
The equations look ok, but equations can only really be judged when all the variables are defined and all the assumptions stated.
The test will be in how you apply them. We look forward to seeing that.

 

[rssvn]

Here are 2 quick graphs i made, please let me know if they are not sufficient :)

 

[PeroK]

Here are 2 quick graphs i made, please let me know if they are not sufficient :)

I'm not sure those help you very much. The car accelerates for a time, so its distance vs time graph should be curved.

In any case, have you made any progress with the calculations?

 

[haruspex]

Let's start with this piece:
"Car drives a straight road at 20m/s ... constant acceleration of 1.8m/s^2 until it hits the speedlimit of 25m/s."
How long does that take and how far has the car travelled?

 

[rssvn]

2.8 s to reach 25m/s and 90.4m? and thank you all for helping! :)

 

[haruspex]

2.8 s to reach 25m/s and 90.4m? and thank you all for helping! :)

2.8s, yes (though I wouid keep a bit more precision at this stage), but how do you get 90.4m?

 

[rssvn]

I meant 70.4 :) i added 1.8 m/s to the initial 20m/s for 2.8 times

 

[haruspex]

I meant 70.4

Still too much. What is the average speed during the constant acceleration?

i added 1.8 m/s to the initial 20m/s for 2.8 times

I hope what you mean is that you added 1.8m/s² for time t to the initial 20m/s to get to 25m/s.

 

[rssvn]

Still too much. What is the average speed during the constant acceleration?

I hope what you mean is that you added 1.8m/s² for time t to the initial 20m/s to get to 25m/s.

Yes, sorry didnt know how to write it correctly :) and average speed 22.5m/s

 

[PeroK]

2.8 s to reach 25m/s and 90.4m? and thank you all for helping! :)

According to my calculator $5/1.8 = 2.777 \dots$, so I'd use $t = \frac{25}{9} s$.

 

[haruspex]

Yes, sorry didnt know how to write it correctly :) and average speed 22.5m/s

Yes, 22.5m/s average for 2.78s. So what distance is covered?

 

[rssvn]

According to my calculator $5/1.8 = 2.777 \dots$, so I'd use $t = \frac{25}{9} s$.

how did you get 25/9?

Yes, 22.5m/s average for 2.78s. So what distance is covered?

62.55 m

 

[haruspex]

how did you get 25/9?62.55 m

Yes. But I strongly encourage you to resist plugging in numbers until the end for any given answer. It has many advantages.
E.g. if you had written $v_f=v_i+at$ and $s=(v_i+v_f)t/2$ you would have arrived at $s=\frac{v_f^2-v_i^2}{2a}=62.5m$ exactly.

Next, where is the car in relation to the truck at the end of the acceleration?

 

[rssvn]

Yes. But I strongly encourage you to resist plugging in numbers until the end for any given answer. It has many advantages.
E.g. if you had written $v_f=v_i+at$ and $s=(v_i+v_f)t/2$ you would have arrived at $s=\frac{v_f^2-v_i^2}{2a}=62.5m$ exactly.

Next, where is the car in relation to the truck at the end of the acceleration?

Ah, i had been counting xo as 50m in the second equation.

the car is at the rear of the truck?

 

[haruspex]

the car is at the rear of the truck?

There's no reason to suppose that.
You know what the relative positions were at the start of the acceleration, and you know how far the car went during the acceleration and how long that took. So how do you work out the relative position at the end of the acceleration?

 

[PeroK]

how did you get 25/9?

$5/1.8 = 25/9$

So, I can check your answer for distance:
$$(\frac {25} 9 s) \times (22.5 m/s) = (\frac {25} 9) \times (\frac {45} 2)m = 25 \times (\frac 5 2)m = \frac{125}{2}m = 62.5m$$ With no rounding errors!

Perhaps you don't get taught this sort of thing in schools anymore? In any case, if you put $22.5 \times 5 / 1.8$ into a calculator you'll get an exact answer.

Try using the $25/9 \ s$ or $5/1.8 \ s$ to calculate where the truck is when the car stops accelerating. Is that better than using $2.78s$?

 

[rssvn]

There's no reason to suppose that.
You know what the relative positions were at the start of the acceleration, and you know how far the car went during the acceleration and how long that took. So how do you work out the relative position at the end of the acceleration?

if the truck went 50m in 2.78s and the car went 62.55m it must be still behind the truck

$5/1.8 = 25/9$

So, I can check your answer for distance:
$$(\frac {25} 9 s) \times (22.5 m/s) = (\frac {25} 9) \times (\frac {45} 2)m = 25 \times (\frac 5 2)m = \frac{125}{2}m = 62.5m$$ With no rounding errors!

Perhaps you don't get taught this sort of thing in schools anymore? In any case, if you put $22.5 \times 5 / 1.8$ into a calculator you'll get an exact answer.

Try using the $25/9 \ s$ or $5/1.8 \ s$ to calculate where the truck is when the car stops accelerating. Is that better than using $2.78s$?

yes, they have been taught but i had completely forgotten about it, it's been a while since I've been around with math this much :)

 

[PeroK]

if the truck went 50m in 2.78s and the car went 62.55m it must be still behind the truck

So, what's the next part of the problem?

And it should be exactly $62.5m$!

 

[haruspex]

if the truck went 50m in 2.78s and the car went 62.55m it must be still behind the truck

Right, but how far behind? And given their relative velocities, how long will it take for car to get abreast of the truck?

 

[rssvn]

So, what's the next part of the problem?

And it should be exactly $62.5m$!

Right, but how far behind? And given their relative velocities, how long will it take for car to get abreast of the truck?

it's 37.5m behind the truck, but I am sorry to say that i need another tip, i don't understand how can i figure out the exact time when the car is abreast the truck.

 

[PeroK]

it's 37.5m behind the truck, but I am sorry to say that i need another tip, i don't understand how can i figure out the exact time when the car is abreast the truck.

There are three ways to do it:

1) Intuitively.
2) Using equations of motion
3) By trial and error

For 3) it's like playing a computer game. You move forward 1 second at a time and note the position of the truck and the car and eventually the car must catch the truck.

The point of 3) is that it might give you some idea of which equations are involved. To get you started

t = 0: car = 0m, truck = 37.5m
t = 1: car = 25m, truck = 55.5m
...

 

[rssvn]

There are three ways to do it:

1) Intuitively.
2) Using equations of motion
3) By trial and error

For 3) it's like playing a computer game. You move forward 1 second at a time and note the position of the truck and the car and eventually the car must catch the truck.

The point of 3) is that it might give you some idea of which equations are involved. To get you started

t = 0: car = 0m, truck = 37.5m
t = 1: car = 25m, truck = 55.5m
...

ah yes 125m! i tried to calculate it with 3) but for some reason i was thinking it was a good idea to use the 2.78s time scale to find the right answer and not the 1s which is much much simpler. Can you tell me what would the equations be so solve it? :)

 

[PeroK]

ah yes 125m! i tried to calculate it with 3) but for some reason i was thinking it was a good idea to use the 2.78s time scale to find the right answer and not the 1s which is much much simpler. Can you tell me what would the equations be so solve it? :)

What you are doing in that trial and error example is plotting the position of the car as: $$x_{car} = 0 + v_{car}t = (25m/s)t$$ and the position of the truck $$x_{truck} = 37.5m + v_{truck}t = 37.5m + (18m/s) t$$ where $t$ is the time from the end of the car's acceleration phase.

The equation you need to solve is $$x_{car} = x_{truck}$$

 

[rssvn]

What you are doing in that trial and error example is plotting the position of the car as: $$x_{car} = 0 + v_{car}t = (25m/s)t$$ and the position of the truck $$x_{truck} = 37.5m + v_{truck}t = 37.5m + (18m/s) t$$ where $t$ is the time from the end of the car's acceleration phase.

The equation you need to solve is $$x_{car} = x_{truck}$$

I get it now!
And the answers were a) 62.5 and b) 187.5 (125m plus the initial 62.5 that it went during the acceleration)

 

[PeroK]

I get it now!
And the answers were a) 62.5 and b) 187.5 (125m plus the initial 62.5 that it went during the acceleration)

Except, I don't get $125m$ for the second phase. At $t = 5s$ I get: $x_{car} = 125m$ and $x_{truck} = 127.5m$. The car still has a little bit of catching up to do.

 

[rssvn]

Except, I don't get $125m$ for the second phase. At $t = 5s$ I get: $x_{car} = 125m$ and $x_{truck} = 127.5m$. The car still has a little bit of catching up to do.

Ah, youre right, maybe I'm trying to rush the answer and make silly mistakes like that on the way, t = 5.35s seems to be pretty close, i tried it by trial and error. 5.35s and 133.75m

 

[PeroK]

Ah, youre right, maybe I'm trying to rush the answer and make silly mistakes like that on the way, t = 5.35s seems to be pretty close, i tried it by trial and error. 5.35s and 133.75m

Trial and error is okay, but you still need to find the right answer. It's better to use the equation now that you understand what's going on.

 

[rssvn]

Trial and error is okay, but you still need to find the right answer. It's better to use the equation now that you understand what's going on.

What equation should i use if i don't use the trial and error, isn't the equation you gave Xcar = Xtruck basically using trial and error?