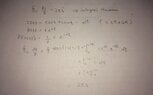- #1
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Cauchy.riemann integral theorem or formula
In summary, the conversation discusses the use of Cauchy's integral theorem and formula in cases where the function is holomorphic inside a circle of radius 1 centered at 2i. It is noted that in the first case where the pole is outside the circle, the function is holomorphic everywhere inside the circle. In the second case, where the pole is inside the circle, Cauchy's integral theorem is used to show that the integral of the function is 0. The use of the Residue Theorem is also mentioned as a way to approach the problem.
Physics news on Phys.org
- #2
Nono713
Gold Member
MHB
- 618
- 4
Note that in the first case the function (which is $\frac{1}{z}$) is holomorphic everywhere inside the circle of radius $1$ centered at $2i$, since it has a single pole at $z = 0$ which is outside this circle. What does that imply?
In the second case, the pole is inside the circle. What does Cauchy's integral theorem say in this case?
In the second case, the pole is inside the circle. What does Cauchy's integral theorem say in this case?
- #3
aruwin
- 208
- 0
Bacterius said:Note that in the first case the function (which is $\frac{1}{z}$) is holomorphic everywhere inside the circle of radius $1$ centered at $2i$, since it has a single pole at $z = 0$ which is outside this circle. What does that imply?
In the second case, the pole is inside the circle. What does Cauchy's integral theorem say in this case?
What does having a pole at z=0 mean? By pole you mean the y-axis?
Last edited:
- #4
Nono713
Gold Member
MHB
- 618
- 4
aruwin said:What does having a pole at z=0 mean? By pole you mean the y-axis?
The function is not holomorphic at z = 0 : there is a "discontinuity" there, but since we're in the complex plane we call these types of discontinuities poles (since it's not really a discontinuity, more of a hole in the domain of the function). See Pole (complex analysis) - Wikipedia, the free encyclopedia
Now if a function is holomorphic everywhere inside a closed convex curve, what does Cauchy's theorem tell you about the integral? (for question 1)
- #5
aruwin
- 208
- 0
Bacterius said:The function is not holomorphic at z = 0 : there is a "discontinuity" there, but since we're in the complex plane we call these types of discontinuities poles (since it's not really a discontinuity, more of a hole in the domain of the function). See Pole (complex analysis) - Wikipedia, the free encyclopedia
Now if a function is holomorphic everywhere inside a closed convex curve, what does Cauchy's theorem tell you about the integral? (for question 1)
That the integral of f(z)=0? Is that right?
- #6
Nono713
Gold Member
MHB
- 618
- 4
aruwin said:That the integral of f(z)=0? Is that right?
That's correct. Cauchy's theorem for convex regions states that if $f$ is a function holomorphic in a convex region $C$ and $\gamma$ is a closed curve in $C$, then:
$$\int_\gamma f(z) ~ \mathrm{d} z = 0$$
Now for the second question note that the function isn't holomorphic inside the circle, because the circle contains zero. So you have to use the more general theorem (the integral theoem). First cite the theorem and see how it applies to your integral.
- #7
aruwin
- 208
- 0
Bacterius said:That's correct. Cauchy's theorem for convex regions states that if $f$ is a function holomorphic in a convex region $C$ and $\gamma$ is a closed curve in $C$, then:
$$\int_\gamma f(z) ~ \mathrm{d} z = 0$$
Now for the second question note that the function isn't holomorphic inside the circle, because the circle contains zero. So you have to use the more general theorem (the integral theoem). First cite the theorem and see how it applies to your integral.
Is this correct for no.2? And by the way, the answer for the first one is just zero, right? But I don't understand that theorem. Why does the integral become zero when f(z) is analytic everywhere within a simply-connected region?
Attachments
- #8
Prove It
Gold Member
MHB
- 1,465
- 24
aruwin said:Is this correct for no.2? And by the way, the answer for the first one is just zero, right? But I don't understand that theorem. Why does the integral become zero when f(z) is analytic everywhere within a simply-connected region?
Proof of Cauchy's Theorem
As for the second, I think what you have done is correct, however I would use the Residue Theorem.
- #9
aruwin
- 208
- 0
Prove It said:Proof of Cauchy's Theorem
As for the second, I think what you have done is correct, however I would use the Residue Theorem.
Read it! Thank you!
FAQ: Cauchy.riemann integral theorem or formula
What is Cauchy-Riemann integral theorem?
The Cauchy-Riemann integral theorem is a fundamental theorem in complex analysis that relates the integral of a function over a closed curve to the values of the function on the interior of the curve. It is named after the mathematicians Augustin-Louis Cauchy and Bernhard Riemann.
What is the Cauchy-Riemann integral formula?
The Cauchy-Riemann integral formula states that for a complex-valued function f(z) defined on a region D in the complex plane, the integral of f(z) over a closed curve C in D is equal to the sum of the values of f(z) at the points inside C, multiplied by a factor of 2πi.
What is the significance of the Cauchy-Riemann integral theorem in complex analysis?
The Cauchy-Riemann integral theorem is significant because it allows us to calculate the integral of a complex function over a closed curve without having to explicitly evaluate the function at every point on the curve. This is especially useful in solving problems involving complex variables and functions.
What are the conditions for the Cauchy-Riemann integral theorem to hold?
The Cauchy-Riemann integral theorem holds if the function f(z) is continuous on the region D, differentiable on the interior of C, and satisfies the Cauchy-Riemann equations on the interior of C. These equations relate the partial derivatives of f with respect to x and y to the partial derivatives of its real and imaginary parts.
How is the Cauchy-Riemann integral theorem used in practice?
The Cauchy-Riemann integral theorem is used in various areas of mathematics and physics, including complex analysis, differential equations, and fluid dynamics. It is also applied in engineering and in the calculation of complex integrals in quantum mechanics. In practical terms, it allows us to simplify and solve complex integrals by leveraging the properties of holomorphic functions.
Similar threads
- Replies
- 8
- Views
- 2K
- Replies
- 2
- Views
- 2K
- Replies
- 2
- Views
- 1K
- Replies
- 1
- Views
- 351
- Replies
- 13
- Views
- 1K
- Replies
- 6
- Views
- 2K
- Replies
- 2
- Views
- 1K
- Replies
- 4
- Views
- 3K
- Replies
- 5
- Views
- 2K
- Replies
- 2
- Views
- 2K
Share: