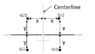Charge Distribution on Metal Sheet

[Saitama]

Homework Statement

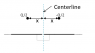
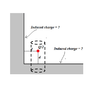
There are two big, same size, uncharged metal sheets in the same plane, lying parallel and very close to each other. The sheets are connected through a piece of wire, and then a pointlike charge Q is placed next to them as shown in the figure. What will the amount of charge on each metal sheet be?

Homework Equations

The Attempt at a Solution

I am not sure but is this related to method of images? But I doubt so because the metal sheet is not grounded. How to proceed then?

Any help is appreciated. Thanks!

 

[BvU]

The wire equates the potential of the plates. At infinity it is 0, so so they could as well be welded together (and grounded, I guess). I think all they want from you is to integrate the induced charge in each of the two halves of the plane.

 

[Saitama]

Hi BvU! :)

The wire equates the potential of the plates. At infinity it is 0, so so they could as well be welded together (and grounded, I guess). I think all they want from you is to integrate the induced charge in each of the two halves of the plane.

Integration? Don't we simply place an image charge in method of images on the other side of conductor?

 

[BvU]

The image charge helps to find the field. So yes, that's good. You are being asked to find the charge distribution on the plates. Or rather: the integral thereof over each half-plane. Nudge nudge...

 

[Saitama]

The image charge helps to find the field. So yes, that's good. You are being asked to find the charge distribution on the plates. Or rather: the integral thereof over each half-plane. Nudge nudge...

I am not sure if I understand that. Please see the attachment. Did I place the image charge correctly? If I find the the field at point P, I can find the "local" charge density at P but how do I set up the integral?

 

[Chestermiller]

Suppose you had two identical charges of magnitude Q/2 placed symmetrically with respect to the centerline. What would the charges on the two plates be? Suppose you had two charges of magnitude -Q/2 and +Q/2 placed symmetrically. What would the charges on the two plates be?

Chet

 

[Saitama]

Hi Chestermiller! :)

Suppose you had two identical charges of magnitude Q/2 placed symmetrically with respect to the centerline.

I have indicated the centerline, do you mean that?

Suppose you had two charges of magnitude -Q/2 and +Q/2 placed symmetrically. What would the charges on the two plates be?

Do I have to place an image charge for -Q/2 and Q/2?

 

[Chestermiller]

Hi Chestermiller! :)I have indicated the centerline, do you mean that?

yes.

Do I have to place an image charge for -Q/2 and Q/2?

The figure has them reversed from the way I intended.

chet

 

[Saitama]

Sorry for the delay in reply.

The figure has them reversed from the way I intended.

chet

I have fixed the sketch but I still don't know how to proceed with the problem. Do I place the image charges as shown in the sketch?

 

[Chestermiller]

Sorry for the delay in reply.


I have fixed the sketch but I still don't know how to proceed with the problem. Do I place the image charges as shown in the sketch?

No. Get rid of the ones below the plate. Just leave the ones above the plate. Now, in order to maintain charge neutrality relative to the centerline, what does the charge have to be on each of the plates (with a charge of -Q/2 above the left plate, and a charge of +Q/2 above the right plate)?

Chet

 

[Saitama]

Now, in order to maintain charge neutrality relative to the centerline, what does the charge have to be on each of the plates (with a charge of -Q/2 above the left plate, and a charge of +Q/2 above the right plate)?

I am honestly lost here, isn't that specifically what the question asks?

The sum of charges on the two plates should be zero so each plate must have equal magnitude of charge but how do I find this magnitude?

 

[Chestermiller]

If both charges were + Q/2, then, by symmetry, you would have no charge on either plate. If the left charge was -Q/2 and the right charge was +Q/2, then, by symmetry, charge would migrate through the wire until you had +Q/2 on the left plate and -Q/2 on the right plate. So by superposition, if you have a charge of +Q above the right plate and no charge above the left plate, the charges on the plates will be +Q/2 on the left plate and -Q/2 on the right plate.

Chet

 

[Saitama]

If both charges were + Q/2, then, by symmetry, you would have no charge on either plate.

Sorry if I am acting stupid but I can't understand why no charge appears on any plate for this case.

... So by superposition, if you have a charge of +Q above the right plate and no charge above the left plate, the charges on the plates will be +Q/2 on the left plate and -Q/2 on the right plate.

But the answer is +Q/4 on right and -Q/4 on left. :(

 

[Chestermiller]

Sorry if I am acting stupid but I can't understand why no charge appears on any plate for this case.

The two plates are connected by a wire, so the sum of the charges on them has to be zero. In the case of +Q/2 and +Q/2, you have to ask yourself how you can have a charge on either of the plates if they have to sum to zero. Which side would be positive and which side would be negative?

But the answer is +Q/4 on right and -Q/4 on left. :(

I must admit, I don't understand how this can be. I'm going to pose this to some friends, and see if they can help.

Chet

 

[Alpharup]

can you try with Gauss Law and flux consideration ?

 

[Saitama]

The two plates are connected by a wire, so the sum of the charges on them has to be zero. In the case of +Q/2 and +Q/2, you have to ask yourself how you can have a charge on either of the plates if they have to sum to zero. Which side would be positive and which side would be negative?

The following is what I think: Consider the left charge +Q/2, it tries to induce a negative charge on left plate and the right charge +Q/2 also tries to induce a negative charge on right plate but the sum must be zero and two negative values never add to zero so the only possibility is that no charge is induced, is this a correct way to think about it?

I must admit, I don't understand how this can be. I'm going to pose this to some friends, and see if they can help.

Ah, please take you time.

 

[Saitama]

Hi sharan swarup! :)

can you try with Gauss Law and flux consideration ?

I am not sure, can you please explain some more?

 

[Alpharup]

since the plate is big, we can uniform charge distribution when the placed. Conceptually speaking , equal and opposite charges are induced on the plates since they are connected. let the change induced on right plate be q. Consider an area perpendicular to both the plates including the charge. Now apply Gauss Law

 

[Chestermiller]

The following is what I think: Consider the left charge +Q/2, it tries to induce a negative charge on left plate and the right charge +Q/2 also tries to induce a negative charge on right plate but the sum must be zero and two negative values never add to zero so the only possibility is that no charge is induced, is this a correct way to think about it?

Yes.

 

[TSny]

Chestermiller's approach is very insightful and I think will lead to the right answer with a little more effort.

With the equal and opposite charges +Q/2 and -Q/2, each plate will become oppositely charged. But only if the two charges $\pm$Q/2 are very far from the center line will the charges on the plates be $\mp$ Q/2.

With the charges +Q/2 and -Q/2 in place, suppose you consider an imaginary plane that lies perpendicular to the plates and contains the line separating the plates. What can you say about the potential at points on this plane?

 

[Saitama]

Hi TSny!

With the charges +Q/2 and -Q/2 in place, suppose you consider an imaginary plane that lies perpendicular to the plates and contains the line separating the plates. What can you say about the potential at points on this plane?

The potential is zero at every point on this plane.

 

[TSny]

Yes, it would be an equipotential surface. Now imagine this imaginary vertical plane replaced by a conducting plate. Would that affect the charge induced on the original horizontal plates?

 

[Saitama]

Yes, it would be an equipotential surface. Now imagine this imaginary vertical plane replaced by a conducting plate. Would that affect the charge induced on the original horizontal plates?

I don't know.

If I place a conducting plate on the centreline, some charge is induced on it but I can't see why it should or should not affect the charge distribution on the horizontal plates.

 

[TSny]

Think about a few simpler cases. Consider an equipotential surface between two infinite parallel plates of opposite charge. If you replaced that surface with a thin conducting sheet, would it affect the electric field outside the sheet or affect the charge distribution on the original plates? Note, though, that there would be surface charge induced on the sheet.

Suppose you had a charged conducting sphere. The equipotential surfaces outside the sphere would be spherical surfaces. If you replaced one of these equipotential surfaces with a thin conducting spherical shell, would it affect the electric field (outside the shell material) or affect the charge distribution on the original conducting sphere? Again, there would be surface charge induced on the inner and outer surfaces of the shell.

In general, if you have found an equipotential surface for an electrostatics problem, then you could replace that surface with a thin conductor and not affect the fields or charge distributions in the system. But, generally, there would be surface charge induced on the surfaces of the thin conductor.

 

[Saitama]

Think about a few simpler cases. Consider an equipotential surface between two infinite parallel plates of opposite charge. If you replaced that surface with a thin conducting sheet, would it affect the electric field outside the sheet or affect the charge distribution on the original plates? Note, though, that there would be surface charge induced on the sheet.

Suppose you had a charged conducting sphere. The equipotential surfaces outside the sphere would be spherical surfaces. If you replaced one of these equipotential surfaces with a thin conducting spherical shell, would it affect the electric field (outside the shell material) or affect the charge distribution on the original conducting sphere? Again, there would be surface charge induced on the inner and outer surfaces of the shell.

No, in both the cases. So in the given case too, the charge distribution is not affected, right? But how does placing a thin conducting surface helps in this case?

 

[TSny]

Right. If you replace the equipotential surface by a conducting plate, then the charges on the original plates do not need to undergo any change in order to satisfy boundary conditions.

See if you can relate the diagrams shown.

 

[Saitama]

Right. If you replace the equipotential surface by a conducting plate, then the charges on the original plates do not need to undergo any change in order to satisfy boundary conditions.

See if you can relate the diagrams shown.

So I guess I have to use method of images now?

But why did we replace the original charge +Q with +Q/2 or are you going to come at this later?

 

[TSny]

So I guess I have to use method of images now?

But why did we replace the original charge +Q with +Q/2 or are you going to come at this later?

I don't think you need images now. Think Gauss' law.

We chose Q/2 to follow Chestermiller's superposition of the {+Q/2, +Q/2} scenario with the {-Q/2, +Q/2} scenario.

 

[Saitama]

I don't think you need images now. Think Gauss' law.

Do I select a cylinder as the gaussian surface?

 

[tiny-tim]

think biiiiiiig

 

[Saitama]

Hi tiny-tim!

think biiiiiiig

Do I have to select a bigger cylinder or my choice of gaussian surface is not correct?

 

[tiny-tim]

this whole problem is about symmetry

there's nothing symmetric about a cylinder in this context

 

[Saitama]

this whole problem is about symmetry

there's nothing symmetric about a cylinder in this context

Would a sphere or cube work?

I would like to know one thing, is this is an advanced (not sure how to define "advanced") problem or is it basic physics I am messing up with?

 

[tiny-tim]

Would a sphere or cube work?

no, i meant taking advantage of one of the basic symmetries of the whole set-up

(and remember, when you have a conductor, part of your gaussian surface is likely to be along the middle of it)

you might get a clue by working backwards from the answer … what do you need the charges to be?

I would like to know one thing, is this is an advanced (not sure how to define "advanced") problem or is it basic physics I am messing up with?

i would classify this as basic trickery

 

[Chestermiller]

It's also possible to "brute force" the solution if you know the equation for the surface charge distribution induced on an infinite flat sheet by a point charge q located at a distance h from the sheet. This would involve doing some integration. This method gives the Q/4 given results you alluded to earlier (PA), but, with the opposite signs.

So far, I for one have not been able to figure out AT's and Tiny Tim's trick method. I'm sure we are missing something very simple, but it just evades me.

Chet