Charlene's question at Yahoo Answers regarding related rates

[MarkFL]

Here is the question:

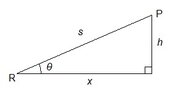
Rate of change of theta?

An airplane is flying at a constant altitude of 8 miles over a radar at a rate of 450mph. At what rate is the angle theta changing when s=25?

I have posted a link there to this topic so the OP can see my work.

 

[MarkFL]

Hello Charlene,

I would first draw a diagram to represent the problem. I will assume the quantity $s$ represents the distance from the radar station directly to the plane. $R$ represents the location of the radar station, and $P$ the location of the plane. I have let $h$ represent the constant altitude of the plane. All linear measures are in miles.

View attachment 970

Since we are given:

(1) \(\displaystyle \left|\frac{dx}{dt} \right|=v\,\therefore\,\frac{dx}{dt}=\pm v\)

where $v$ is the speed of the plane, and we know $h$, we want to relate $\theta$, $x$ and $h$. We may do so by using the definition of the tangent function as follows:

\(\displaystyle \tan(\theta)=\frac{h}{x}\)

Now, implicitly differentiating with respect to time $t$, we obtain:

\(\displaystyle \sec^2(\theta)\frac{d\theta}{dt}=-\frac{h}{x^2}\cdot\frac{dx}{dt}\)

Multiplying through by \(\displaystyle \cos^2(\theta)\) and using (1) we have:

\(\displaystyle \frac{d\theta}{dt}=\pm\frac{hv\cos^2(\theta)}{x^2}\)

Now, from our diagram, we see that:

\(\displaystyle \cos(\theta)=\frac{x}{s}\)

and so we find:

\(\displaystyle \frac{d\theta}{dt}=\pm\frac{hv\left(\frac{x}{s} \right)^2}{x^2}=\pm\frac{hv}{s^2}\)

As we are only asked for the magnitude of the rate of change in $\theta$ with respect to time, we may write:

\(\displaystyle \left|\frac{d\theta}{dt} \right|=\frac{hv}{s^2}\)

Now, using the given data:

\(\displaystyle h=8,\,v=450,\,s=25\)

we find, in radians per hour:

\(\displaystyle \left|\frac{d\theta}{dt} \right|=\frac{8\cdot450}{25^2}=\frac{144}{25}\)