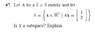- #1
Clandry
- 74
- 0
Hi. I'm trying to check if my approach is right.
The problem is attached.
I need to check these:
1) 0 vector is in S
2) if U and V are in S then U+V is in S
3) if V is in S, then cV where c is a scalar is in S
The 1st condition is not satisfied right?
Since A*[0 0]^t=[0 0]^t≠[1 2]^t?
The problem is attached.
I need to check these:
1) 0 vector is in S
2) if U and V are in S then U+V is in S
3) if V is in S, then cV where c is a scalar is in S
The 1st condition is not satisfied right?
Since A*[0 0]^t=[0 0]^t≠[1 2]^t?