Circular argument? Justification of equipotential points

[tellmesomething]

Homework Statement

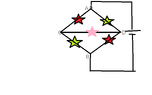
Six resistors are arranged along the edges of a pyramid as shown in figure below. The values of resistances are mentioned with resistances in the figure. Find the effective resistance between A and B.

Relevant Equations

None

I read the solution which stated that ADB and ACB branch are symmetrical. Therefore D and C are equipotential. However this feels like a circular argument when im saying that the branches ADB and ACB are symmetrical, im imagining this circuit without the DC branch. And then im using my previous justification of D and C being equipotential on the new circuit where DC exists. This is sort of like superposition principle? But its too vague like this. Any idea how i can concretely prove this?

 

[haruspex]

when im saying that the branches ADB and ACB are symmetrical, im imagining this circuit without the DC branch.

Why? It is symmetrical with the DC branch.
That said, a rigorous use of the symmetry argument is a bit tricky. Symmetry only says that if there is a solution in which the voltages at C and D are X and Y respectively then there is also one in which they are Y and X respectively.
Can you see how to show X=Y?

 

[tellmesomething]

Why? It is symmetrical with the DC branch.
That said, a rigorous use of the symmetry argument is a bit tricky. Symmetry only says that if there is a solution in which the voltages at C and D are X and Y respectively then there is also one in which they are Y and X respectively.
Can you see how to show X=Y?

Sorry about the very late reply. By this statement "Symmetry only says that if there is a solution in which the voltages at C and D are X and Y respectively then there is also one in which they are Y and X respectively." when would we get this other solution where we get Y as voltage at C and X as voltage at D? I cannot see these symmetries which we initially have to guess to proceed with applying KCL or KVL..and ultimately solve the question. I cannot visualise the two branches being symmetrical, i think i dont know what symmetry means, ive just been told that the resistances of the two branches (ADB and ACB) should be equal for them to be symmetrical but these branches are branching at D and C and i dont find it convincing to leave that out in this argument. Your above quoted statement is interesting and might help me understand what symmetry means if you can elaborate.

EDIT: Directly applying KVL and KCL also gives us correct answers but it would involve many simultaneous equation solving and its probably the least smart way to do it.

 

[tellmesomething]

Why? It is symmetrical with the DC branch.
That said, a rigorous use of the symmetry argument is a bit tricky. Symmetry only says that if there is a solution in which the voltages at C and D are X and Y respectively then there is also one in which they are Y and X respectively.
Can you see how to show X=Y?

X becomes Y and viceversa if the terminals of the battery are interchanged? is that it?

 

[haruspex]

X becomes Y and viceversa if the terminals of the battery are interchanged? is that it?

Yes.

 

[tellmesomething]

Yes.

Ok. What am i doing wrong in the argument of this circuit then?

The stars represent resistances of the same magnitude . Here i want to find eq. resistance between A and B, If the arrangement of the terminals is as shown in the picture and let us assume that absolute potential at C becomes x and absoute potential at D becomes y. If we interchange the terminals, i get no additional info except 2(voltage between BC)=Voltage between AB=2(Voltage between BD); V(ac)=V(ad)
is this appropriate enough to show that there is a solution where absolute potential at D is x and C is y.. since voltage between the same startinhg points are equal

 

[tellmesomething]

I know im not applying it correctly for in a situation like this, i can say that when the terminals are as in my picture potential at C and D are x and y respectively, But i we reverse the terminals, i Would get a solution where D is x and C is y. implying C and D are equipotential points . However that is not correct because theres a current flowing through CD. Can you explain where im going wrong?

 

[haruspex]

Ok. What am i doing wrong in the argument of this circuit then?

View attachment 351510
The stars represent resistances of the same magnitude . Here i want to find eq. resistance between A and B, If the arrangement of the terminals is as shown in the picture and let us assume that absolute potential at C becomes x and absoute potential at D becomes y. If we interchange the terminals, i get no additional info except 2(voltage between BC)=Voltage between AB=2(Voltage between BD); V(ac)=V(ad)
is this appropriate enough to show that there is a solution where absolute potential at D is x and C is y.. since voltage between the same startinhg points are equal

Yes. The symmetry is that if you swap the voltages (by flipping the battery) and then flip the entire diagram about a horizontal axis then the picture (apart from the labels) is identical to what you started with.

View attachment 351512
I know im not applying it correctly for in a situation like this, i can say that when the terminals are as in my picture potential at C and D are x and y respectively, But i we reverse the terminals, i Would get a solution where D is x and C is y. implying C and D are equipotential points . However that is not correct because theres a current flowing through CD. Can you explain where im going wrong?

In this case, flipping the battery and then the entire diagram does not get back to the original diagram. You would also have to flip the ABCD part around the AB axis.

 

[tellmesomething]

Yes. The symmetry is that if you swap the voltages (by flipping the battery) and then flip the entire diagram about a horizontal axis then the picture (apart from the labels) is identical to what you started with.

In this case, flipping the battery and then the entire diagram does not get back to the original diagram. You would also have to flip the ABCD part around the AB axis.

View attachment Equivalent-resistance-between-two-vertices-along-the-body-diagonal-Curio-Physics-1.webp
I am trying to think of a way to find equipotential points here which might help me in simplifying the circuiyt, the terminals are connected between edges A and B. View attachment Equivalent-resistance-between-two-vertices-along-the-body-diagonal-Curio-Physics-1.webp

 

[haruspex]

View attachment 351516
I am trying to think of a way to find equipotential points here which might help me in simplifying the circuiyt, the terminals are connected between edges A and B. View attachment 351525

You mean at nodes A and B?
There is a plane of symmetry, i.e. the circuit on one side of that plane is a mirror image of the other half. Can you spot it?
This means certain pairs of nodes are at the same voltage, so can be collapsed into a single node without affecting any currents. Which pairs?

But the diagram implies the terminals are connected at A and G. If so, the symmetry is of a different kind. Can you see what manipulations of the whole structure effectively leave it unchanged?

 

[tellmesomething]

You mean at nodes A and B?
There is a plane of symmetry, i.e. the circuit on one side of that plane is a mirror image of the other half. Can you spot it?
This means certain pairs of nodes are at the same voltage, so can be collapsed into a single node without affecting any currents. Which pairs?

But the diagram implies the terminals are connected at A and G. If so, the symmetry is of a different kind. Can you see what manipulations of the whole structure effectively leave it unchanged?

There were two parts to this question. First part was to find equivalent resistance between A and G. I got that, by getting D E B as equipoential points and F H C as another pair of equipotential points , reasoning i used is if we were to rotate the cube by 120 degrees about the AG axis we get these points as indistinguishable implying they have the same voltage? then i was able to reduce the diagram to a simple series parallel circuit. The second qsn says to take out equivalent resistance between nodes A and B...


The plane im thinking of for this question cuts two resistances is that valid?

 

[haruspex]

There were two parts to this question. First part was to find equivalent resistance between A and G. I got that, by getting D E B as equipoential points and F H C as another pair of equipotential points , reasoning i used is if we were to rotate the cube by 120 degrees about the AG axis we get these points as indistinguishable implying they have the same voltage? then i was able to reduce the diagram to a simple series parallel circuit.

Good.

The second qsn says to take out equivalent resistance between nodes A and B...


The plane im thinking of for this question cuts two resistances is that valid?

Yes, this is just for finding a symmetry. What we do with it is another matter.

 

[tellmesomething]

Good.

Yes, this is just for finding a symmetry. What we do with it is another matter.

I am not sure if i found the correct plane but i get this after some thinking this might be the plane for reflection ?

 

[tellmesomething]

Good.

Yes, this is just for finding a symmetry. What we do with it is another matter.

About this plane i get E and D; F And C as equipotential points? for H and G i would have to take another plane?

 

[haruspex]

About this plane i get E and D; F And C as equipotential points?

Yes. Can you see that this means you can collapse E and D, likewise F and C, into a single point?

for H and G i would have to take another plane?

There is no other plane of symmetry here.

 

[tellmesomething]

Yes. Can you see that this means you can collapse E and D, likewise F and C, into a single point?

There is no other plane of symmetry here.

Yes but i do not get the answer. This is how the circuit looks after collapsing

For the Decf branch the net resistance we get is R/2+R/2+R=2R
1/(1/2R+2/R)=2R/5
Total resistance = 2R/5+2R=12R/5

The answer is 7R/12

 

[tellmesomething]

Yes. Can you see that this means you can collapse E and D, likewise F and C, into a single point?

There is no other plane of symmetry here.

Sorry i got carried away it is 7R/12 indeed. I added the resistance in series instead of parallel. Thankyou so much