Collision time interval of a gas molecule with wall of container

[vcsharp2003]

TL;DR Summary

Why is the time interval of collision equal to time taken between successive collisions with the wall?

I have been trying to make sense of the derivation of pressure under Kinetic Theory of Gases chapter, but it's not making sense to me when the impulse momentum equation is used for the collision between a gas molecule and the wall of the container.

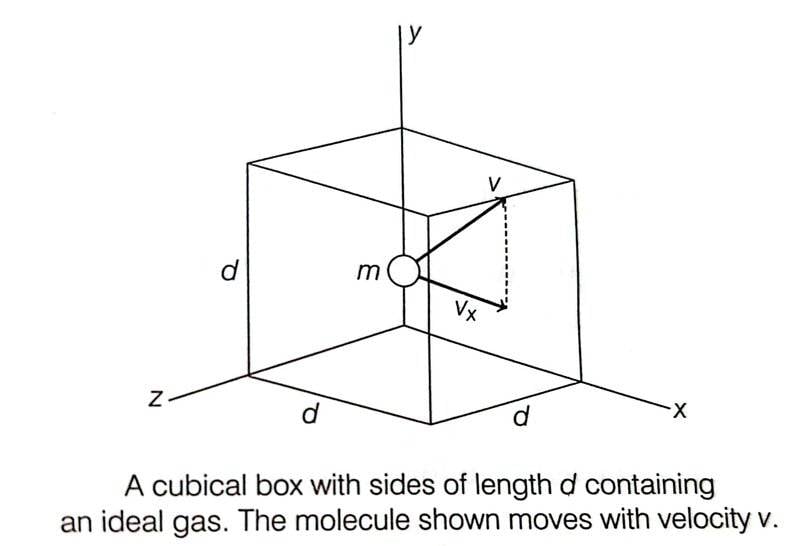
The book says that for the elastic collision between a gas molecule and the wall, $\Delta p_x = -mv_x- mv_x=-2mv_x$ where $\Delta p_x$ is the change in momentum of the gas molecule after colliding elastically with the wall. This makes sense, but the next step seems incorrect to me.

The book says that $\Delta t = \dfrac {2d}{v_x}$ for the equation $F \Delta t = \Delta p_x$. This seem confusing since the $\Delta t = \dfrac {2d}{v_x}$ is the time for the gas molecule to travel to the opposite wall and back to the original wall i.e. time between two successive collisions with the same wall. According to my knowledge, $\Delta t$ should be the time interval of the collision between gas molecule and the wall ( i.e. time interval of contact during collision).

Could someone please explain why we're not taking the time interval of collision but the time between collisions for $\Delta t$?

 

[jbriggs444]

According to my knowledge, $\Delta t$ should be the time interval of the collision between gas molecule and the wall ( i.e. time interval of contact during collision).

Could someone please explain why we're not taking the time interval of collision but the time between collisions for $\Delta t$?

What are we trying to calculate?

If we were trying to calculate the average force of the molecule on the wall during each collision then we would take $\Delta t$ as the duration of a representative collision.

If we are trying to calculate the average force of the molecule on the wall over an extended period of time then we take $\Delta t$ as the average force over a representative cycle.

The text book is trying to motivate the idea of "pressure" in a fluid by modelling the fluid as a bunch of tiny bouncing balls. For this purpose, they do not care about how rapidly momentum is being transferred between fluid and wall over some tiny collision interval during which the force is much higher than average. They want to calculate how much momentum is transferred during a representative time interval.

 

[vcsharp2003]

If we are trying to calculate the average force of the molecule on the wall over an extended period of time then we take Δt as the average force over a representative cycle.

For the extended period of time, we must fix an initial instant and a final instant in order to determine initial and final momentum. If initial instant is just before first collision and final instant is when the molecule is about to collide a second time with the original wall, then $\Delta p_x = -mv_x - (-mv_x) = 0$.

 

[jbriggs444]

For the extended period of time, we must fix an initial instant and a final instant in order to determine initial and final momentum. If initial instant is just before first collision and final instant is when the molecule is about to collide a second time with the original wall, then $\Delta p_x = -mv_x - (-mv_x) = 0$.

Again, focus on what you are trying to calculate.

You want to know about how much momentum has been transferred from molecule to wall during this time interval. During this time interval there has been one interaction. In that interaction an impulse equal to $2mv_x$ was transferred.

There was also an interaction with the back wall where $-2mv_x$ was transferred. But that is not the interface we are looking at.

 

[vcsharp2003]

Again, focus on what you are trying to calculate.

You want to know about how much momentum has been transferred from molecule to wall during this time interval. During this time interval there has been one interaction. In that interaction an impulse equal to $2mv_x$ was transferred.

Ok, that makes sense if we make the wall as our focus for change in momentum, rather than the gas molecule.

 

[jbriggs444]

Ok, that makes sense if we make the wall as our focus for change in momentum, rather than the gas molecule.

The two will be equal and opposite, of course. That's Newton's third law. Or, equivalently, conservation of momentum.

In my mind's eye, we are focusing on the interface and ignoring what happens elsewhere.

 

[vcsharp2003]

The two will be equal and opposite, of course. That's Newton's third law. Or, equivalently, conservation of momentum.

In my mind's eye, we are focusing on the interface and ignoring what happens elsewhere.

It seems that we could simply use the following logic:

momentum change per collision X number of collisions per second = momentum change per second for the gas molecule that is constantly hitting the wall

Then we can say that the momentum change per second is the force exerted on the gas molecule according to Newton's Second Law of Motion.

We can easily see that number of collisions per second for gas molecule with the wall is $\dfrac {v_x}{2d}$.

It seems simpler to follow rather than the original argument.