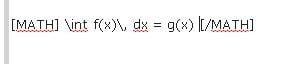- #1
filiphenrique
- 4
- 0
Hey!
How do I integrate ∫tln√(t+1) and ∫4te^(2-0,3t)?
Thanks in advance.
How do I integrate ∫tln√(t+1) and ∫4te^(2-0,3t)?
Thanks in advance.