Complex Numbers - from Polar to Algebraic

[Yankel]

Hello all,

I am trying to find the algebraic representation of the following numbers:

\[rcis(90^{\circ}+\theta )\]

and

\[rcis(90^{\circ}-\theta )\]

The answers in the book are:

\[-y+ix\]

and

\[y+ix\]

respectively.

I don't get it...

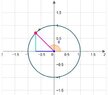
In the first case, if I take 90 degrees (working with degrees, not radians in this question) plus the angel, I get a point in the second quadrant. Why isn't the answer -x+iy ?

View attachment 6854

Thank you !

 

[skeeter]

$$z = r[\cos(90^\circ + \theta) + i\sin(90^\circ + \theta)]$$

$z = r\bigg[\cos(90^\circ)\cos(\theta) - \sin(90^\circ)\sin(\theta) + i[\sin(90^\circ)\cos(\theta) + \cos(90^\circ)\sin(\theta)] \bigg]$

$z = r\bigg[-\sin(\theta) + i \cos(\theta) \bigg]$

$z = -r\sin(\theta) + i\cdot r\cos(\theta) = -y + ix$

---------------------------------------------------------------------------------

$$z = r[\cos(90^\circ - \theta) + i\sin(90^\circ - \theta)]$$

$z = r\bigg[\cos(90^\circ)\cos(\theta) + \sin(90^\circ)\sin(\theta) + i[\sin(90^\circ)\cos(\theta) - \cos(90^\circ)\sin(\theta)] \bigg]$

$z = r\bigg[\sin(\theta) + i \cos(\theta) \bigg]$

$z = r\sin(\theta) + i\cdot r\cos(\theta) = y + ix$

 

[HallsofIvy]

Or just recall that [math]cos(90- x)= sin(x)[/math] and [math]cos(90- x)= sin(x)[/math] from the basic definitions of "sine" and "cosine" instead of using the more general "sum" identity.