Concentric circles are parallel?

[phya]

The straight line parallel to each other is parallel. Concentric circles are parallel,too.

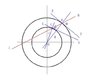
As shown in figure, There is a big circle,Oa，Another one is small, Oc.They are concentric circles. AB is a straight line. AB and Oa are intersections D, AB and Oc are intersections C. EF is a straight line. EF through point D. EF tangent and Oa. GH is a straight line. GH through point C. GH tangent and Oc. R is for Oa radius. r is for Oc radius.

set
β=∠BCH, α=∠BDF, G=CD

is
∠ADO=90-α
∠BCO=90+β

According to the cosine theorem:

G^2=r^2+R^2-2rRcos(180-(90-α+90+β)
After finishing to
G^2=r^2+R^2-2rRcos（α-β） （2）

After finishing (2)
cos（α-β）=（r^2+R^2-G^2）/2rR
If R →∞，r→∞, then
cos（α-β）→1
α→β

When R → ∞， Oa is a straight line， r → ∞，Oc is a straight line，too. This is straight line parallel!Therefore, straight line parallel to the curve of the parallel is special.

After the above discussion, I still have some conclusions are as follows:

Can mutually perpendicular lines, Curve can also mutually vertical.

Flat surface can be parallel, curved surface can also be parallel to each other.

...

 

[HallsofIvy]

What do you mean by 'parallel'? There are some definitions of "parallel" in "concentric circles are parallel" is true and some in which it is not. The "usual" definition of parallel in Euclidean geometry specifically defines only "parallel lines" and so, with that definition, it is not true.

 

[phya]

What do you mean by 'parallel'? There are some definitions of "parallel" in "concentric circles are parallel" is true and some in which it is not. The "usual" definition of parallel in Euclidean geometry specifically defines only "parallel lines" and so, with that definition, it is not true.

Lines divided into curve and linear.All is not straight line.Why can't curve parallel?

 

[Ynaught?]

What do you mean by 'parallel'? There are some definitions of "parallel" in "concentric circles are parallel" is true and some in which it is not. The "usual" definition of parallel in Euclidean geometry specifically defines only "parallel lines" and so, with that definition, it is not true.

I understand the definition of parallel lines to be, when two lines in a plane equidistant part at every point and never intersecting they are parallel. Nothing in that states the lines need to be straight. Which must be the true part you refer to. But I don't see the not true part... Unless maybe that lines of latitude when viewed from the pole appear to be concentric circles but they are not parallel because they do not lie in the same plane?

 

[phya]

I understand the definition of parallel lines to be, when two lines in a plane equidistant part at every point and never intersecting they are parallel. Nothing in that states the lines need to be straight. Which must be the true part you refer to. But I don't see the not true part... Unless maybe that lines of latitude when viewed from the pole appear to be concentric circles but they are not parallel because they do not lie in the same plane?

Three-dimensional space straight line can be parallel.Three-dimensional space curved line can also be parallel.

 

[phya]

Does not intersect was not equal to that is parallel. For example, two curves do not intersect, but actually not necessarily is parallel. Two straight lines do not intersect only then possibly are parallel.

Why said that possibly is parallel? Please read in the appendix the chart. In chart two straight lines not parallel, also does not intersect. These two lines are infinite long, but they do not intersect, they are not also parallel.

 

[Mentallic]

If you have some curve y=f(x) then you can use your own definition to say that another curve y=f(x)+c where c is some non-zero constant is parallel to the other. This is generally not considered the true definition of parallel. Parallel is only used to describe lines and planes, not curves.

How are the two lines in that diagram infinitely long? You can see where they end!

 

[HallsofIvy]

Does not intersect was not equal to that is parallel. For example, two curves do not intersect, but actually not necessarily is parallel. Two straight lines do not intersect only then possibly are parallel.

Why said that possibly is parallel? Please read in the appendix the chart. In chart two straight lines not parallel, also does not intersect. These two lines are infinite long, but they do not intersect, they are not also parallel.

Read in what appendix? Again, please state your definition of "parallel"! These statements are true for some definitions of parallel and not for others. If you do not definie "parallel" people will be forced to assume you mean "parallel" as defined in Euclidean geometry where these statements you make are NOT true.

 

[Mentallic]

Read in what appendix?

He means the diagram at the end of his post.

 

[phya]

If you have some curve y=f(x) then you can use your own definition to say that another curve y=f(x)+c where c is some non-zero constant is parallel to the other. This is generally not considered the true definition of parallel. Parallel is only used to describe lines and planes, not curves.
How are the two lines in that diagram infinitely long? You can see where they end!

The definition is reflects the nature, is to the nature induction and the summary. A parallel definition kind of natural phenomenon. The curve parallel is also one kind of natural phenomenon. Should also contain this kind of phenomenon in humanity's parallel concept. A parallel key character is the distance maintains invariable. Regardless of being the straight line, the curve is so. This is the parallel essence. It is the straight line or the curve, this is unimportant.Humanity's understanding is parallel starts from the straight line, therefore the humanity is limited easily. Therefore the humanity knows the non-European geometry with difficulty.

 

[phya]

The definition is reflects the nature, is to the nature induction and the summary. A parallel definition kind of natural phenomenon. The curve parallel is also one kind of natural phenomenon. Should also contain this kind of phenomenon in humanity's parallel concept. A parallel key character is the distance maintains invariable. Regardless of being the straight line, the curve is so. This is the parallel essence. It is the straight line or the curve, this is unimportant.Humanity's understanding is parallel starts from the straight line, therefore the humanity is limited easily. Therefore the humanity knows the non-European geometry with difficulty.

 

[Mentallic]

Humanity's understanding is parallel starts from the straight line, therefore the humanity is limited easily.

You obviously don't know what the word "define" means, since we've mentioned it to you dozens of times already.

non-European geometry

lol non-Euclidean?

 

[phya]

You obviously don't know what the word "define" means, since we've mentioned it to you dozens of times already.

lol non-Euclidean?

Non-Euclidean Geometry？

 

[phya]

You obviously don't know what the word "define" means, since we've mentioned it to you dozens of times already.
lol non-Euclidean?

We may the narrow definition parallel, is also parallel is only about straight line between being parallel. But it in fact, parallel may also be generalized. Before we think the geometry only then the Euclid geometry, but does not have other geometries, now we knew that also has the non-Euclid geometry. After having discovered non-Euclid geometry, we may say that the Euclid geometry is only the narrow geometry.Not right?

 

[Mentallic]

If you don't know what euclidean geometry is, please explain what you meant by european geometry

In non-euclidean geometries such as spherical and hyperbolic geometries, we use the term "geodesics" rather than straight lines so as not to confuse the two. Since parallel lines can intersect in spherical geometry which disobeys our definition of parallel (it is assumed in these definitions that we are using euclidean geometry anyway).

The definition of parallel is not generally extended to curves, but you can make it that way if you like. This doesn't mean you are going to convince us all that the definition of parallel needs to be extended because you think it does.

 

[phya]

If you don't know what euclidean geometry is, please explain what you meant by european geometry

In non-euclidean geometries such as spherical and hyperbolic geometries, we use the term "geodesics" rather than straight lines so as not to confuse the two. Since parallel lines can intersect in spherical geometry which disobeys our definition of parallel (it is assumed in these definitions that we are using euclidean geometry anyway).

The definition of parallel is not generally extended to curves, but you can make it that way if you like. This doesn't mean you are going to convince us all that the definition of parallel needs to be extended because you think it does.

The slip of the pen is the very normal matter. Has the understanding to the geometry the human, actually does not know the non-Euclid geometry, this possible? But ridicules others because of others' slip of the pen, should not.

 

[HallsofIvy]

No one has ridiculed you. We have, however, repeatedly asked you to define what you mean by "parallel" any you have not done so.

 

[phya]

No one has ridiculed you. We have, however, repeatedly asked you to define what you mean by "parallel" any you have not done so.

Ask when the Euclid geometry how to define parallel?

 

[HallsofIvy]

I assume that English is not your first language. Euclidean geometry does NOT "define parallel". It does define "parallel line" and, as I said before, in Euclidean geometry, parallel only applies to straight lines. So apparently, in your question you are NOT talking about Euclidean geometry. I ask, for the third time, how do you define "parallel" in this question?

 

[phya]

I assume that English is not your first language. Euclidean geometry does NOT "define parallel". It does define "parallel line" and, as I said before, in Euclidean geometry, parallel only applies to straight lines. So apparently, in your question you are NOT talking about Euclidean geometry. I ask, for the third time, how do you define "parallel" in this question?

Indeed, in the Euclid geometry, parallel is between straight line being parallel. I have a question, ask, the line segment is may also be parallel? Sorry, please use is or is not replied.

 

[Mentallic]

Yes a line segment can be parallel to another line or line segment. In the study of geometry you encounter parallel line segments all the time.

 

[phya]

Yes a line segment can be parallel to another line or line segment. In the study of geometry you encounter parallel line segments all the time.

We may regard as the curve are composed of the innumerable strip small line segment, if composes two curves the corresponding line segments is each other parallel, then these two curves are also parallel?

 

[HallsofIvy]

You are now faced with the problem of determining precisely HOW you are going to "regard the curve as composed of innumerable small line segments" (there are many different ways of doing that- and they give different results) as well as telling which line segments are "corresponding". Until you tell us that (and I suspect that both tasks are much harder than you might think), no one can answer your question.

IF you define "parallel curves" by "at any point on one curve, the perpendicular to the curve at that point is also perpendicular to the second line and the distance from one curve to the other curve, measured along that line, is constant (independent of the initial point)", then, yes, concentric circles are "parallel" by that definition. But that is not the only possible definition of "parallel" and certainly is NOT the definition in Euclidean geometry.

In Euclidean geometry, "parallel" is only defined for lines and is simply, "two lines are parallel if and only if they do not intersect". If you drop the "lines" requirement and use that definition, then, yes, concentric circles are "parallel" but then so are any circles that do not intersect, or any line segments that do not intersect, whatever their angular orientation, any curves that do not intersect, etc.

(Parallel line segments is not, strictly speaking, defined in Euclidean geometry but some texts, for specialized purposes, define line segments to be "parallel" if and only if the lines they lie on are parallel.)

 

[Mentallic]

Well of course the tangents at some exact point on each curve are going to be parallel. This doesn't mean the general meaning of parallel is extended to curves as well. Parallel is only used for lines, but if you have a reason to change that meaning for yourself, then by all means do so. This isn't going to change the general understanding of the term parallel though.

 

[phya]

Yes a line segment can be parallel to another line or line segment. In the study of geometry you encounter parallel line segments all the time.

If two regular polygon's corresponding sides are mutually parallel, then these two regular polygons are parallel? If the answer is affirmative, then why the concentric circle is not parallel?

 

[phya]

You are now faced with the problem of determining precisely HOW you are going to "regard the curve as composed of innumerable small line segments" (there are many different ways of doing that- and they give different results) as well as telling which line segments are "corresponding". Until you tell us that (and I suspect that both tasks are much harder than you might think), no one can answer your question.

IF you define "parallel curves" by "at any point on one curve, the perpendicular to the curve at that point is also perpendicular to the second line and the distance from one curve to the other curve, measured along that line, is constant (independent of the initial point)", then, yes, concentric circles are "parallel" by that definition. But that is not the only possible definition of "parallel" and certainly is NOT the definition in Euclidean geometry.

In Euclidean geometry, "parallel" is only defined for lines and is simply, "two lines are parallel if and only if they do not intersect". If you drop the "lines" requirement and use that definition, then, yes, concentric circles are "parallel" but then so are any circles that do not intersect, or any line segments that do not intersect, whatever their angular orientation, any curves that do not intersect, etc.

(Parallel line segments is not, strictly speaking, defined in Euclidean geometry but some texts, for specialized purposes, define line segments to be "parallel" if and only if the lines they lie on are parallel.)

First, does not intersect is not necessarily parallel, we pay attention to 6 buildings the charts: Has two line segments in that circular plane, they do not intersect, also not parallel, we infinite enlarge this circular plane the diameter, in the circle line segment also meet the infinite extension, but they forever will not intersect, but will not be parallel.

 

[phya]

What is the parallel essence? Does not intersect, the distance maintains invariable? In my opinion the parallel essence is the distance maintains invariable, but is not does not intersect.

 

[phya]

In 25 building charts, if these two regular polygon's corresponding sides are parallel, then they are also parallel?

 

[94JZA80]

I understand the definition of parallel lines to be, when two lines in a plane equidistant part at every point and never intersecting they are parallel. Nothing in that states the lines need to be straight. Which must be the true part you refer to. But I don't see the not true part... Unless maybe that lines of latitude when viewed from the pole appear to be concentric circles but they are not parallel because they do not lie in the same plane?

i agree with your first statement that lines (or surfaces) don't need to be straight (or flat) in order to be parallel.

but your second statement is false. if you're standing at either of the Earth's poles and looking down at your feet, not only do lines of latitude appear to be concentric circles, but they also appear parallel. now i don't know if, by definition, concentric circles must lie in the same plane. but i would imagine that while some folks would argue that the circles are concentric b/c they share a common center, others might argue that they only "appear" concentric b/c they do not actually share a common center (b/c they don't all lie in the same plane) - rather their respective centers are all aligned with the axis that runs through the Earth's poles. so again, i don't know if lines of latitude are considered to be concentric by the strictest definition or not...

...but that's neither here nor there, as I'm trying to show that lines of latitude not only appear parallel, but in fact ARE parallel, despite not lying in the same plane. imagine again that you are at one of the Earth's poles staring at your feet. now imagine a straight line originating from the center of the Earth and intersecting an arbitrary point on the equator. there is exactly one point on each line of latitude that lies directly above this imaginary line that intersects the center of the Earth and the equator. take the 20th and 40th parallels (specific lines of latitude) for instance - connect the two points (one from each line of latitude) that lie directly above your imaginary line that intersects the center of the Earth and some arbitrary point on the equator. measure the distance between those two points lying on different lines of latitude and call it D. now look down at your feet again, and imagine another line intersecting the center of the earth, but this time intersecting a different point on the equator. if you find the points on the 20th and 40th parallels that lie directly above this newly constructed imaginary line, you'll find that the distance measured between them is still D. in fact, this holds for any imaginary line that intersects center of the Earth and any point on the equator. hence, the two lines of latitude at 20° and 40° respectively are equidistant everywhere, and are therefore parallel, despite not lying in the same plane. its also the reason they call them the 20th and 40th "parallels."

i can also see how the OP's argument extends from curved lines to curved surfaces. concentric spheres is a perfect example of parallel surfaces. for instance, take two concentric spheres with different radii (so that they cannot be mistaken for identical spheres). any line that intersects their common center will be orthogonal to both concentric spheres' surfaces, no matter where it intersects them. if we label the distance between those two points of intersection "D", then we find again that any line intersecting the concentric spheres' common center will produce two points (one on each sphere) a distance D apart. in other words, D = r2 - r1 (the difference in the length of one radius and the other) is the same everywhere, no matter where on the surface of each sphere we decide to take our radius measurement from. if the difference in radii is the same everywhere, then the spheres are parallel.

i guess this is just an elaboration on the OP's response to your conjecture, just in case it wasn't immediately clear why lines of latitude are parallel despite not lying in a common plane...of course, as we've seen from the responses of many others, this may all be true according to some definitions, and completely false by others. the definition of "parallel" i suppose has analogs depending on the space you're working in (2 dimensions, 3 dimensions, etc.) and their varying geometries (euclidean, non-euclidean, etc.)...i know some folks would shy away from calling anything other than straight lines in euclidean space "parallel," and would revert to describing such things as "equidistant," "similar," "congruent," etc. but i still feel that the word "parallel" better describes many of these curved lines or surfaces and their orientations with respect to one another than other words from the vocabulary of geometry, even if by definition the word "parallel" only concerns straight lines in euclidean space...

...just my 2 cents

 

[Dr Lots-o'watts]

What is the parallel essence? Does not intersect, the distance maintains invariable? In my opinion the parallel essence is the distance maintains invariable, but is not does not intersect.

The word parallel only applies to straight lines. There is no need to apply it to circles. For circles, you may say that for concentric circles, their tangents at the same angular position are parallel.

If you want a word for describing how certain curves don't intersect, you might want to create a new word. But chances are any 2 such curves you can imagine have already been described exactly already using words such as "correspond", "in phase", "equidistant" etc.