Concentric circles are parallel?

[phya]

The word parallel only applies to straight lines. There is no need to apply it to circles. For circles, you may say that for concentric circles, their tangents at the same angular position are parallel.

If you want a word for describing how certain curves don't intersect, you might want to create a new word. But chances are any 2 such curves you can imagine have already been described exactly already using words such as "correspond", "in phase", "equidistant" etc.

What is the parallel essence?

 

[phya]

The word parallel only applies to straight lines. There is no need to apply it to circles. For circles, you may say that for concentric circles, their tangents at the same angular position are parallel.

If you want a word for describing how certain curves don't intersect, you might want to create a new word. But chances are any 2 such curves you can imagine have already been described exactly already using words such as "correspond", "in phase", "equidistant" etc.

Before we only knew that has the Euclid geometry, that the ‘geometry’ this word specially refers to the Euclid geometry? The non-Euclid geometry may not use the ‘ geometry’ this word?

 

[Dr Lots-o'watts]

It's only a matter of vocabulary. I don't see why you want to use the word "parallel" so much.

Geometry is divided into "Euclidean geometry" and "non-euclidean geometry" for good reason.

You're saying perhaps we can now have "Euclidean parallel", "Euclidean circular parallel", "non-euclidean parallel", etc. I don't have any problem with that, but I don't see any reason why one would spend a lifetime trying to convincing every mathematician to use this new terminology.

 

[CRGreathouse]

It's difficult to extend the definition of parallel to objects other than lines (or subsets of lines containing at least two distinct points, I suppose). It's easy to see that approximating concentric circles as n-gons and taking the limit as n increases without bound (as earlier suggested on this thread) doesn't work, since the sides could be offset such that no segments are parallel to any segment in the other approximating n-gon.

What is the parallel essence? Does not intersect, the distance maintains invariable?

FWIW, the statement "parallel lines are always equidistant" (at perpendiculars) is equivalent to the parallel postulate, that is, forces you (in some sense) into Euclidean geometry.

It's not really clear how to extend the concept of equidistant to other shapes, but I don't see any problem in using it for circles. Two circles are equidistant if and only if they are concentric or both of zero radius.

 

[phya]

It's only a matter of vocabulary. I don't see why you want to use the word "parallel" so much.

Geometry is divided into "Euclidean geometry" and "non-euclidean geometry" for good reason.

You're saying perhaps we can now have "Euclidean parallel", "Euclidean circular parallel", "non-euclidean parallel", etc. I don't have any problem with that, but I don't see any reason why one would spend a lifetime trying to convincing every mathematician to use this new terminology.

We do not need to establish that many special terminology. The parallel concept is unified, is also the distance maintains invariable, regardless of this to curve, to the straight line, is to the surface, to the plane is so.

 

[Phrak]

Ya-all quite pickin' on phya. You all should know better. Good grief!

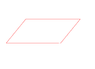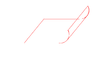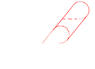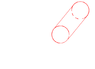
Normally, phya, in the way these things are taught, right or wrong, a vector or a line is independent of the coordinates in which they are described. It's really a matter of convention. In this convention, we assume that a line is independent of the coordinates, such as x,y and z by which we measure its parts. It has an existence of it's own, and the coordinates are a matter of choice.

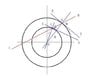
You, on the other hand, are taking the opposite view. You take two parallel lines and wrap them in a circle. You are taking the coordinates as fundamental and the line is a mutable object.

In your system x-->radius and y-->an angle, so that parallel lines in in (x,y) are still parallel. There's nothing wrong with this, it's not the convention so people get confuse, but it certainly not wrong--just different, and a perspective that may have great value.

 

[phya]

“crosses outside the straight line a spot to have two straight lines and the known straight line at least parallel”, I believed that non-Euclid geometry's this view is wrong. Because, first, in the non-Euclid geometry's straight line is not in the Euclid geometry straight line, second, does not intersect was not equal to that is parallel, does not intersect regards is parallel, this has confused parallel and not the parallel concept. If we regard the circle the straight line, then may also say: Crosses outside the straight line a spot to be possible to make the innumerable strip straight line (this passes through known point, but does not intersect with known circle these circles) do not intersect with the known straight line.

 

[CRGreathouse]

“crosses outside the straight line a spot to have two straight lines and the known straight line parallel non-Euclid geometry some views is at least” wrong.

Who are you responding to?

 

[phya]

Who are you responding to?

My this reply not in view of anybody.

 

[CRGreathouse]

My this reply not in view of anybody.

I was just trying to understand the quotation marks (and, for that matter, the quotation).

 

[phya]

I was just trying to understand the quotation marks (and, for that matter, the quotation).

What not clearly do you have?

 

[phya]

Like the chart shows, nearby one rectangular plane's about two is parallel, if we become this rectangle uniplanar bending the proper circle barrel, nearby rectangular about two becomes two curves, ask that by now these two lines no longer were parallel?

 

[phya]

About curve parallel and non-Euclid geometry mistake and absolute geometry completion


First, about concentric circle parallel

May say like this that the straight line parallel is the concentric circle parallel special row, but the concentric circle parallel is the curve parallel special row. Curve parallel is general parallel, but the straight line parallel is quite special being parallel.

Below we have a look at the concentric circle the nature.

As shown in Figure 1, great-circle and small circle concentric, straight line AB and the great-circle have point of intersection C, straight line AB and the small circle have point of intersection D, straight line EF are the great-circle tangents, and D is a tangential point, straight line GH is the small circle tangent, and C is a tangential point, R is the great-circle radius, r is the small circle radius.

Supposition

β=∠BCH, α=∠BDF, β and α is the corresponding angle mutually, β is the great-circle corresponding angle, α is the small circle corresponding angle, G=CD.

Then

90-α=∠ADO
90+β=∠BCO

According to sine law:

R/sin(90+β)=r/sin(90-α)

After the reorganization,

R/cosβ=r/cosα

Reorganizes again

Rcosα=rcosβ （1）

By (1) obviously, when R and r tend infinite, the great-circle is the straight line, the small circle is also a straight line, β=α, this is also straight line being parallel. Therefore the straight line parallel is only the concentric circle parallel extreme.

According to law of cosines:

G^2=r^2+R^2-2rRcos(180-(90-α+90+β)

After the reorganization,

G^2=r^2+R^2-2rRcos（α-β） （2）

After reorganization (2) formula, obtains

cos（α-β）=（r^2+R^2-G^2）/2rR （3）

By (3) obviously, when R and r tend infinite, the great-circle is the straight line, the small circle is also a straight line, β=α (corresponding angle equal), this is also straight line being parallel. Therefore the straight line parallel is only the concentric circle parallel extreme.

We may say, in a plane, so long as G^2=r^2+R^2-2rRcos (α-β), then two circles are parallel (concentric), otherwise is not parallel (not concentric).

After the above discussion, the conclusion which I obtain is:

When straight line the line, the curve is also the line, the line including the straight line and the curve. The line may not by the understanding be a straight line merely.

In the curve, the circle is a straight line. The straight line is that kind of radius infinitely great circle.

The straight line may the mutually perpendicular, the curve also be possible the mutually perpendicular. (i.e., straight line may mutually parallel, curve may also mutually parallel). Is vertical including the straight line between vertical and between curve vertical.

The angle side may be a straight line, may also be the curve, the angle including the linear angle and the curvilinear angle.

In the plane, the curve triangle's angle's summation may be bigger than or be smaller than π.

The surface may also be parallel mutually.The concentric spherical surface is mutually parallel.

The spherical surface is in the space these maintains with the fixed point the parallel distance is the r these spot set.The spherical surface and the center are parallel.

。。。。。。


Second, diagrammatic curve parallel

As shown in Figure 2:

In the plane, the rectangular two red side is parallel,

If we cause the rectangle to turn the cylinder, then that two red side is not parallel? I think them parallel, because between them the distance is constant.

If we cause the circular cylinder to turn the frustum, then that two red side is not parallel? I think them parallel, because between them the distance is constant.

If we cause the frustum to press the plane, then that two red side is not parallel? I think them parallel, because between them the distance is constant. (the attention, that two red side was precisely a concentric circle by now! ).

Therefore, once we acknowledge the straight line to be possible mutually parallel, then we can also not but acknowledge the curve also to be possible mutually parallel! The Euclid geometry only realized straight line parallel, but has neglected curve being parallel. He has received the historical limitation.

What is the parallel essence? This is the distance maintains constant invariable! No matter but whether is the straight line!



Third, about the non-Euclid geometry (including spherical geometry)

The spherical geometry thought that in the spherical surface does not have the parallel line. Actually this view is correct, is also wrong. In the spherical surface does not have the straight parallel line, but in the spherical surface actually has the curving parallel line. For instance, in the spherical surface latitude parallel is mutually parallel. Measures the grounding not mutually parallel, but this was not equal to said that in the spherical surface other curves may not be mutually parallel.

In the plane, through a known straight line's outside spot, has a straight line and the known straight line parallel, this is correct. In the spherical surface, through a known curve's outside spot, has a curve and the known curve parallel, this is also correct. Therefore may not remove the axiom of parallels in the spherical geometry! Certainly may not remove the axiom of parallels in the hyperbolic geometry!

The non-Euclid geometry thought: Crosses a straight line spot to be possible to make two straight lines and the known straight line at least parallel, actually this is the idea has the question. First, this confused has been parallel with the concept which did not intersect, because did not intersect was not equal to that was parallel, (in the Euclid geometry, because was parallel is limited in straight line, but in straight line, did not intersect as if is parallel, but in curve, did not intersect not necessarily is parallel); Second, this has confused the straight line and the curve difference, because the non-Euclid geometry said the straight line is a curve in fact!




Fourth, about absolute geometry

After the above revision, three geometries will unify completely and fuse one to be overall, humanity's geometry henceforth only will then perhaps become the absolute geometry.

 

[phya]

https://www.physicsforums.com/attachment.php?attachmentid=28468&d=1285242201"

 

[HallsofIvy]

I asked you, 42 posts ago, to state what definition of "parallel" you are using. Since you have refused to do so, I don't see how anyone can say anything sensible about your statements.

 

[phya]

I asked you, 42 posts ago, to state what definition of "parallel" you are using. Since you have refused to do so, I don't see how anyone can say anything sensible about your statements.

Parallel is the distance maintains invariable, for example, between the distance maintains invariable, between the curve the distance maintains invariable, between the surface the distance maintains invariable and so on.

 

[G037H3]

Concentric circles are an example of parallel curves.

 

[Mentallic]

You can see concentric circles as being parallel from the perspective of the centre of each circle (the distance from the first to the second circle is constant, as measured from the centre) but from another viewpoint (say, and observer looking towards both circles) then they are suddenly not following this rule.

From the centre of the circles viewpoint, this says in coordinate geometry that x^2+y^2=r^2 is "parallel" to x^2+y^2=R^2

but from the observer which is found situated far along the y-axis (as to observe both circles head on) then he will see two circles as "parallel" if they are of the form
x^2+y^2=r^2 and x^2+(y-c)^2=r^2

Now one property of parallel lines is that if line A is parallel to line B and line A is parallel to line C then B is parallel to C. Following this rule, this would mean that x^2+y^2=R^2 is "parallel" to x^2+(y-c)^2=r^2 ? This is why we give concentric circles a description other than "parallel". And we should keep it that way to avoid ambiguity.

 

[phya]

concentric circles are an example of parallel curves.

yes!

 

[phya]

You can see concentric circles as being parallel from the perspective of the centre of each circle (the distance from the first to the second circle is constant, as measured from the centre) but from another viewpoint (say, and observer looking towards both circles) then they are suddenly not following this rule.

From the centre of the circles viewpoint, this says in coordinate geometry that x^2+y^2=r^2 is "parallel" to x^2+y^2=R^2

but from the observer which is found situated far along the y-axis (as to observe both circles head on) then he will see two circles as "parallel" if they are of the form
x^2+y^2=r^2 and x^2+(y-c)^2=r^2

Now one property of parallel lines is that if line A is parallel to line B and line A is parallel to line C then B is parallel to C. Following this rule, this would mean that x^2+y^2=R^2 is "parallel" to x^2+(y-c)^2=r^2 ? This is why we give concentric circles a description other than "parallel". And we should keep it that way to avoid ambiguity.

Your understanding is not necessarily correct, like the chart shows, the left side two circles are parallel, but the right side two circles are not parallel. Why? Because the circle and the circle distance is dissimilar. The attention, I said am the center of circle and the center of circle distance.

 

[phya]

You can see concentric circles as being parallel from the perspective of the centre of each circle (the distance from the first to the second circle is constant, as measured from the centre) but from another viewpoint (say, and observer looking towards both circles) then they are suddenly not following this rule.

From the centre of the circles viewpoint, this says in coordinate geometry that x^2+y^2=r^2 is "parallel" to x^2+y^2=R^2

but from the observer which is found situated far along the y-axis (as to observe both circles head on) then he will see two circles as "parallel" if they are of the form
x^2+y^2=r^2 and x^2+(y-c)^2=r^2

Now one property of parallel lines is that if line A is parallel to line B and line A is parallel to line C then B is parallel to C. Following this rule, this would mean that x^2+y^2=R^2 is "parallel" to x^2+(y-c)^2=r^2 ? This is why we give concentric circles a description other than "parallel". And we should keep it that way to avoid ambiguity.

In group of concentric circles, if A is parallel to B, B is parallel to C, then A is also parallel to C.

 

[Mentallic]

Your understanding is not necessarily correct

I beg to differ, notice that I wrote

but from the observer which is found situated far along the y-axis (as to observe both circles head on) then he will see two circles as "parallel" if they are of the form
x^2+y^2=r^2 and x^2+(y-c)^2=r^2

Your diagram doesn't express what I mentioned. So I took the liberty of explaining it to you in pretty pictures.

http://img691.imageshack.us/img691/9694/parallel.th.png
This diagram is supposed to be 2 dimensional.
In the first row of examples, the red and orange lines are of equal length. The circles are of the same size.

So when you say curves are parallel, we could be confused into thinking it's two circles above. How can we know you mean concentric circles? If you do mean concentric circles, then just say so. They already have a name for those so there's no need to try and label them as being parallel.
There are inconsistencies in trying to extend the meaning of parallel since it needs to hold for all cases. Clearly, from my diagram, if you consider it parallel to be the observer from a fixed point (as in the case of concentric circles) then why aren't two lines parallel if you observe them in the same way?

And to touch up on another point. When two parallel lines are transposed (moved) they are still parallel to each other. In your diagram, this rule breaks down. You move one of those concentric circles and suddenly they aren't "parallel" to each other anymore.

 

[G037H3]

I'm not sure that last point is exactly fair, because since a line is the same in homogeneous space, and distances between circles depend on their center and radius, it is much easier to claim that circles can't be parallel.

I stand by my previous post, concentric circles are parallel curves, but not parallel lines, because in mathematics lines are generally perfectly straight.

 

[Mentallic]

The point is, using the term "parallel curve" creates an ambiguity as I've already shown, unless it's specifically defined to be one or the other - which it isn't.

What is wrong with sticking to the term "concentric circles" anyway? I could just as easily argue that parallel lines are also concentric lines. It's just silly.

 

[G037H3]

The point is, using the term "parallel curve" creates an ambiguity as I've already shown, unless it's specifically defined to be one or the other - which it isn't.

What is wrong with sticking to the term "concentric circles" anyway? I could just as easily argue that parallel lines are also concentric lines. It's just silly.

I don't disagree, but I feel that the main point of the thread is to assert that concentric circles are parallel, which they are, because they're parallel curves. As long as the OP understands the difference between parallel lines (all the points that the line consists of can be rotated about themselves 360 degrees and the line remains parallel) and parallel curves, I don't really have a problem with the assertion.

 

[Mentallic]

Ok but if concentric circles are parallel, then surely circles of the same size that have been transposed aren't parallel. But with this same property of transposition for curves, phya claims they are parallel too.

 

[G037H3]

I'm sorry, but could you please elaborate on what you mean by transposition? :)

My knowledge in this kind of topic comes from studying Heath's version of Euclid's Elements, btw. I'm only about 10% through it, but it is a very beautiful book.

 

[Mentallic]

Tranpose or to move something. To slide in other words.

 

[G037H3]

Oh, I thought you meant to switch position, which makes no sense, because concentric circles have the same center, so they can't change places.

Circles of the same radius that have been moved aren't parallel in the usual sense, I agree. But if you take the curve of the half-circle on the same side of both circles, obviously they're the same, so they would be parallel curves, no? As in, there is a 1 to 1 match-up between points on the first curve and points on the last curve in that the value of the shortest distance between points that have the same value on the curve relative to the rest of the curve remains the same. Or, simply put, the curves fit perfectly with each other if the distance between the points are reduced to zero.

 

[Mentallic]

Yes, they're concentric circles. One property of concentric circles is that given some line that cuts through the centre of the circles, at the point where it intersects the circumference of each circle, the tangents made at those points will be parallel.

My parallel lines are concentric lines too in that case.