Conditions for spacetime to have flat spatial slices

[PeterDonis]

I've shown that the "obvious" answer (at 1.3 billion light years distance) is that the second observer ages 13.65 billion years, while the Earth ages 13.7 billion years. 13.65 billion and 13.7 billion are very close. This means that any observer within 1.3 billion light years should have approximately the *same* amount of proper time since the Big Bang event.

According to the "naive" calculation in the ECC frame, yes. But the difference will get larger as you go out to larger distances in the ECC frame. In the "cosmological" frame, the frame in which the FRW metric is written, *all* observers at the same cosmological time t have experienced *exactly* the same proper time since the Big Bang. See next comment.

So now I need some clarification on what you've said above. "the second observer's proper time since the Big Bang at event E will be the *same* as the Earth's proper time since the Big Bang at event O" When you say this, are you already taking into account the speed of light delay? For instance, the image of a galaxy 1.3 billion light years away should not look 13.7 billion years old, but should look 12.4 billion years old, because the light originated from an event 1.3 billion years ago.

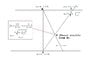
Remember that I said event E and event O are, by definition (or perhaps by construction) *simultaneous* in the ECC frame. That means event E is the event on the second observer's worldline that would be assigned the same time coordinate in the ECC frame as event O; in other words, event E is the event at which the Earth observer's "surface of simultaneity" at event O intersects the second observer's worldline. So the "speed of light delay" is already taken into account (at least, I think that's how you're using the term).

However, the way the ECC frame is constructed, its "surface of simultaneity" at event O exactly matches the (Euclidean) surface of constant cosmological time t = 13.7 billion years in the FRW frame, the (curved) spacetime metric in which cosmology is normally done. So according to the FRW frame, the second observer's proper time since the big bang at event E will be *exactly* 13.7 billion years, *not* 13.65 billion years.

 

[JDoolin]

So we have what I'll call the "Earth-centered cosmological" (ECC) reference frame, which is the local inertial frame of this observer just passing Earth now that sees the CMBR as isotropic, so his only "motion" is due to the expansion of the Universe. Now consider a similar observer a million parsecs from Earth (distance "now" as measured in the ECC frame). The current estimate of the Hubble constant is about 70 km/sec per million parsecs, so this second observer, in the ECC frame, would appear to be moving away from Earth at 70 km/sec. Pick the event on the second observer's worldline that has the time coordinate "now" according to the ECC frame, and call that event E; the origin of the ECC frame will be the event of Earth "now", which we'll call event O.

Now consider the following: the time since the Big Bang at event O, according to the ECC frame, is 13.7 billion years. How much proper time has the second observer experienced since the Big Bang at event E? The problem is that the "obvious" answer in the ECC frame is *wrong*. The obvious answer is that, since the second observer is moving in the ECC frame, time dilation will make his proper time since the Big Bang at event E *less* than the Earth's proper time since the Big Bang at event O. However, the actual general relativistic cosmological models that best match the data say that the second observer's proper time since the Big Bang at event E will be the *same* as the Earth's proper time since the Big Bang at event O.

You've double-defined event O. Saying that both the big bang is "O" and Earth now is "O." I want to define four events. You've defined "E" as the "the event on the second observer's worldline that has the time coordinate "now" according to the ECC frame" That one is good. The other events I'm defining are:

O: The Big Bang.
N: The event of here and now. Earth Circa 2010, 13.7 billion years after O.
P: The event that we are currently seeing, looking at the galaxy that is moving along a path from O to E.

Now, in my previous post, I only considered what to expect out to about 1.3 billion light years. And I only gave lip-service to the speed-of-light delay. In this post, I want to make "The obvious answer" a little more complete. Specifically, I think the "obvious answer" out to 1.3 billion light years is pretty close to what we see. It is out beyond 6 billion light years where the "obvious answer" is clearly wrong.

Here is the problem with the "obvious answer". If you are observing galaxies out beyond 7 billion light years (which we do), (Event P at 7 billion light years--Event E at 14 billion light years, it means that the velocity of those stars is greater than the speed of light. If this "obvious answer" were correct, we should not see any stars beyond 7 billion light years distance.

However, we see here:

http://www.astro.ucla.edu/~wright/sne_cosmology.html

We have supernovae all the way out to 12 giga-parsecs (39 billion light years.) That means the "obvious" answer cannot be right. It should be noticed though, that this is under the assumption that the hubble-constant is a global parameter. A careful analysis of the graph indicates that hubble's constant is 70 km/s per megaparsec in a region nearby, out to about 6 billion light years, but seems to be much smaller as you go out beyond that region.

 

[Mentz114]

The big bang didn't happen 'somewhere'. It was 'everywhere'. So you're free to choose any point as the 'center', and choosing the point you're at is most convenient. ( sorry about all the 'quotes', but it's a subtle distinction).

 

[JDoolin]

Remember that I said event E and event O are, by definition (or perhaps by construction) *simultaneous* in the ECC frame. That means event E is the event on the second observer's worldline that would be assigned the same time coordinate in the ECC frame as event O; in other words, event E is the event at which the Earth observer's "surface of simultaneity" at event O intersects the second observer's worldline. So the "speed of light delay" is already taken into account (at least, I think that's how you're using the term).

I posted, and then saw you had posted. I'm still not quite sure how the event E takes into account the speed-of-light delay. Hopefully the diagram I drew, which includes point P will show what I mean by taking into account the speed of light delay.

The event E which intersects the Earth observer's "surface of simultaneity" will not be seen on Earth for a long, long time. However, the event P which intersects the observer's "past light cone" is what is seen on Earth NOW.

 

[JDoolin]

The big bang didn't happen 'somewhere'. It was 'everywhere'. So you're free to choose any point as the 'center', and choosing point you're at is most convenient. ( sorry about all the 'quotes', but it's a subtle distinction).

PeterDonis brought up the idea of an ECC, Earth Centered Cosmological frame, in which the anisotropy of the CMBR disappeared. It appears that if we adjusted our velocity by about 600 km/second, in the appropriate direction, then we would be able to make this anisotropy disappear.

I would agre that once we did this, then a "point" in our space-ship is an actual center of the universe. Since we're free to set off that space-ship at any time we want, and any place we want, we can choose any event to be the center of the universe. But if we choose a point, we have to choose a specific velocity as well. A "point" in space, is a worldline in space-time.

Now, the interpretation of General Relativistic Cosmology is that all of these cosmologically centered worldlines are parallel (or at least they don't cross). The divergence of those cosmologically centered worldlines is not due to real motion of the particles. It is due, instead to an increasing scale factor. In the past, that scale factor goes right down to zero. However, the unscaled distance remains more-or-less the same throughout time.

This is how I have come to understand the idea, though I realize that perhaps my understanding is not complete.

But how can I reconcile this with my idea that the big bang happened "somewhere." Honestly, I don't think I can. If you trace back a set of straight lines to where they intersect, you get a "somewhere" But if you trace back a set of lines that curve, and do not cross, then you get an "everywhere". My diagram in post 37 assumes that the two lines do cross somewhere in the past. Is there any chance that we could even use this as an approximation? That we could maybe just "pretend" that two galaxies traveling at velocity away from each other were once, far in the past at the same place, at the same time? I guess we wouldn't have to call it the big bang; just the meeting event. And maybe they never met, but just assume that the majority of the time they were moving away from each other, they acted as though they met.

 

[Mentz114]

I think you are on the right track. If the big-bang started at a singularity, then all the constituents that make up the universe were once in same place ( the only place) at t=0.

I don't have time to reply to this at length, but this document says it much better, and has loads of good diagrams.

http://ls.poly.edu/~jbain/philrel/philrellectures/12.RelativisticCosmology.pdf

 

[JDoolin]

I think you are on the right track. If the big-bang started at a singularity, then all the constituents that make up the universe were once in same place ( the only place) at t=0.

I don't have time to reply to this at length, but this document says it much better, and has loads of good diagrams.

http://ls.poly.edu/~jbain/philrel/philrellectures/12.RelativisticCosmology.pdf

The attached diagrams came from the referenced article. They both are graphs of space vs. time. The Robertson Walker diagram has elements that go to infinite speed. The "conformal" version has all elements stationary. Are these two diagrams supposed to be different diagrams of the same thing, or are they different geometries in the same coordinates?

Is the time parameter in the Robertson Walker diagram supposed to be proper time of particles, or does it represent coordinate time for a hypothetical observer?

 

[Mentz114]

The attached diagrams came from the referenced article. They both are graphs of space vs. time. The Robertson Walker diagram has elements that go to infinite speed. The "conformal" version has all elements stationary. Are these two diagrams supposed to be different diagrams of the same thing, or are they different geometries in the same coordinates?

Same geometry, different coords.

Is the time parameter in the Robertson Walker diagram supposed to be proper time of particles, or does it represent coordinate time for a hypothetical observer?

Those diagrams illustrate the horizon that exists in an expanding FRW universe. The first diagram uses scaled coordinates, so everything starts in the same place and remains the same distance apart. The straight red lines represent horizons. As time progresses, each worldline loses touch with the others as they move outside its future light cones.

In the second diagram, comoving coordinates are used, so we can pick any worldline as our reference frame. In these coords all the other matter appears to be receding. The horizon lines now become the red curves. I think the point is that the physics is the same whichever of these coords we use.

I haven't got time to do it right now but I'll get the actual transformations and post them.

Is the time parameter in the Robertson Walker diagram supposed to be proper time of particles, or does it represent coordinate time for a hypothetical observer?

In both diagrams, the vertical axis is coordinate time.

 

[PeterDonis]

Is the time parameter in the Robertson Walker diagram supposed to be proper time of particles, or does it represent coordinate time for a hypothetical observer?

I'm not sure what "coordinate time for a hypothetical observer" means. The Robertson-Walker coordinates are constructed in such a way that coordinate time directly represents the proper time of observers who are "at rest" in those coordinates--in other words, observers whose values of the spatial coordinates remain constant (and who see the universe as isotropic for all time). As you noted, the actual proper distance between any two such observers increases with time because of the increase of the scale factor; this is a more precise way of saying that the universe is "expanding".

The "conformal" coordinates in the other diagram can be constructed from the Robertson-Walker coordinates in two steps, which I'll describe here in highly "heuristic" fashion: (1) take the initial singularity, which is a point (a single event), and "stretch it out" into a line; (2) take the Robertson-Walker time coordinate and "stretch" it by an amount that increases as the singularity is approached, so that after the stretching is done, all light rays travel on 45 degree lines. This makes it easy to see the causal structure of the spacetime.

 

[PeterDonis]

You've double-defined event O. Saying that both the big bang is "O" and Earth now is "O."

I didn't mean to double-define O; I meant O to always refer to the Earth now. Sorry if I wasn't clear.

Here is the problem with the "obvious answer". If you are observing galaxies out beyond 7 billion light years (which we do), (Event P at 7 billion light years--Event E at 14 billion light years, it means that the velocity of those stars is greater than the speed of light. If this "obvious answer" were correct, we should not see any stars beyond 7 billion light years distance.

However, we see here:

http://www.astro.ucla.edu/~wright/sne_cosmology.html

We have supernovae all the way out to 12 giga-parsecs (39 billion light years.) That means the "obvious" answer cannot be right. It should be noticed though, that this is under the assumption that the hubble-constant is a global parameter. A careful analysis of the graph indicates that hubble's constant is 70 km/s per megaparsec in a region nearby, out to about 6 billion light years, but seems to be much smaller as you go out beyond that region.

This is what I was referring to as the curvature of the FRW spacetime: as you go back in time, the local inertial frames on a given worldline (say, that of the cosmological observer who is at Earth's spatial location now) don't "line up" with each other. The changing slope of the graph is evidence of that.

 

[PeterDonis]

Hopefully the diagram I drew, which includes point P will show what I mean by taking into account the speed of light delay.

Yes, it's clear, and it matches what I understood you to be saying. Event E is spacelike separated from the event you've labeled N, but that doesn't prevent us from calculating the proper time between the big bang (which you've labeled O) and event E, along the "straight" worldline connecting them. As we've seen, that calculation gives an answer which can't be right.

 

[JDoolin]

In the conformal map (see post 42, above), the light rays are always parallel to the light cones. In the Robertson Walker coordinates, the light rays don't follow the light cones. Is there a mistake in one of the diagrams?

The light rays come to a full stop in the Robertson Walker diagram, stopping and turning around and coming the opposite direction. Is that expected?

(Now I see, Mentz post #43, the lines are not light rays but horizon lines? I'm not quite clear on what that means.)

 

[PeterDonis]

In the conformal map, the light rays are always parallel to the light cones. In the Robertson Walker coordinates, the light rays don't follow the light cones. Is there a mistake in one of the diagrams?

The light rays come to a full stop in the Robertson Walker diagram, stopping and turning around and coming the opposite direction. Is that expected?

Yes, it's expected, and no, there's no mistake in the diagrams. The light rays actually do follow the light cones in the Robertson Walker coordinates, but it's hard to see because the bottom of the diagram is crunched together (that's one of the reasons conformal coordinates are useful). The two opposite "sides" of the past light cone actually originate from the *same* event, the initial singularity (since everything originates there), but they "come out" in different directions that aren't quite opposite--there's a little bit of "tilt" in each ray towards the other one. As the expansion of the universe decelerates, and the light cones tilt inward (until they're vertical at "now"), the two light rays are bent back together to meet at "here and now".

Part 3 of Ned Wright's cosmology tutorial at http://www.astro.ucla.edu/~wright/cosmo_03.htm gives more details about these diagrams.

 

[JDoolin]

Yes, it's clear, and it matches what I understood you to be saying. Event E is spacelike separated from the event you've labeled N, but that doesn't prevent us from calculating the proper time between the big bang (which you've labeled O) and event E, along the "straight" worldline connecting them. As we've seen, that calculation gives an answer which can't be right.

So does it seem to you that if we go out to about one or two billion light years that we have what appears to fit a Minkowski approximation, and then only once you get out past 6 billion light years does it seem that the space is noticeably stretching? Because if you agree with me that this is essentially the case, then I can begin to discuss the invisible elephant in the room, which is acceleration.

The "obvious" calculation we're doing makes the assumption of a uniform, peaceful expansion at the beginning of the universe. This is highly unlikely, because one should expect nuclear explosions, or matter-anti-matter explosions, of great force (or possibly even greater unknown particle-interactions) in the instants immediately after the big bang.

I don't know how to treat these interactions in General Relativity, but I do have some idea how to treat them in Minkowski spacetime. You've seen that the calculation without acceleration cannot be right. Would you humor me long enough to see that the calculation with acceleration actually could be right?

 

[PeterDonis]

So does it seem to you that if we go out to about one or two billion light years that we have what appears to fit a Minkowski approximation, and then only once you get out past 6 billion light years does it seem that the space is noticeably stretching?

I don't know that I disagree, but I don't know that I would put it this way either. The "stretching" doesn't happen in space; it happens in time, as the scale factor changes. Obviously you can kind of convert time to space because looking farther away means looking at things the way they were a longer time ago; but I'm not sure I would characterize what we see as we look out that far as "stretching". Maybe my further comments below will help to clarify what I'm getting at.

Because if you agree with me that this is essentially the case, then I can begin to discuss the invisible elephant in the room, which is acceleration.

We have to be careful with terminology here as well, because the cosmological observers we've been discussing (the ones at rest in the Robertson-Walker coordinates) are not accelerating; that is, they don't feel any acceleration. And again, I'm not sure that the fact that the local inertial frames of cosmological observers at different times don't "line up" is most usefully viewed as an "acceleration", although that term is often used (as in, the expansion of the universe is now accelerating, but was decelerating earlier in its history).

The "obvious" calculation we're doing makes the assumption of a uniform, peaceful expansion at the beginning of the universe. This is highly unlikely, because one should expect nuclear explosions, or matter-anti-matter explosions, of great force (or possibly even greater unknown particle-interactions) in the instants immediately after the big bang.

I don't know how to treat these interactions in General Relativity, but I do have some idea how to treat them in Minkowski spacetime. You've seen that the calculation without acceleration cannot be right. Would you humor me long enough to see that the calculation with acceleration actually could be right?

The calculations we've been doing are kinematic; they don't get into the detailed dynamics of what's going on with the matter-energy in the universe. The Robertson-Walker models abstract all that out by treating the matter-energy in the universe as a perfect fluid, which can take one of three simple forms characterized by different equations of state relating the pressure, p, to the energy density, rho:

(1) "Matter dominated": a fluid with zero pressure, p = 0. This is a good approximation at the cosmological level for non-relativistic matter (meaning, the average speed of the individual "particles" in the fluid, which are basically galaxies or galaxy clusters, is much less than the speed of light).

(2) "Radiation dominated": a fluid with equation of state p = 1/3 rho. This is the equation of state for a "fluid" made of pure radiation (for example, the CMBR).

(3) "Vacuum dominated": a fluid with equation of state p = - rho. This is the equation of state for a "fluid" which is due to a cosmological constant (other terms used are "vacuum energy" or "dark energy").

The current best fit model for the evolution of the universe is: first the "inflation" phase, in which the equation of state was vacuum dominated with an extremely large effective energy density rho, meaning that the universe "expanded" exponentially; then, after the phase transition that ended inflation, a radiation dominated phase, which lasted roughly until the time of "recombination" (electrons and nuclei combining into atoms, which made the universe basically transparent to photons) when the universe was about 100,000 years old (all these times are very approximate, I'm going from memory here); then a matter dominated phase, which lasted until a few billion years ago (I believe); and finally, another vacuum dominated phase but with a very, very small effective energy density, causing the expansion of the universe to start "accelerating" again (it had been decelerating during the radiation and matter dominated phases).

The reason I go into all this is to illustrate that nowhere in any of this did I have to specify what, exactly, was going on *within* the cosmological fluid, in terms of nuclear reactions, explosions, whatever. The only thing that matters for the overall dynamics of the universe is the equation of state, and the effective equation of state of the cosmological fluid, on an overall level, can remain the same while the fluid undergoes violent internal changes. (Part of how this can work is that the identity of the individual "particles" that compose the fluid changes over time: in the early universe, they were elementary particles like quarks, electrons, and photons; then they were atoms of hydrogen, helium, and a few other elements; and for the past few billion years, at least, they've been galaxies and galaxy clusters. But on a gross cosmological level, all of these different "fluids" can be described by the same simple equations of state I gave above.)

So as far as the overall dynamics of the universe is concerned, we can get away with *not* modeling all the details you mention. (We do have to model them, at least to some extent, in order to predict finer details like the ratios of abundances of different elements that we should expect to see in intergalactic space.) Another way of saying this is that, in fact, the Robertson-Walker models do *not* make the assumption of a "peaceful" expansion of the early universe; they only make the assumption that, whatever might be going on at a detailed level, it can be adequately modeled at an overall level by a fluid with one of the above equations of state. That assumption appears to be working pretty well so far.

I'm not sure if you want to get into the actual derivation of the Robertson-Walker metric; the Wikipedia page, http://en.wikipedia.org/wiki/Friedmann–Lemaître–Robertson–Walker_metric, has a decent (if brief) discussion. Also, technically, these models do not go all the way back to the initial singularity (the word "singularity" means the equations break down and the model can't make predictions). Currently the actual models, as I understand it, more or less assume that the inflation phase started with a state the size of the Planck length or thereabouts (not a zero-size initial singularity), which began expanding exponentially; how that state came to be is not known, though there are various proposals with no real way of testing any of them experimentally at this time.

 

[JDoolin]

Yes, it's expected, and no, there's no mistake in the diagrams. The light rays actually do follow the light cones in the Robertson Walker coordinates, but it's hard to see because the bottom of the diagram is crunched together (that's one of the reasons conformal coordinates are useful). The two opposite "sides" of the past light cone actually originate from the *same* event, the initial singularity (since everything originates there), but they "come out" in different directions that aren't quite opposite--there's a little bit of "tilt" in each ray towards the other one. As the expansion of the universe decelerates, and the light cones tilt inward (until they're vertical at "now"), the two light rays are bent back together to meet at "here and now".

Part 3 of Ned Wright's cosmology tutorial at http://www.astro.ucla.edu/~wright/cosmo_03.htm gives more details about these diagrams.

Mea Culpa. I did not notice that on the lower triangles both the left side and the right side are going in the same direction.

Thank you for the link to Ned Wright's page, but that leads me to further questions. Earlier, I was saying that I did not know how to handle acceleration in general relativiy. Ned Wright handles a change-of-reference frames in the GR by doing a Galilean Transformation (attached)

http://www.astro.ucla.edu/~wright/cosmo_03.htm]Note[/PLAIN] that this is not a Lorentz transformation, and that these coordinates are not the special relativistic coordinates for which a Lorentz transformation applies. The Galilean transformation which could be done by skewing cards in this way required that the edge of the deck remain straight, and in any case the Lorentz transformation can not be done on cards in this way because there is no absolute time. But in cosmological models we do have cosmic time, which is the proper time since the Big Bang measured by comoving observers, and it can be used to set up a deck of cards. The presence of gravity in this model leads to a curved spacetime that can not be plotted on a flat space-time diagram without distortion. If every coordinate system is a distorted representation of the Universe, we may as well use a convenient coordinate system and just keep track of the distortion by following the lightcones.

I'm not sure what he's saying, but he seems to be saying that since Lorentz Transformation does not apply to these coordinates, that Galilean Transformation actually DOES apply. Also, this suggests that the vertical component of the graph is NOT the coordinate time of the central observer, but rather it is the "cosmological time" which is the "proper time since the Big Bang measured by comoving observers."

So effectively, you're doing a velocity transformation, but it is unusable as acceleration, because the two reference frames are "comoving."

So my question is, if you want to handle a real acceleration; how is this handled? I presume it is not done by either galilean transformation or by lorentz transformation.

We have to be careful with terminology here as well, because the cosmological observers we've been discussing (the ones at rest in the Robertson-Walker coordinates) are not accelerating; that is, they don't feel any acceleration. And again, I'm not sure that the fact that the local inertial frames of cosmological observers at different times don't "line up" is most usefully viewed as an "acceleration", although that term is often used (as in, the expansion of the universe is now accelerating, but was decelerating earlier in its history).

I know RW coordinates are not accelerating. The question is whether they can handle acceleration. And I'm not talking about gravitational acceleration. I'm talking about acceleration due to the pressure caused by primordial particles decaying, creating pressure, reaching critical mass, exploding, etc. One can handle these accelerations in Minkowski space-time rather easily. But in R-W coordinates, it appears that Lorentz Transformation will not do the job. So will Galilean Transformation do it?

 

[JDoolin]

I don't know that I disagree, but I don't know that I would put it this way either. The "stretching" doesn't happen in space; it happens in time, as the scale factor changes. Obviously you can kind of convert time to space because looking farther away means looking at things the way they were a longer time ago; but I'm not sure I would characterize what we see as we look out that far as "stretching". Maybe my further comments below will help to clarify what I'm getting at.



We have to be careful with terminology here as well, because the cosmological observers we've been discussing (the ones at rest in the Robertson-Walker coordinates) are not accelerating; that is, they don't feel any acceleration. And again, I'm not sure that the fact that the local inertial frames of cosmological observers at different times don't "line up" is most usefully viewed as an "acceleration", although that term is often used (as in, the expansion of the universe is now accelerating, but was decelerating earlier in its history).

Actually, I'm not quite sure what you mean by observer's lining up.

The calculations we've been doing are kinematic; they don't get into the detailed dynamics of what's going on with the matter-energy in the universe. The Robertson-Walker models abstract all that out by treating the matter-energy in the universe as a perfect fluid, which can take one of three simple forms characterized by different equations of state relating the pressure, p, to the energy density, rho:

(1) "Matter dominated": a fluid with zero pressure, p = 0. This is a good approximation at the cosmological level for non-relativistic matter (meaning, the average speed of the individual "particles" in the fluid, which are basically galaxies or galaxy clusters, is much less than the speed of light).

(2) "Radiation dominated": a fluid with equation of state p = 1/3 rho. This is the equation of state for a "fluid" made of pure radiation (for example, the CMBR).

(3) "Vacuum dominated": a fluid with equation of state p = - rho. This is the equation of state for a "fluid" which is due to a cosmological constant (other terms used are "vacuum energy" or "dark energy").

I don't understand the idea of a pressure less than zero. Also, what is rho?

The current best fit model for the evolution of the universe is: first the "inflation" phase, in which the equation of state was vacuum dominated with an extremely large effective energy density rho, meaning that the universe "expanded" exponentially; then, after the phase transition that ended inflation, a radiation dominated phase, which lasted roughly until the time of "recombination" (electrons and nuclei combining into atoms, which made the universe basically transparent to photons) when the universe was about 100,000 years old (all these times are very approximate, I'm going from memory here); then a matter dominated phase, which lasted until a few billion years ago (I believe); and finally, another vacuum dominated phase but with a very, very small effective energy density, causing the expansion of the universe to start "accelerating" again (it had been decelerating during the radiation and matter dominated phases).

To me, it seems like there should be a radioactive decay dominated era. You have a matter-dominated era, where the particles are not, on average, old enough to have decayed. Then particle start decaying, and the pressure builds, and you have cascading reactions. This would have, on average, a pressure far beyond the pressure in the radiation dominated era. Also, the net effect of these interactions would be to mash the matter in the universe together, providing the seeds for stars and galaxies.

In the attachment, I took the liberty of modifying the RW diagram to show worldlines of particles flying out of a "secondary bang" imagining some region where a large number of particles reached critical density at the same time, producing an enormous reaction.

If we don't have a good explanation already for our 600 km/s peculiar velocity with the CMBR, this could explain it. Also, this would explain why nearby, we have a hubble's constant of 70 km/s per megaparsec, and further out we have a much smaller Hubble constant.

 

[PeterDonis]

I know RW coordinates are not accelerating. The question is whether they can handle acceleration. And I'm not talking about gravitational acceleration. I'm talking about acceleration due to the pressure caused by primordial particles decaying, creating pressure, reaching critical mass, exploding, etc. One can handle these accelerations in Minkowski space-time rather easily. But in R-W coordinates, it appears that neither Lorentz Transformation will not do the job. So will Galilean Transformation do it?

Wright calls the transformation he uses a "Galilean transformation" because, loosely speaking, it doesn't "change the time direction" the way a Lorentz transformation does; it leaves the surfaces of constant cosmological time invariant, and just transforms the space coordinates within each surface. In General Relativity, this kind of transformation is perfectly legitimate, as long as you transform *everything* accordingly. It just so happens that this particular transformation, in addition to leaving the surfaces of constant cosmological time invariant, also preserves the isotropy of space--the fact that everything looks the same in all directions. So it actually leaves the entire Robertson-Walker metric invariant; the metric looks exactly the same in the transformed coordinates as it does in the original coordinates.

This means that, for example, the cosmological observers--the ones "at rest" in the Robertson-Walker coordinates--are still not accelerating in the transformed coordinates; all that's changed is which particular set of constant space coordinates each observer is at. So I think the simple answer to your question is that Wright's "Galilean transformation" is not intended to "handle accelerations".

However, as I said in my previous post, I don't think a model of the universe as a whole is meant to handle accelerations in the sense you mean, because it simply doesn't model things to that level of detail. See my next post responding to your next post for more on this, since it fits in better in response to what you said in that post.

 

[PeterDonis]

Actually, I'm not quite sure what you mean by observer's lining up.

I mean that the local inertial frames at, say, the event you labeled N (the Earth now), and another event P, a point on the worldline of the cosmological observer that passes through N, but ten billion years to the past of N (according to that observer's proper time) are different inertial frames, the same way that the inertial frames of observers moving at different velocities are different inertial frames. If we extended both local inertial frames far enough in time that they overlapped, their coordinate lines would not line up, just as the coordinate lines of observers moving at different velocities do not line up.

I don't understand the idea of a pressure less than zero. Also, what is rho?

Ned Wright has a page that explains briefly how the negative pressure of the vacuum works here: http://www.astro.ucla.edu/~wright/cosmo_constant.html.

Rho is the energy density of the cosmological fluid, as seen by an observer at rest in the cosmological coordinates. Some people write $\rho$ to mean the mass density, so the energy density would then be $\rho c^{2}$; I like to work in units where c = 1, so energy density and mass density are the same thing.

To me, it seems like there should be a radioactive decay dominated era. You have a matter-dominated era, where the particles are not, on average, old enough to have decayed. Then particle start decaying, and the pressure builds, and you have cascading reactions. This would have, on average, a pressure far beyond the pressure in the radiation dominated era. Also, the net effect of these interactions would be to mash the matter in the universe together, providing the seeds for stars and galaxies.

What you say about pressure here isn't right. The pressure in the radiation dominated equation of state is actually a limiting case of the pressure due to highly relativistic particles, which is what would be produced by reactions such as you describe. Basically, as the particles in the fluid become more relativistic, the pressure builds from zero (the non-relativistic limiting case) to 1/3 rho (the relativistic limiting case).

I believe you're correct, though, that internal reactions in the cosmological fluid would have the effect of producing "clumps" of higher density, which would then contract gravitationally to form stars and galaxies. I don't know offhand how large this effect is believed to be compared with the effect of "primordial density fluctuations", which are basically quantum fluctuations in the initial state at the beginning of the inflation phase, magnified by many orders of magnitude during the inflation.

In the attachment, I took the liberty of modifying the RW diagram to show worldlines of particles flying out of a "secondary bang" imagining some region where a large number of particles reached critical density at the same time, producing an enormous reaction.

Again, I believe this is basically correct, but I don't know how large an effect it would be compared to others. The only caveat I can see is that, because the universe is expanding, there may be limits on how high the density and pressure can get in such a localized "bang" compared to what they were in the actual initial "bang".

If we don't have a good explanation already for our 600 km/s peculiar velocity with the CMBR, this could explain it. Also, this would explain why nearby, we have a hubble's constant of 70 km/s per megaparsec, and further out we have a much smaller Hubble constant.

I agree your suggestion could in principle explain the peculiar velocity of a particular system of matter now (e.g., the solar system). The variation in the Hubble constant, however, is due to the change in the expansion rate of the universe, and is already accounted for in the basic Robertson-Walker models. (Different models predict different specific "curvatures" in the diagram, but they all predict *some* curvature.)

 

[Mentz114]

JDoolin, you should be aware that the FRW model is an large scale approximation whose symmetries are isotropy and homogeneity. On a smaller scale than cosmic we know that clusters of galaxies have peculiar ( ie not Hubble flow) motions and galaxies within clusters also have this kind of motion, superimposed on the flow. PeterDonis makes this point also.

GR allows us to write models of the whole universe and also to work out how this universe would look to different observers, which is where the coordinate transformations come in. A great benefit is that the essential physics and symmetries of the model will not be lost when we do coordinate transforms. You've seen two examples in FRW spacetime. The one that corresponds best to our experience is the comoving frame which sees all other matter as receding with cosmological red-shift.
It's also possible to define a frame where clock rates change with time so everything looks static.

I think my point is - some of your questions, good though might be, are outside the range of what GR can tell us.

On the question of Gallilean vs Lorentz transformations - this depends on what geometry you choose for your 3D hyperslices, when making a transformations. As you can see in the lecture notes, there are Euclidean ( Galliean relativity) or hyperbolic ( SR) as possibilities. No doubt the coords Ned Wright was using had Euclidean spatial hyperslices (Painleve coords, probably).

 

[PeterDonis]

No doubt the coords Ned Wright was using had Euclidean spatial hyperslices (Painleve coords, probably).

No, Painleve coordinates apply to the Schwarzschild spacetime. Wright was using the Robertson-Walker coordinates for the critical density case, where the spatial slices are Euclidean. Wright doesn't specifically write down the metric in the coordinates he's using, but I believe it would look like this:

$$d\tau^{2} = dt^{2} - a(t) \left[ dr^{2} + r^{2} \left( d\theta^{2} + sin^{2} \theta d\phi^{2} \right) \right]$$

Every "cosmological observer" has constant spatial coordinates r, theta, phi in this coordinate system; and it should be obvious from the metric above that the time coordinate t directly reflects the proper time experienced by these observers. All the time variation (the "expansion" of the universe), and hence all the curvature of spacetime, is reflected in the dynamics of the scale factor a(t).

The spatial coordinate in Wright's "Galilean transformation" diagram would be r in the metric above; his transformation is basically just a spatial translation to put a different cosmological observer at the origin r = 0.

 

[Mentz114]

No, Painleve coordinates apply to the Schwarzschild spacetime.

Yes, there is a Painleve chart for FRW dust. Do you want me to post it ?

Every "cosmological observer" has constant spatial coordinates r, theta, phi in this coordinate system; and it should be obvious from the metric above that the time coordinate t directly reflects the proper time experienced by these observers.

Phew - how can say that when you've just seen two different coordinate transformations of FRW representing observer frames with completely different proper times ?

 

[PeterDonis]

Yes, there is a Painleve chart for FRW dust. Do you want me to post it ?

Yes, please.

Phew - how can say that when you've just seen two different coordinate transformations of FRW represnting observer frames with completely different proper times ?

Just read it off the metric I wrote: for an observer at rest in the spatial coordinates, dr = dtheta = dphi = 0. So the metric reads $d\tau^{2} = dt^{2}$. Any transformation that leaves the metric in the same form (which, as I understand it, Wright's "Galilean transformation" does) will preserve that property. But of course, a transformation into some other coordinates where the metric looks different (such as Wright's "special relativistic" coordinates) may not.

 

[Mentz114]

Just read it off the metric I wrote: for an observer at rest in the spatial coordinates, dr = dtheta = dphi = 0. So the metric reads $d\tau^{2} = dt^{2}$. Any transformation that leaves the metric in the same form (which, as I understand it, Wright's "Galilean transformation" does) will preserve that property. But of course, a transformation into some other coordinates where the metric looks different (such as Wright's "special relativistic" coordinates) may not.

You're right about the raw coordinates, no transformation is needed because it the spatial slice is already conformally flat. I didn't read your post properly. Anyhow, I did put a 'probably' after my Painleve speculation

I'll look up the Painleve chart as soon as my coffee is brewed and consumed.

 

[Mentz114]

FRW in Painleve chart

I had a problem editing my previous post so I made a new one.

$$\begin{align*} dt_p&=dt\\ dx_p&=dx-\frac{2\,x}{3\,t}dt\\ dy_p&=dy-\frac{2\,y}{3\,t}dt\\ dz_p&=dz-\frac{2\,z}{3\,t}dt \end{align*}$$

which gives a metric,

$$\left[ \begin{array}{cccc} \frac{4\,{z}^{2}+4\,{y}^{2}+4\,{x}^{2}-9\,{t}^{2}}{9\,{t}^{2}} & -\frac{2\,x}{3\,t} & -\frac{2\,y}{3\,t} & -\frac{2\,z}{3\,t}\\\ -\frac{2\,x}{3\,t} & 1 & 0 & 0\\\ -\frac{2\,y}{3\,t} & 0 & 1 & 0\\\ -\frac{2\,z}{3\,t} & 0 & 0 & 1 \end{array} \right]$$
The spatial part is static now.

The Einstein tensor transformed by this frame field has only one non-zero component,
$$G_{00}=\frac{4}{3\,{t}^{2}}$$
which up to a factor is the SET of static non-interacting dust whose density varies with time. The Riemann scalar is $80/27t^4$ which shows there is an unremoveable curvature singularity at $t=0$.

 

[JDoolin]

I'm a little troubled that the Robertson Walker chart is either mapping coordinate time or proper time, depending on who gives me an answer. If it is supposed to be proper time, then I understand what you mean by events "not lining up" The problem is that the intersection of two world-lines on a space versus proper time graph do not indicate co-location in space (a collision).

If the diagram represents space vs. proper time, also, this casts into doubt the presence of the light-cones *anywhere* in the diagram. Light does not age, and therefore it should not move forward in proper time. All the light rays in a space vs. proper time diagram should be horizontal. And the intersection of light rays and world-lines on the space versus proper time diagram are all but meaningless. (since as mentioned before, they don't "line up")

PeterDonis told me that Lewis Epstein was encouraging the confusion of proper time and coordinate time, but it appears to me that Robertson Walker have already successfully muddled the two. Epstein, in fact, made great strides in clarifying the difference.

 

[Mentz114]

I'm a little troubled that the Robertson Walker chart is either mapping coordinate time or proper time, depending on who gives me an answer.

I'm not sure what you mean by 'chart' or 'mapping'. Care to elaborate ?

The problem is that the intersection of two world-lines on a space versus proper time graph do not indicate co-location in space (a collision).

The coincidence of worldlines always means collision. Same place, same time. No transformation can change that.

Coordinate time is a parameter in the model, proper time is the integral of the Lorentzian interval along a worldline.

 

[JDoolin]

I'm not sure what you mean by 'chart' or 'mapping'. Care to elaborate ?


The coincidence of worldlines always means collision. Same place, same time. No transformation can change that.

Coordinate time is a parameter in the model, proper time is the integral of the Lorentzian interval along a worldline.

It's my question in post #42. You're sometimes saying that the vertical coordinate in the Robertson-Walker diagram represents the proper time of particles. Other times, you're acting like it is the actual time passed by the central observer. You can either have one or the other. Not both.

The only place where those two definitions can be shared is along the single line representing the worldline of the "stationary" particle.

As I've pointed out before, the parameters of $\tau$ and t are very different. In an x vs t diagram, you are correct. The coincidence of worldlines always mean a collision, and no legitimate transformation can change that...EXCEPT FOR a transformation into an x vs $\tau$ coordinate system, which is totally NOT a legitimate transformation, because $\tau$ is not a coordinate. It is a property of matter.

And when two pieces of matter cross the same coordinate space, when they reach the same PROPER AGE, that does NOT mean that they are colliding. It means they just happened to reach that same spot in space when they happened to be the same proper age. That does NOT mean they reached the same spot at the same TIME.

So, I repeat, (more emphatically, this time,) that an intersection on a space vs proper time graph, is all but physically meaningless.

 

[Mentz114]

OK.

On a spacetime diagram, the vetical axis is t, coordinate time. For the vertical worldline we can calculate the proper time on the clock,

$$d\tau^2=dt^2-dx^2=dt^2 \Rightarrow d\tau=dt$$

because dx=0. For the tilted worldlines we get a different proper time. So every observer thinks his clock is showing coordinate time. Can you see why people say that the vertical axis shows proper time ? Because for the stationary observer it does. None of this is of the least significance. Assume that in a spacetime diagram it is t vs x.

 

[JDoolin]

OK.

On a spacetime diagram, the vetical axis is t, coordinate time. For the vertical worldline we can calculate the proper time on the clock,

$$d\tau^2=dt^2-dx^2=dt^2 \Rightarrow d\tau=dt$$

because dx=0. For the tilted worldlines we get a different proper time. So every observer thinks his clock is showing coordinate time. Can you see why people say that the vertical axis shows proper time ? Because for the stationary observer it does. None of this is of the least significance. Assume that in a spacetime diagram it is t vs x.

This is why I'm saying I get different answers depending on who answers. http://www.astro.ucla.edu/~wright/cosmo_03.htm" "But in cosmological models we do have cosmic time, which is the proper time since the Big Bang measured by comoving observers, and it can be used to set up a deck of cards."

It has to be proper time that he's talking about, because, he then proceeds to do a Galilean Transformation on the diagram. The reason that it's valid to do this transformation is that the horizontal lines in the diagram represent lines of constant PROPER time. (Specifically, proper time for particular observers, who are following particular worldlines.)

While I have no objection to graphing proper time vs. position, this way, I think we deserve a certain amount of clarity about which is being graphed, because it can be either one or the other, but not both. If we have a space vs. proper-time graph, the speed of light should be represented as horizontal lines; not light cones. If we have a space vs TIME graph, then it is not valid to do a galilean transformation, because the relativity of simultaneity has to come into play.

(I don't know what you do, when the Lorentz Transformations are only valid "locally" but you need to have some kind of transformation that looks like the Lorentz Tranformations locally, and whatever they do with the rest of the stretching space, I really cannot say.)

 

[Mentz114]

I can see why you're confused. The FRW model is special in this way - because of the homogenity and isotropy, every worldline is the same.

While this diagram is drawn from our point-of-view, the Universe is homogeneous so the diagram drawn from the point-of-view of any of the galaxies on the diagram would be identical.

From my previous post you can see that for the stationary observer proper time and coordinate time coincide. Now combine that with the quote above, and one concludes that all the observers' clocks are showing coordinate time.

Ned Wright says 'we do not have absolute time', which I find puzzling, but we do have 'cosmic time', which coincides with any observer if we choose them to be at rest ( vertical wl). But coordinate time also has the property that it coincides with the stationary clock time. Therefore cosmic time = coordinate time, as far as I can see.

Looking at the spacetime diagram that shows all the worldines as straight and radiating from t=0, r=0. In a Minkowski diagram, those lines should all be curving away from the central stationary observer, because they are accelerating. They are straight because there's been some serious deformation of the axes, so this is not a Minkowski ST diagram. Therefore it's not odd that to change frames we use Gallilean transformations. If we plotted the worldlines in a Minkowski diagram, the LT would connect instants on the worldlines.

There are lots of coordinate transformations going on in those notes that are not explicitly stated. But he does say how the conformal coordinates are found

Sometimes it is convenient to "divide out" the expansion of the Universe, and the space-time diagram shows the result of dividing the spatial coordinate by a(t). Now the worldlines of galaxies are all vertical lines.

(my emphasis)

 

[PeterDonis]

This is why I'm saying I get different answers depending on who answers. http://www.astro.ucla.edu/~wright/cosmo_03.htm" "But in cosmological models we do have cosmic time, which is the proper time since the Big Bang measured by comoving observers, and it can be used to set up a deck of cards."

It has to be proper time that he's talking about, because, he then proceeds to do a Galilean Transformation on the diagram. The reason that it's valid to do this transformation is that the horizontal lines in the diagram represent lines of constant PROPER time. (Specifically, proper time for particular observers, who are following particular worldlines.)

While I have no objection to graphing proper time vs. position, this way, I think we deserve a certain amount of clarity about which is being graphed, because it can be either one or the other, but not both.

I agree that some clarification of terms is in order:

(1) The FRW *spacetime* is a geometric object; it can be described using a number of different coordinate systems or charts (or metrics--see next item), but it's the same geometric object no matter what chart/metric is used to describe it. So statements about invariant quantities, like the proper time experienced by a given observer with a given worldline between two events on that worldline (e.g., the big bang and the Earth "now", events O and N in your terminology from an earlier post), are independent of the specific coordinate chart/metric being used.

(2) What I've been calling the Robertson-Walker *metric* is a specific coordinate system used to describe the FRW spacetime, along with the expression for the metric using that coordinate system. (The expression "coordinate chart" is also sometimes used to refer to a coordinate system.) This coordinate system is useful because it has the property I described, that in this particular coordinate system, the "time" coordinate t happens to directly represent the proper time experienced by "comoving observers", observers who remain at the same spatial coordinates (r, theta, phi) for all time. But this is a property of the particular coordinate system; a different coordinate system may not have it (see next item).

(3) What Mentz114 is calling the Painleve chart for the FRW spacetime is a different coordinate system used to describe that spacetime, in which the metric looks quite different than it does in the Robertson-Walker coordinate system. In this coordinate system, the "time" coordinate t does *not* directly represent the proper time of "comoving" observers (at least, I don't think it does based on looking at the metric--Mentz114, please correct me if I'm wrong). But again, this is a property of the specific coordinate system.

(4) Finally, a note on "coordinate time" vs. "proper time". Coordinate time is just what it says: in a coordinate system, there will be one coordinate which is "timelike" and three which are "spacelike" (unless you're using null coordinates, which I won't go into here). The one timelike coordinate is "coordinate time". It's nice if you can set up the coordinate system so the timelike coordinate has at least some kind of actual physical meaning, but there's nothing that requires you to. Proper time, on the other hand, is an invariant quantity, and as I noted above, it must be the same regardless of what coordinate system is used to calculate it. But, as I've also noted, in order to even talk about proper time you have to specify a worldline and events on that worldline (as in the example I gave, the proper time experienced by a "comoving observer" between events O and N).

With the above clarification of terms, hopefully the meaning of what Ned Wright was saying is clearer. Because he explicitly says that he is using the proper time of comoving observers to set up his "deck of cards", I deduce (though he doesn't say so explicitly) that he is using the Robertson-Walker coordinate system. In that coordinate system, the "Galilean transformation" he does is just a spatial translation, moving the origin of the spatial coordinates to a different comoving observer, without changing anything else.

If we have a space vs. proper-time graph, the speed of light should be represented as horizontal lines; not light cones. If we have a space vs TIME graph, then it is not valid to do a galilean transformation, because the relativity of simultaneity has to come into play.

I don't understand either of these statements. What is the difference between a "space vs. proper time" and "space vs. time" graph? In either case, you have the horizontal dimension representing space and the vertical dimension representing time (the only difference is that in the first case, you're specifying that the time coordinate you're using in the vertical dimension directly represents proper time for observers who stay at constant values of all the space coordinates, as with, for example, the Robertson-Walker coordinates as I defined them above). And in either case, light can't possibly travel on horizontal lines, because light doesn't travel in lines of constant time; it travels on null worldlines, and the lines of constant time (the horizontal lines in the diagrams) are spacelike lines. Also, the "Galilean transformation" Ned Wright does leaves the surfaces of constant time invariant; as I noted above, it's just a spatial translation, without changing anything else. Pure spatial translations don't bring in any of the issues involved with relativity of simultaneity. (This is true even in the standard Minkowski coordinates of special relativity; I can always move the spatial origin to a new spatial location without affecting anything else except the specific space coordinates I assign to specific events.)

 

[JDoolin]

I agree that some clarification of terms is in order:

(1) The FRW *spacetime* is a geometric object; it can be described using a number of different coordinate systems or charts (or metrics--see next item), but it's the same geometric object no matter what chart/metric is used to describe it. So statements about invariant quantities, like the proper time experienced by a given observer with a given worldline between two events on that worldline (e.g., the big bang and the Earth "now", events O and N in your terminology from an earlier post), are independent of the specific coordinate chart/metric being used.

2) What I've been calling the Robertson-Walker *metric* is a specific coordinate system used to describe the FRW spacetime, along with the expression for the metric using that coordinate system. (The expression "coordinate chart" is also sometimes used to refer to a coordinate system.) This coordinate system is useful because it has the property I described, that in this particular coordinate system, the "time" coordinate t happens to directly represent the proper time experienced by "comoving observers", observers who remain at the same spatial coordinates (r, theta, phi) for all time. But this is a property of the particular coordinate system; a different coordinate system may not have it (see next item).

(3) What Mentz114 is calling the Painleve chart for the FRW spacetime is a different coordinate system used to describe that spacetime, in which the metric looks quite different than it does in the Robertson-Walker coordinate system. In this coordinate system, the "time" coordinate t does *not* directly represent the proper time of "comoving" observers (at least, I don't think it does based on looking at the metric--Mentz114, please correct me if I'm wrong). But again, this is a property of the specific coordinate system.

(4) Finally, a note on "coordinate time" vs. "proper time". Coordinate time is just what it says: in a coordinate system, there will be one coordinate which is "timelike" and three which are "spacelike" (unless you're using null coordinates, which I won't go into here). The one timelike coordinate is "coordinate time". It's nice if you can set up the coordinate system so the timelike coordinate has at least some kind of actual physical meaning, but there's nothing that requires you to. Proper time, on the other hand, is an invariant quantity, and as I noted above, it must be the same regardless of what coordinate system is used to calculate it.

But, as I've also noted, in order to even talk about proper time you have to specify a worldline and events on that worldline (as in the example I gave, the proper time experienced by a "comoving observer" between events O and N).

Yes, proper time (OF A WORLDLINE) is an invariant quantity, but proper time is NOT A COORDINATE. Coordinates are contravariant; not invariant. Proper time is a property of a worldline. By itself, proper time does not tell you when the event occurs, unless you also know the world-line-path that the particle has followed.

A good coordinate time will tell you when the event occurred, even if you don't know the world-line-path taken to arrive at that event.

With the above clarification of terms, hopefully the meaning of what Ned Wright was saying is clearer. Because he explicitly says that he is using the proper time of comoving observers to set up his "deck of cards", I deduce (though he doesn't say so explicitly) that he is using the Robertson-Walker coordinate system. In that coordinate system, the "Galilean transformation" he does is just a spatial translation, moving the origin of the spatial coordinates to a different comoving observer, without changing anything else.



I don't understand either of these statements. What is the difference between a "space vs. proper time" and "space vs. time" graph? In either case, you have the horizontal dimension representing space and the vertical dimension representing time (the only difference is that in the first case, you're specifying that the time coordinate you're using in the vertical dimension directly represents proper time for observers who stay at constant values of all the space coordinates, as with, for example, the Robertson-Walker coordinates as I defined them above). And in either case, light can't possibly travel on horizontal lines, because light doesn't travel in lines of constant time; it travels on null worldlines, and the lines of constant time (the horizontal lines in the diagrams) are spacelike lines. Also, the "Galilean transformation" Ned Wright does leaves the surfaces of constant time invariant; as I noted above, it's just a spatial translation, without changing anything else. Pure spatial translations don't bring in any of the issues involved with relativity of simultaneity. (This is true even in the standard Minkowski coordinates of special relativity; I can always move the spatial origin to a new spatial location without affecting anything else except the specific space coordinates I assign to specific events.)

In Minkowski Spacetime, a spatial translation is done by taking the paper your graph is drawn on, and moving it, to the left or right. A velocity change is done by Lorentz Transformation.

But in Friedmann-Walker, (Let me see if I've got this right) a pure spatial translation is represented by a Galilean Transformation, and an actual velocity change is simply beyond the scope of General Relativity.

What makes up a geometric object? Are you sure you can graph an invariant vs. a contravariant quantity, and that qualifies as a geometric object? It seems to me that the thing that Robertson Walker did was just set the contravariant coordinate-time equal to the invariant proper time of a bunch of particles that don't even exist, except by statistical average.

I'd like to know why; what was their point? What made this necessary?

I'd also like to know whether, once you set your coordinate time and proper time equal, is it even possible to determine the effect of a large acceleration?

And if I take$$\tau=t$$ and plug it into $$d\tau^2=dt^2-dx^2$$ I get dx=0, suggesting that nothing can ever change its position. (correction: This is to be expected since the \tau represents properties of particles for whom dx is equal to zero. However, I still think that saying \tau is "timelike" is an overgeneralization. \tau and t are really quantities of a fundamentally different sort.)

 

[PeterDonis]

Yes, proper time (OF A WORLDLINE) is an invariant quantity, but proper time is NOT A COORDINATE. Coordinates are contravariant; not invariant. Proper time is a property of a worldline. By itself, proper time does not tell you when the event occurs, unless you also know the world-line-path that the particle has followed.

I think some more clarification of terminology is in order; I should have clarified this before since we've been using the term "proper time" in more than one sense.

(1) Proper time *along a particular worldline between two particular events* is an invariant; geometrically, it's the analogue in spacetime of the invariant "length" of a particular line segment in a Euclidean space.

(2) Proper time *along a particular worldline*, without specifying events on the worldline, is a *parameter*: a range of real numbers you can use to label events on the worldline, by arbitrarily assigning some particular event the value 0 and then labeling every other event by its invariant proper time along the worldline from the event with the value 0 (with earlier events having negative proper time and later events having positive proper time).

(3) Once you have a labeling of events on a worldline by the proper time parameter, you can then look for a coordinate system that uses that same event labeling as its time coordinate. If you're really lucky, you can find a coordinate system that does this, not just for one worldline, but for a whole family of worldlines that are picked out by some symmetry property of the spacetime. This is what is meant by "coordinate time directly represents proper time" for a particular family of observers (in the case I've been discussing, the "comoving" observers).

(Actually, technically *any* definition of a coordinate system with a time coordinate implicitly specifies a "family of observers", in a sense I'll define below; but that family may not make much sense physically, depending on how the coordinate system is defined. See next comment.)

A good coordinate time will tell you when the event occurred, even if you don't know the world-line-path taken to arrive at that event.

But when the event occurred is frame-dependent (i.e., coordinate system dependent); it's not an invariant. That means that specifying when an event occurs requires specifying a coordinate system; and specifying a coordinate system requires specifying a time coordinate; and specifying a time coordinate implicitly specifies a family of worldlines, the integral curves of the vector field defined by that time coordinate (more precisely, defined by the partial derivative operator with respect to that time coordinate).

Depending on the particular coordinate system, this family of curves may or may not make much sense physically, interpreted as the worldlines of a family of observers; but in spacetimes with particular symmetries, those symmetries will pick out certain families of curves, and therefore certain coordinate systems that have those curves as the integral curves of their time coordinates; and those curves will (at least in the cases we're discussing) make sense as the worldlines of a family of observers. The time coordinate of the coordinate system then directly represents the proper time of those observers, in the sense I described above; and therefore specifying when events occur according to this time coordinate *is* specifying the proper time of those events with reference to that family of observers, without having to know the specific worldline path taken to arrive at the event.

In all these cases, though, when events occur is still frame-dependent, and as I think I've said before, I think it's a mistake to insist on thinking about relativistic physics in terms of frame-dependent quantities. Coordinate systems can be a calculational convenience, but they are not *necessary* for doing physics; you can write all the actual physics, if necessary, solely in terms of invariant quantities, without ever specifying a coordinate system.

In Minkowski Spacetime, a spatial translation is done by taking the paper your graph is drawn on, and moving it, to the left or right. A velocity change is done by Lorentz Transformation.

But in Friedmann-Walker, (Let me see if I've got this right) a pure spatial translation is represented by a Galilean Transformation, and an actual velocity change is simply beyond the scope of General Relativity.

You could do a "velocity change" in the FRW spacetime, but the resulting coordinate system would no longer respect the symmetries of the spacetime--the metric would look different (because space would no longer look isotropic in the "moving" frame--Earth itself is an example of such a "moving frame", since the CMBR does not look isotropic to us). That makes it a different case from Minkowski spacetime, where a Lorentz transformation leaves the metric looking the same in the transformed coordinates as it does in the original coordinates.

What makes up a geometric object? Are you sure you can graph an invariant vs. a contravariant quantity, and that qualifies as a geometric object? It seems to me that the thing that Robertson Walker did was just set the contravariant coordinate-time equal to the invariant proper time of a bunch of particles that don't even exist, except by statistical average.

I'd like to know why; what was their point? What made this necessary?

The FRW metric is determined by the condition that the universe is homogeneous and isotropic (it looks the same everywhere and in all directions). We know this condition isn't exactly fulfilled by our universe, but it's close, and the condition makes the mathematics tractable for expressing solutions in closed form. More detailed models take the FRW solution as a starting point and do an expansion about it in powers of small perturbations from exact isotropy, which gives more precise answers but requires numerical solutions.

The existence of a family of observers whose proper time is directly represented by the time coordinate in the FRW metric is something that *appears* in the solution, not something that is put in at the start. Basically, it amounts to looking at the integral curves of the FRW time coordinate, as I described above.

I still think that saying \tau is "timelike" is an overgeneralization. \tau and t are really quantities of a fundamentally different sort.)

As you note in your correction, saying that coordinate time directly represents proper time is not the same as setting tau equal to t in the metric to begin with; you first impose a condition on the metric (such as your dx = 0, which I stated in an earlier post as dr = dtheta = dphi = 0), and then see what the metric looks like with the condition imposed. But that also means that even though tau and t *are* different kinds of quantities, there can still be a relationship between them under certain conditions. For example, we impose the condition that all the space coordinates are constant on the FRW metric and obtain $d\tau^{2} = dt^{2}$. Since there are no other coefficients on either side, that means that tau and t must be measured in the same units, so it makes sense to talk about t "representing" tau for the particular family of observers that meets the condition we imposed. Also, since the signs are the same on both sides, tau must represent a timelike interval (positive squared length, using the sign convention I've been using), so it makes sense to call tau "timelike". (And in fact, this latter property holds in general: for *any* observer moving on a timelike worldline, tau along that worldline will have a positive square.)

 

[PeterDonis]

What makes up a geometric object? Are you sure you can graph an invariant vs. a contravariant quantity, and that qualifies as a geometric object?

I realized on reading over my last post that I didn't fully respond to this point. A geometric object is, by definition, invariant; the object itself remains the same regardless of what coordinate system you use to label points in it. You don't "make" a geometric object by graphing anything; you draw graphs to illustrate how a particular coordinate system represents points, curves, etc. in a geometric object (or a portion of one). What you graph are always coordinates, but sometimes, as I noted in my last post, a particular coordinate happens to represent something with direct physical meaning, such as coordinate time representing proper time (in the sense I described in my last post).