Conductivity and Electric Field relationship

[arhzz]

Homework Statement

a)How large must the conductivity values γ1 and γ2 be chosen if at
a current density J = 2.5 · 10−2 A / cm2
in the layer (1) the power P1 =
600W and in layer (2) the power P2 = 400W should be implemented?
b)Calculate the ratio of the field strengths E1 / E2.
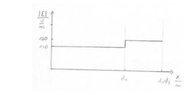
c) Sketch it as function of x
d) Where are the charges gathering

Relevant Equations

-

Okay so this is how it looks like,and there are the given values;

a) I've tried it like this. So I now this formula $$ E = \frac{J}{\sigma} $$ where sigma is the conductivity value. Now to get E we need this formula;

$$ U = \int_{l}{} E \ ds ] $$ Now to get U we can use the $U = \frac{P}{I}$ and to get I we can use this formula

$$ J = \frac{I}{A} $$ simply rearange and we gat that I should be 50 A. Than I calcualted U1 and U2, should be 12 and 8V respectivly. Now to get U I have derived both sides to get rid of the integral and get this formula

$$ E = \frac{dU}{ds} $$ . where s is the length. Now I am not sure If I did this correctly,but since we need the dU and dS but the voltage and length is not changing I just input the values I have E1 = 120 V/m and E2 = 160 V/m. Plug that into the formula for sigma and we get

$\sigma_1 = 2,08 S/m$ and ## \sigma_2 = 1,56 S/m. Now this is according to my solution sheet correct but what is bothering me is I am not sure I can calculate E just like that. Is it okay to assume that the values of U and s are not changing and just plug them in? If not than I'd have to use their derivations,but since they are constants that would be just 0?

b) This is the part that is giving me the most problems,since I don't undestand it.The solution is this $$ \frac{E1}{E2} = \frac{\sigma_2}{\sigma_1} $$ I am not really sure what they want to show me here,any hint on how to start this would be great.c) I did it like this(see picture in attachemnet) I think that should be fine,I am not really sure how to do it otherwise;

d) Now i'd say the places are x = 0, x =d1 and x=d1+d2; The reason being that in order to generate the electric field the charges need to move,and since we have an electric field in both of the layers,the charges are on the "edges" of each layer.Not sure if the explanation is on point but that would be my go to.

Any help on the part b) would be great.

Thanks and excuse the long post!

 

[kuruman]

In part (b) they want you to find the ratio of the electric fields in each medium. Hint: To get that ratio, you need to consider that what you have here is resistors in series, therefore $\dots$

For part (d) I think you could say more if you use Gauss's law.

 

[arhzz]

In part (b) they want you to find the ratio of the electric fields in each medium. Hint: To get that ratio, you need to consider that what you have here is resistors in series, therefore $\dots$

For part (d) I think you could say more if you use Gauss's law.

Okay for part d, I will look into it,great advice.

For part b I don't think I fully understand.Where are the resistors? Are (1) and (2) the resistors.Now if they are resistors would the Ohms Law be useful here? Or should I look on the relationship between electric fields and resistors?

 

[kuruman]

For part b I don't think I fully understand.Where are the resistors? Are (1) and (2) the resistors.Now if they are resistors would the Ohms Law be useful here? Or should I look on the relationship between electric fields and resistors?

Conductivity is the inverse of resistivity. It is logical to deduce then that something that has non-zero conductivity must have non-zero resistivity. So $J=\sigma~ E \rightarrow E=\rho~J.$ The latter form is also known as Ohm's law. For conductors of uniform cross-section $A$ (as we have here), with $J=I A$ and $E= V/l$ one gets $$E=\rho~J \rightarrow \frac{V}{l}=\rho\frac{I}{A} \implies V=IR~~~~\left(R\equiv\frac{\rho A}{l}\right).$$Have you not seen this before? Here, in the steady-state, whatever current (charge per unit time) flows through the resistor on the left must flow through the resistor on the right. With that realization part (b) is trivial.

 

[arhzz]

Conductivity is the inverse of resistivity. It is logical to deduce then that something that has non-zero conductivity must have non-zero resistivity. So $J=\sigma~ E \rightarrow E=\rho~J.$ The latter form is also known as Ohm's law. For conductors of uniform cross-section $A$ (as we have here), with $J=I A$ and $E= V/l$ one gets $$E=\rho~J \rightarrow \frac{V}{l}=\rho\frac{I}{A} \implies V=IR~~~~\left(R\equiv\frac{\rho A}{l}\right).$$Have you not seen this before? Here, in the steady-state, whatever current (charge per unit time) flows through the resistor on the left must flow through the resistor on the right. With that realization part (b) is trivial.

Yea actually I have seen this before but it honestly did not occur to me. I am going to assume that ur V is how you designate Voltage (not U like in Europe). I think I get it now,I will try to solve it in the morning; I'll let you know how it goes.

 

[kuruman]

Yea actually I have seen this before but it honestly did not occur to me. I am going to assume that ur V is how you designate Voltage (not U like in Europe). I think I get it now,I will try to solve it in the morning; I'll let you know how it goes.

Yes, $V$ is voltage.

 

[arhzz]

Okay so this is my final answer.So we know that the formula is $J = \sigma E$.Now that the J in both resistors (or layers of medium) is the same we can say that J1 = J2; hence

$$\sigma_1E1 = \sigma_2E2 $$ and from that we can already get to the wanted ratio.

Also for part d) I've read through the Gauss law; Although a bit complicated and advanced I was able to get the answer I wanted.

Thanks for the help!