Conventional absorbtion spectra and E_g

[prehisto]

Hi,
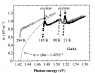
I have measured conventional absorption spectra of semiconductor - Optical density from wavelenght.
So now I want to evaluate band gap for this material.

In what kind of coordinates I how to reperesnt this spectra to see the band gap value ( where graph crosses the Energy axis) ?

*I m investigating semicondcutor

 

[mcodesmart]

The band gap is the minimum photon energy where you can see the absorption. it is characterized by a threshold behavior. The aborption below the bandgap should be zero (at least for direct band gap semiconductors, (ALSO PLEASE NOTE Franz-Keldysh Effect).

The absorption above the band gap is characterized by a (hw - E_g)^1/2 behavior.

 

[Cthugha]

The absorption above the band gap is characterized by a (hw - E_g)^1/2 behavior.

...for a bulk (3D) material.

For a semiconductor one might also see a pronounced resonance feature slightly below the band gap energy due to absorption by excitons (bound electron-hole pairs).

The easiest thing is to simply plot absorption versus photon energy. The band gap should become pretty obvious from that graph.

 

[mcodesmart]

Attached is the experimental data for GaAs. Please take a look and I would be interested in your comments.

I think that exciton absorption that you mentioned are occurring above the band gap energy. You can also see the threshold behavior that I mentioned.

 

[Cthugha]

An exciton is a hydrogen-like bound state of an electron and a hole. Its lowest possible energy is therefore the smallest possible energy of a free electron and a free hole (which is the band gap) minus the binding energy. However, this binding energy may be quite small (for 3D GaAs we are talking about roughly 4.8 meV only) and the exciton also has some dispersion which means that it also can have some kinetic energy which slightly broadens the excitonic absorption.

It is hard to see for materials with small exciton binding energy, but excitonic (ground state) absorption must be below the band gap. This might be easier to see when fitting a superposition of the free carrier absorption and the excitonic absorption. It might be easier to see for materials with larger exciton binding energy like Cu2O or maybe ZnO or some II-VI semiconductors. It might also be easier to see for quantum wells, where the dimensionality enhances the binding energy and modifies the density of states and accordingly the shape of the free carrier absorption.

 

[prehisto]

Thank you all for your help.

The absorption above the band gap is characterized by a (hw - E_g)^1/2 behavior.

I think the best way is to calculate absorption by \alpha=a (hw - E_g)^1/2, but i have several samples withdifferent linear sizes.
So I am thinking that linear size should have impact to \alpha.
And i don't know how to calculate "a" because it has many variables,which could be dependent from specific semiconductor.

Perhaps I can assume some kind of value for "a'"? But in that case how can I consider the impact of linear size of different samples?

 

[Cthugha]

So I am thinking that linear size should have impact to \alpha.

Not really. It gives you a rather irrelevant factor, but it does not change the shape of every single absorption curve which is the important thing in determining the band gap.

For the same reason I do not see why one would want to calculate a. You plot your absorption vs. wavelength, fit the relevant equation to it and see whether the result makes sense or you should rather use a different function for fitting. There is no deep physical insight about the band gap you get by knowing a.

Here, I assume that your measurement goes as follows: you check the relative absorption of your sample at some wavelength, change your optical wavelength, measure absorption again, change wavelength again and so on.

 

[prehisto]

OK,I understand now that i do not need " a".
But now i have a problem,becuase i need to calculate \alpha from optical density.
And again i do not know how to do that, could someone can help ?

 

[mcodesmart]

O.D measurements depend on sample length.

10^{-OD} = I(z)/I_o

replace I(z) with I_o e^{-αl} and work it out..

The answer is OD = 0.434 αl

 

[Cthugha]

OK,I understand now that i do not need " a".
But now i have a problem,becuase i need to calculate \alpha from optical density.
And again i do not know how to do that, could someone can help ?

As mcodesmart already explained, this will fortunately just be a simple prefactor to your OD. Unless you already have different linear sizes for different wavelenghts within one single run of the experiment, the shape of the OD curve and the absorption curve (which is what matters in determining the band gap) will be the same for each single linear size (assuming you measured the OD for all wavelengths for a given linear size and then did the same for the next size and so on).

 

[prehisto]

I measured the OD for all wavelengths for a given linear size.
Then i plotted \alpha² from energy(eV).

So now I can determine the E_g where trendline crosses Energy axis (\alpha=0) .

But it looks not so great as i expected because of defects levels in bandgap .

 

[mcodesmart]

You mind sharing your results so we can take a look as well.. I am curious and also, what material is it..