Amaelle
- 309
- 54
- Homework Statement
- look at the image
- Relevant Equations
- Set of convergence
Greetings
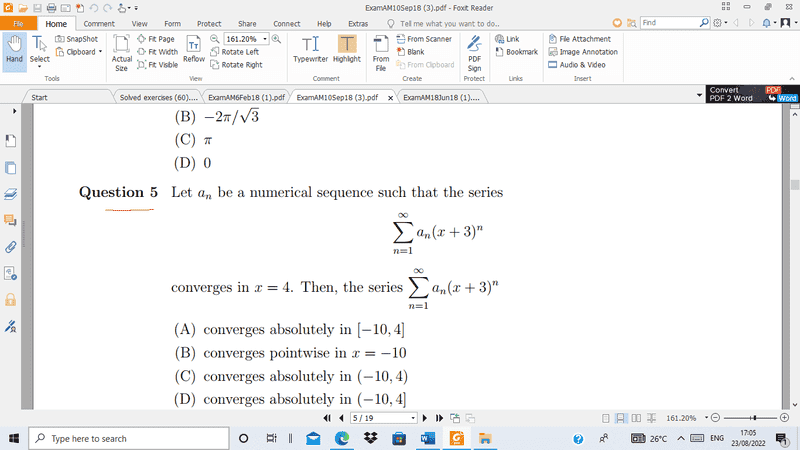
According to my understanding: if x converges in 4 means that the series converges -1<x+3<7 but the solution says C
Any hint?
thank you!
According to my understanding: if x converges in 4 means that the series converges -1<x+3<7 but the solution says C
Any hint?
thank you!