Cross section (?) of Great Pyramid from drone footage

[neilparker62]

Perhaps we just need to believe what the casing stones are telling us after all!

https://arkysite.wordpress.com/2013...e-of-giza-at-the-national-museum-of-scotland/

In summary $\cot^{-1}{(\frac{5}{7} + \frac{2}{28})}=\tan^{-1} \frac{14}{11}=51.84^{\circ}.$

Worth noting that $\frac{11}{14}=\frac{1}{4} \times \frac{22}{7} \approx \frac{\pi}{4}$

In Egyptian measurements, the base length is 440 cubits and the height 280 cubits. Hence:

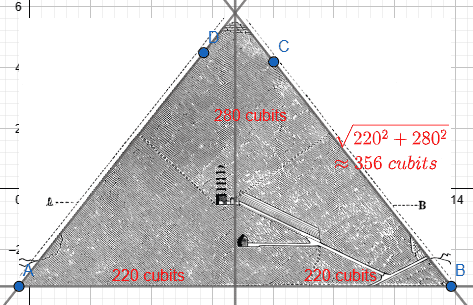
And it just so happens that 220 and 356 are 2 consecutive Fibonacci numbers giving rise to the Kepler / golden ratio triangle theory. $\frac{356}{220} \approx 1.618.$

All the same an accurate measurement of the slope angle - if possible - would still be useful in establishing the tolerances to which the builders worked if we take it as read that the 'design slope' was indeed a rise:run of 14:11.

 

[pbuk]

And it just so happens that 220 and 356 are 2 consecutive Fibonacci numbers giving rise to the Kepler / golden ratio triangle theory. $\frac{356}{220} \approx 1.618.$

Be very careful: there is a great deal of non-science and numerology concerning the Great Pyramids.

We also have $2 \frac {440} {280} \approx \pi$, and note that $\frac {5 - 1} {\sqrt \varphi} \approx \pi \approx \left (1 + \frac 1 5 \right ) \varphi ^ 2$: which number has the most magic: $\varphi, \pi$, 5 or 1?

 

[neilparker62]

Be very careful: there is a great deal of non-science and numerology concerning the Great Pyramids.

We also have $2 \frac {440} {280} \approx \pi$, and note that $\frac {5 - 1} {\sqrt \varphi} \approx \pi \approx \left (1 + \frac 1 5 \right ) \varphi ^ 2$: which number has the most magic: $\varphi, \pi$, 5 or 1?

Agreed. I hope that making it clear where the "numerology" comes from debunks it to some extent. Whilst not discounting the possibility that the Ancient Egyptians might have had a more nuanced understanding of numbers than simple numeric ratios.

 

[neilparker62]

Maybe the idea needs a re-think! Here is my drone pic super-imposed upon a surveyed cross-sectional view.

 

[Devin-M]

I can't remember where I read it from but somewhere I learned on the internet that the cross section and alignment of the interior passageways of the great pyramid is based on the heptagram (7 pointed star). I made this diagram to illustrate...

 

[neilparker62]

As has been cautioned in an earlier post , we are not dealing in numerology here.

 

[Devin-M]

I'm just talking about the angle of the outer walls, the location of the entrance, the slope of the entrance passageway, the slope of the ascending passageway and the "aim points" of the "air shafts," and the location of the "subterranean chamber."

 

[neilparker62]

Interesting geometry certainly. Your regular heptagon produces a slope angle of $51.43^{\circ}$ which is not far off the $51.86^{\circ}$ indicated by Flinders Petrie. I am a little puzzled by where the two air shafts join - is that supposed to be the centre of the heptagon ? Concerning location of the entrance. Again not a bad fit with one side of your regular heptagon showing a slope of $25.71^{\circ}$ as compared to the $26.45^{\circ}$ supplied again by Flinders Petrie.

 

[Devin-M]

It's also interesting to note (from my own observation) that the King's Chamber and Subterranean Chamber appear equidistant from the intersection of the ascending chamber and descending chamber... so in other words if you flip this diagram upside-down along the axis joining that intersection with the same "virtual" intersection on the opposite side, the King's Chamber would be at the same position as the subterranean chamber, the point formed by the corner of this heptagram that follows the line formed by the ascending passage is at ground level...

 

[DaveC426913]

Having grown up with von Daniken (Chariots of the Gods) and his ilk, I'm quite dubious about conjectures that provide their own "data" and then provide their own astonishing conclusions from that "data". ("Data" being a generous word for a low-rez diagram.)

In the above diagram, how do we know:
1. that the unsullied diagrams of the pyramid's geometry is accurate?
2. that the geometry laid overtop is accurate to within sufficient error margins as to be inarguable?

For all we know, this the diagrammatic equivalent of a self-fulfilling prophecy.

Without the original data, this is not science or math. It's numerology.

 

[Devin-M]

In the above diagram, how do we know:
1. that the unsullied diagrams of the pyramid's geometry is accurate?
2. that the geometry laid overtop is accurate to within sufficient error margins as to be inarguable?

Sorry about that! Redrawn with pyramid diagram and heptagram overlaid diagram both from wikipedia:

 

[berkeman]

Thread closed for Moderation...

 

[jim mcnamara]

Thread closed.