mathmari
Gold Member
MHB
- 4,984
- 7
Hey! 
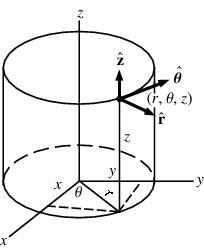
Using cylindrical coordinates and the orthonormal system of vectors $\overrightarrow{e}_r, \overrightarrow{e}_{\theta}, \overrightarrow{e}_z$
Could you give me some hints how I could do that?? (Wondering)
Using cylindrical coordinates and the orthonormal system of vectors $\overrightarrow{e}_r, \overrightarrow{e}_{\theta}, \overrightarrow{e}_z$
- describe each of the $\overrightarrow{e}_r$, $\overrightarrow{e}_{\theta}$ and $\overrightarrow{e}_z$ as a function of $\overrightarrow{i}, \overrightarrow{j}, \overrightarrow{k}$ and $(x, y, z)$ and
- calculate $\overrightarrow{e}_{\theta} \times \overrightarrow{j}$ with two ways: analytically, using (1), and geometrically.
Could you give me some hints how I could do that?? (Wondering)