Determine the Lagrangian for the particle moving in this 3-D cos^2 well

[Lambda96]

Homework Statement

See Screenshot

Relevant Equations

none

Hi,

I am not quite sure whether I have solved the following problem correctly:

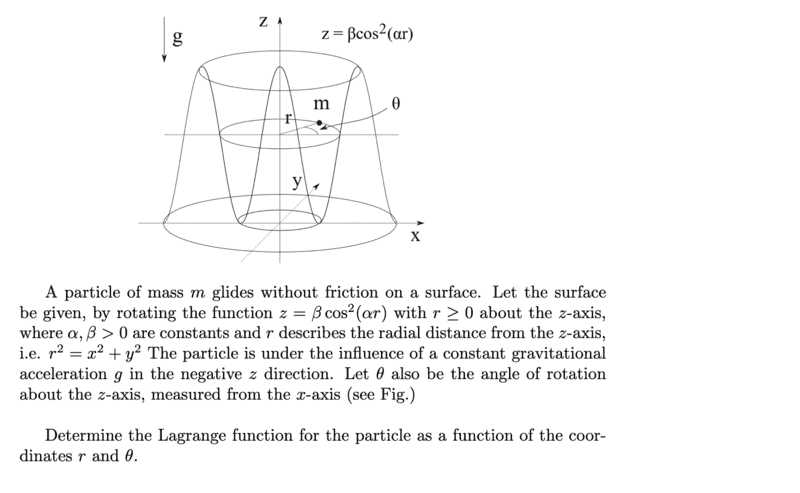
I have now set up Lagrangian in general, i.e.

$$L=T-V=\frac{1}{2}m(\dot{x}^2+\dot{y}^2)-mgz$$

After that I imagined how $x$,$y$ and $z$ must look like and got the following:

$$x=\beta \cos^2(\alpha r) \cos(\theta)$$
$$y=\beta \cos^2(\alpha r) \sin(\theta)$$
$$z=\beta \cos^2(\alpha r)$$Then I determined $\dot{x}$ and $\dot{y}$ or rather $\dot{x}^2$ and $\dot{x}^2$.

$$\dot{x}=-\dot{\theta} \beta \cos^2(\alpha r) \sin(\theta) , \quad \dot{x}^2=\dot{\theta}^2 \beta^2 \cos^4(\alpha r) \sin^2(\theta)$$
$$\dot{y}=\dot{\theta} \beta \cos^2(\alpha r) \cos(\theta) , \quad \dot{y}^2=\dot{\theta}^2 \beta^2 \cos^4(\alpha r) \cos^2(\theta)$$

Then I put everything into the Lagrangian

$$L=\frac{1}{2}m\Bigl[ \dot{\theta}^2 \beta^2 \cos^4(\alpha r) \sin^2(\theta) +\dot{\theta}^2 \beta^2 \cos^4(\alpha r) \cos^2(\theta) \Bigr]-mg\beta \cos^2(\alpha r)$$

$$L=\frac{1}{2}m\dot{\theta}^2 \beta^2 \cos^4(\alpha r)-mg\beta \cos^2(\alpha r)$$

Unfortunately, however, my Lagrangian now depends on $r$ and $\dot{theta}$ and not $r$ and $\theta$.

 

[vanhees71]

I don't understand, how you came to your equations for $x$ and $y$. Think again about, how to parametrize $(x,y,z)$ as a function of the better adapted generalized independent variables $r$ and $\theta$!

 

[PhDeezNutz]

First you are definitely missing a $\dot{z}^2$ term in your Kinetic Energy.

Now think cylindrical coordinates.

Isn't $r = \sqrt{x^2 + y^2}$?

What are $x$ and $y$ in cylindrical coordinates?

Also I think you interpreted the last sentence wrong

"Determine the Lagrangian in terms of $r$ and $\theta$" to me does not imply that $\dot{r}$ and $\dot{\theta}$ can't be present.

 

[PhDeezNutz]

$$x=\beta \cos^2(\alpha r) \cos(\theta)$$

$$\dot{x}=-\dot{\theta} \beta \cos^2(\alpha r) \sin(\theta) $$

Even if $x$ were computed correctly. Computing $\dot{x}$ requires not just the chain rule but the product rule as well. Same goes for $y$.

Your coordinates are both $r$ and $\theta$. Take that into account.

 

[Lambda96]

Thank you vanhees71 and PhDeezNutz for your help.

Unfortunately I completely misunderstood the task, I thought that the particle m would stay on this circular path, but the particle is supposed to move completely over the surface of this, I'll call it funnel, so $r$ does not stay constant, but depends on time.

For the z coordinate I can use the formula given, i.e. $z=\beta \cos(\alpha r)^2$ for the $x$ and $y$ I would use polar coordinates, as PhDeezNutz has already pointed out. So I would get the following for the $x, y, z$ and their time derivatives

$$x=r \cos(\theta) , \qquad \dot{x}=\dot{r} \cos(\theta)-r \dot{\theta} \sin{\theta} , \qquad \dot{x}^2=\dot{r}^2 \cos^2(\theta)-2 \dot{r} r \dot{\theta} \sin(\theta) \cos(\theta)+r^2 \dot{\theta}^2 \sin^2{\theta}$$
$$y=r \sin(\theta) , \qquad \dot{y}=\dot{r} \sin(\theta)+r \dot{\theta} \cos{\theta} , \qquad \dot{y}^2=\dot{r}^2 \sin^2(\theta)+2 \dot{r} r \dot{\theta} \cos(\theta) \sin(\theta)+r^2 \dot{\theta}^2 \cos^2{\theta}$$
$$z= \beta \cos^2(\alpha r) , \qquad \dot{z}=-2 \beta \alpha \dot{r} \sin(\alpha r) \cos(\alpha r), \qquad \dot{z}=4 \beta^2 \alpha^2 \dot{r}^2 \sin^2(\alpha r) \cos(\alpha r)^2$$

I then substituted these values into the Lagrangian and got the following:

$$L= \frac{1}{2}m \Bigl\lbrack \dot{r}^2 + r^2 \dot{\theta}^2+4 \beta^2 \alpha^2 \dot{r}^2 \sin^2(\alpha r) \cos^2(\alpha r) \Bigr\rbrack -mg \beta \cos^2(\alpha r)$$

Then I used the following identity for $\dot{z}^2$ $\sin^2(x) \cos^2(x)=\frac{1}{4} \sin^2(2x)$ and get the following form:

$$L= \frac{1}{2}m \Bigl\lbrack \dot{r}^2 + r^2 \dot{\theta}^2+ \beta^2 \alpha^2 \dot{r}^2 \sin^2(2 \alpha r) \Bigr\rbrack -mg \beta \cos^2(\alpha r)$$

 

[PhDeezNutz]

Looks good to me.

 

[Lambda96]

Thank you all for your help