Samuel Williams
- 19
- 3
Hi all, the question is as follows:
1. Homework Statement
From the energy level diagram for OH in the study guide, it can be seen that the first rotationally
excited level of OH (2∏3=2 J =5\2) lies 120 K above the groundstate. What is the wavelength of radiation associated with a transition between the groundstate and the first excited level?
This is an energy level diagram that contains the relevant wavelengths, the numbers in blue are the transition wavelengths, which is what I require.

I would just like to know how to actually calculate the wavelengths.
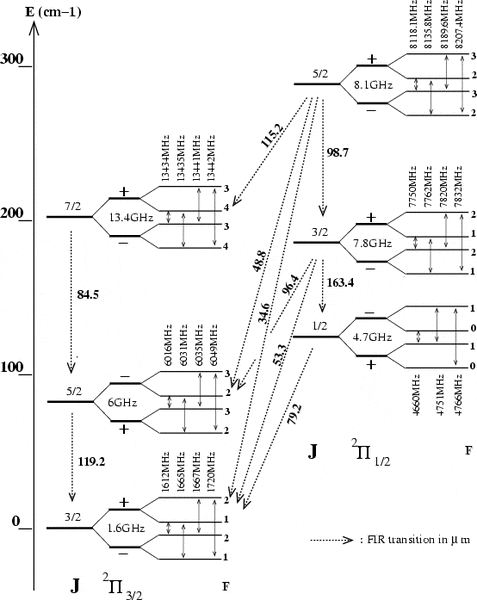
The difference in frequencies is, for example from J = 5/2 to J = 3/2, 4365MHz where the main line frequencies of 1665MHz and 6030MHz are used. However, this corresponds to a wavelength of 0.068m, which is far off of the 0.000119m actual value. I suspect that I am calculating it incorrectly, I am unsure how to actually do it.
1. Homework Statement
From the energy level diagram for OH in the study guide, it can be seen that the first rotationally
excited level of OH (2∏3=2 J =5\2) lies 120 K above the groundstate. What is the wavelength of radiation associated with a transition between the groundstate and the first excited level?
Homework Equations
This is an energy level diagram that contains the relevant wavelengths, the numbers in blue are the transition wavelengths, which is what I require.
I would just like to know how to actually calculate the wavelengths.
The Attempt at a Solution
The difference in frequencies is, for example from J = 5/2 to J = 3/2, 4365MHz where the main line frequencies of 1665MHz and 6030MHz are used. However, this corresponds to a wavelength of 0.068m, which is far off of the 0.000119m actual value. I suspect that I am calculating it incorrectly, I am unsure how to actually do it.

