Developing the Feynman diagram expansion

[ShayanJ]

TL;DR Summary

Trying to figure out Feynman rules from expansion of the generating functional.

I'm reading "introduction to many body physics" by Piers Coleman. In section 7.2 he's trying to introduce Feynman diagrams by expanding the generating functional. But first he transforms it into this pictorial form:

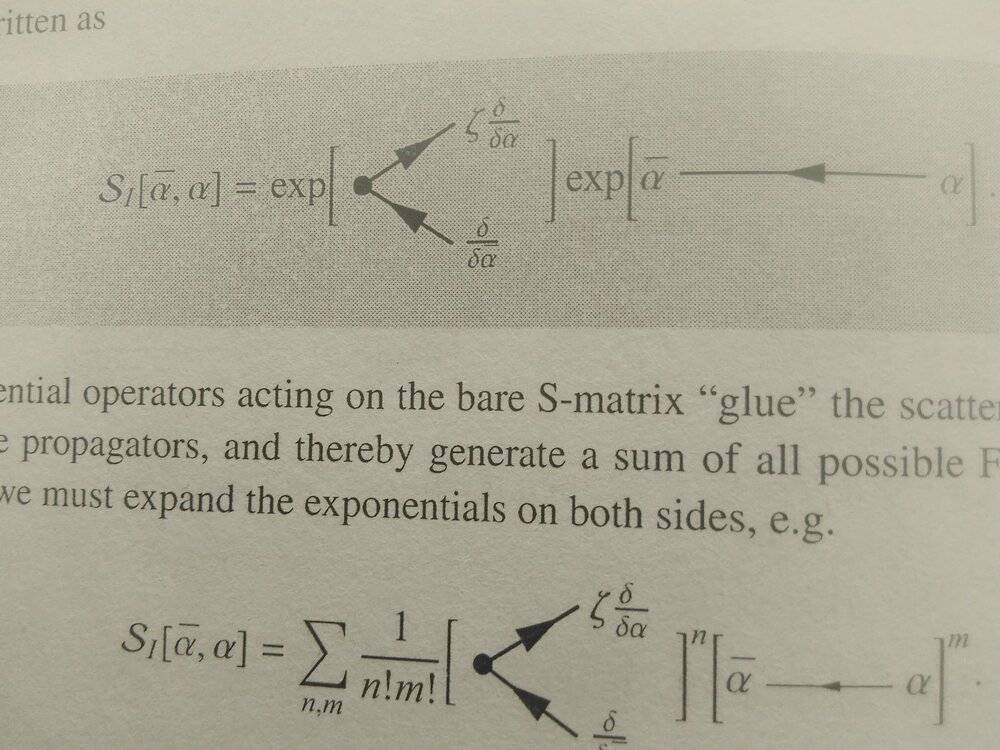
Then he calculates the n=1, m=1 term like below:

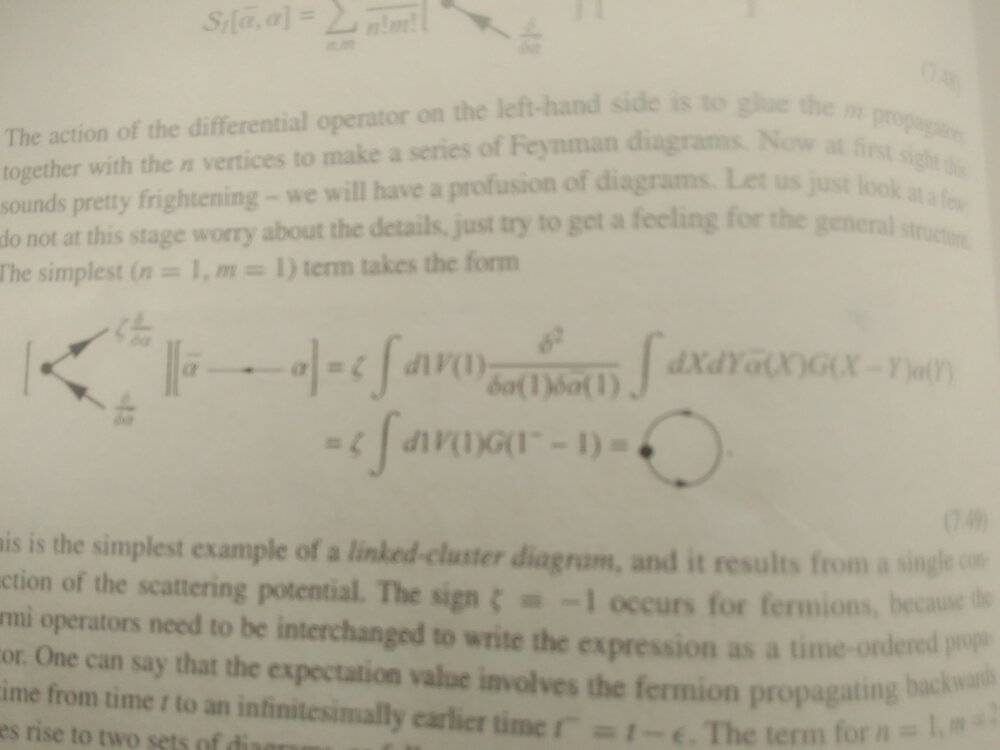
Which I understand. But I have no idea how he calculates the n=1, m=2 term:

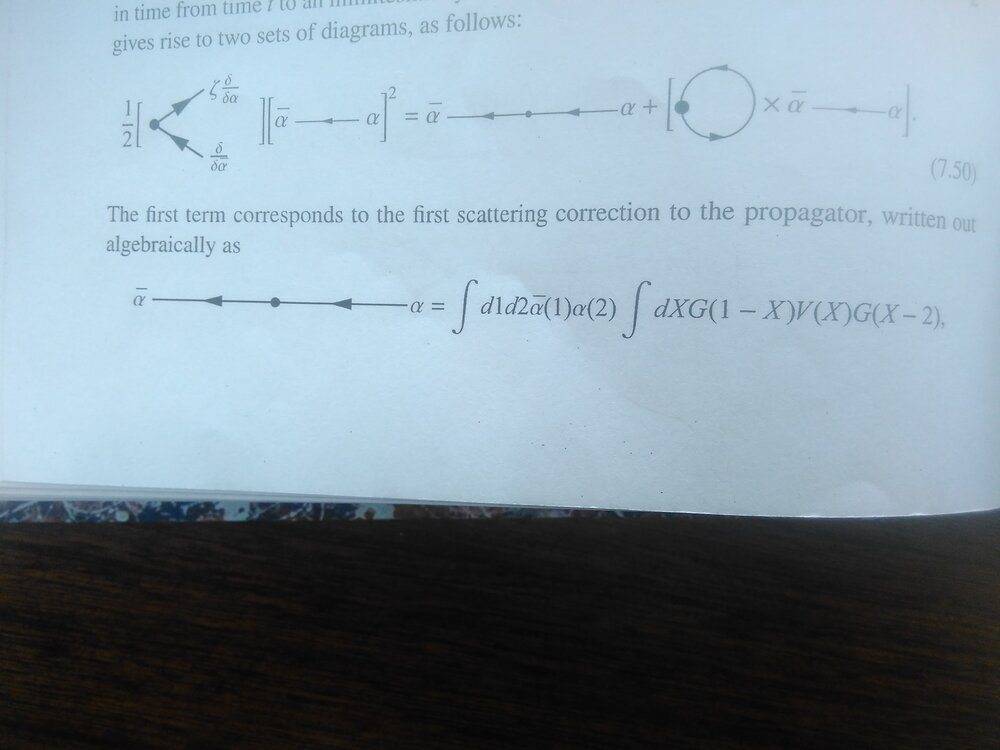
Can anybody help?
Thanks

PS
d1 and 1 mean $dt_1 dx_1$ and $(t_1,x_1)$

 

[ShayanJ]

I figured it out. It was a simple application of the chain rule. I'm really rusty!
$$ \int d1 U(1) \frac{\delta^2}{\delta\alpha \delta\bar \alpha}\left( \int dX dY \bar\alpha(X) G(X-Y) \alpha(Y)\right)^2 = \\ 2 \int d1 U(1) \frac{\delta}{\delta\alpha} \left[\left( \int dX dY \bar\alpha(X) G(X-Y) \alpha(Y)\right) \left( \int dY G(1-Y) \alpha(Y)\right)\right] $$
And so on and so fourth!

 

[Quarkman1]

As Kipling wrote "You're a better man than I, Gunga Din!" I like that you wrote it out and explained what you found. I am extremely rusty. The chain rule is something I need to read up on more, I think it would help me sort of get the grasp of many of the equations, especially with expansions, etc.