Did they do a Loopholes free Bell test?

[Mentz114]

This beautifully crafted experiment now gives rise to a modified Quantum Randi Challenge (for all local realists out there):

I'm not a 'local realist' but I do simulations to test simple hypotheses and this has led me to conclude that the CHSH statistic cannot exceed the limit even with maximally correlated readings. Any simulation which does not include simething extra to mimic the entanglement will not break the limit.

From the 'socks' paper equ(13)

$E(a,b)=P(00|ab)+P(11|ab)-P(01|ab)-P(10|ab)$
$S=E(a,b)+E(a',b)+E(a,b')-E(a',b')$

so if $P(00|ab)+P(11|ab)=0$ (perfect anticorrelation) then $S=-2$.

The (only ?) way to fake entanglement is to transform $E(a,b)$
$E'(a,b)=2\sin(\theta)^2(P(00|ab)+P(11|ab))-2\cos(\theta)^2(P(01|ab)+P(10|ab)$

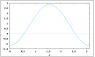
We must identify $\theta$ as a setting on the coincidence gathering apparatus. With this change the value of $S$ for a sample with zero mean correlation, S=2.0 for $\theta=\pi/2$. If the correlation is not zero then S can break the limit. The picture shows S against $\theta$ on the x-axis from a sample that has a correlation of about 0.65 ( this is not a histogram it is $\sin(x)^2$). The sample S value is 2.78 with SD=0.12 ( 100 runs of 1000 samples)

The justification for the cheat comes from the fact that entangling wave equations requires a change of Hilbert space basis ( eg a rotation) from the unentangled bases. The rotation used in the cheat comes from equation (4) in Bells paper.

 

[billschnieder]

With post-selection one usually means selection made after the experiment has been done, using knowledge of the results from both wings of the experiment.

That is precisely the case here. The measurements at Alice and Bob are post-selected after the experiment is done, using the "good" information from C.

Here, the selection is done outside the lightcone of the experiment. There is no way a local hidden variable model could make use of such a selection mechanism in order to violate the CHSH-inequality.

Not relevant to post-selection which is a non-local process irrespective of light-cones.

 

[zonde]

Yes, there is post selection - no quibble about that. But if swapping were not occurring, that sample would not tell us anything. The local realist denies there is swapping that affects the resulting sample. They would say indistinguishability and overlap do not matter. Those things are ingredients for the swapping but NOT for the post-selection. That is what I am saying, as best I can tell.

1. For swapping purposes only. Not for post-selection.

2. HOM is not demonstrated on individual events. Just a couple of clicks separated by a specified timing.

3. As said, it is also post-selection.

4. I don't think so. The clicks in separate detectors show this, correct?

My assertion is that the post-selection steps could be performed WITHOUT indistinguishability (and therefore without swapping). Of course, then the experiment would not work. But the local realist shouldn't care since they will say that nothing that happens at C affects A & B's results. We know that idea is wrong.

First I would like to point out that the idea of entanglement swapping affecting measurement outcomes for entangled particles contradicts realism. Because if swapping happens in future light cones of two other measurements, swapping would have to affect measurements backwards in time.
So it's not about local realism but any realism.

Now let me give my argument why indistinguishability is required for successful post-selection. Here is quote from other paper about previous experiment http://arxiv.org/abs/1212.6136:
"The final state is one of two Bell states $|\psi^\pm \rangle = 1/ \sqrt2 (|\uparrow_A\downarrow_B\rangle \pm |\downarrow_A\uparrow_B\rangle)$, with the sign depending on whether the same detector (+), or different detectors (−) clicked in the two rounds."

Without indistinguishability there would be a phase drift so that instead of two Bell states $|\psi^\pm \rangle = 1/ \sqrt2 (|\uparrow_A\downarrow_B\rangle \pm |\downarrow_A\uparrow_B\rangle)$ we would get one classical state $|\psi \rangle = 1/ \sqrt2 (|\uparrow_A\downarrow_B\rangle \otimes |\downarrow_A\uparrow_B\rangle)$ no matter if the same or different detectors click in the two rounds. And with that classical state we of course can't violate Bell inequalities.

 

[zonde]

Here, the selection is done outside the lightcone of the experiment. There is no way a local hidden variable model could make use of such a selection mechanism in order to violate the CHSH-inequality.

I am not claiming that local hidden variable model can violate the CHSH-inequality using that post-selection.

 

[gill1109]

That is precisely the case here. The measurements at Alice and Bob are post-selected after the experiment is done, using the "good" information from C.

*After* the experiment one has to gather together and correlate the information which has been generated at locations A, B and C. There is nothing wrong with selecting A and B data conditional on what was observed at C if the marker at C saying "go" was set before the randomisation of settings at A and B. See Bell (1981) "Bertlmann's socks", Figure 7 and the discussion of the experimental set-up around figure 7. The crucial point is do you accept that the settings are effectively random? Not available outside of their forward lightcones?

 

[billschnieder]

*After* the experiment one has to gather together and correlate the information which has been generated at locations A, B and C.

Correct. Heinera seems to think otherwise. This experiment is not an "event-ready" experiment, in which Alice and Bob are told "go" each iteration. They measure everything and the results are post-selected *after*.

Post selection introduces nonlocality and nonfactorability in the data.

 

[Heinera]

Correct. Heinera seems to think otherwise. This experiment is not an "event-ready" experiment, in which Alice and Bob are told "go" each iteration. They measure everything and the results are post-selected *after*.

Post selection introduces nonlocality and nonfactorability in the data.

No, I do not think otherwise. The decision to select or not is made before the experiment is performed. If the decision is to not select, what difference does it make if Alice and Bob then perform the experiment or not, when it is already decided that the result will not be used?

 

[billschnieder]

No, I do not think otherwise. The decision to select or not is made before the experiment is performed. If the decision is to not select, what difference does it make if Alice and Bob then perform the experiment or not, when it is already decided that the result will not be used?

Of course the experiment was designed with the intention to select. But the selection is done *after* the experiment not before. Post-selection makes the difference that the resulting *post-selected* ensemble is nonlocal. Alice and Bob do not know at each instant if they should "go" or not. They always do the measurement and only at the *end*, do they reject the "bad" results after the information from C has been communicated to them. That's all I'm saying.

 

[Heinera]

Of course the experiment was designed with the intention to select. But the selection is done *after* the experiment not before.

Post-selection makes the difference that the resulting *post-selected* ensemble is nonlocal. That's all I'm saying.

Then you don't understand the experiment. The decision to select or not is done (and recorded) before each experiment is performed.

 

[gill1109]

Then you don't understand the experiment. The decision to select or not is done (and recorded) before each experiment is performed.

Exactly. The time at which you analyse the data is irrelevant. All CHSH experiments involve bringing data together *after* the experiment and selecting four subsets according to the settings at the two locations. This selection necessarily is done in a non-local way and after the experiment. But so what? The way the data is selected does not bias the estimated correlation. That's the important thing.

 

[billschnieder]

Then you don't understand the experiment. The decision to select or not is done (and recorded) before each experiment is performed.

Perhaps because you are using a very strange meaning of "experiment". The experiment is not just what happens in one iteration. It is certainly a fact that post-selection is done *after* the experiment, which means all the runs have been completed and all the measurements at Alice and Bob have been done. It is also a fact that such post-selection, introduces nonlocality such that the ensemble of results left after filtration is not factorable. This is obvious. This is what I'm saying and I don't think you disagree with that.

The article reports the result of one experiment that involved many iterations. Not 245 separate experiments. Actually, by your definition of "experiment", they did many millions of experiments, and presented the results of just 245 of them. If the "go" signal was available before the "experiment", why waste time to do all the "bad" ones? The reported violation is from jointly considering all 245 "good" results. The fact that there is no non-locality in a single run (which you call "experiment") does not change the fact that as a whole, the final ensemble of "good" results was post-selected and therefore nonlocal.

 

[Heinera]

Perhaps because you are using a very strange meaning of "experiment". The experiment is not just what happens in one iteration.

Yes, with "experiment" I mean what happens in one iteration. Each iteration is an individual experiment.

It is certainly a fact that post-selection is done *after* the experiment, which means all the runs have been completed and all the measurements at Alice and Bob have been done.

This is only for convenience. They could just as well analyze the data in real time, and get an increasingly more significant violation as the experiments progressed. The end result would be the same.

It is also a fact that such post-selection, introduces nonlocality such that the ensemble of results left after filtration is not factorable. This is obvious. This is what I'm saying and I don't think you disagree with that.

No, it's not obvious. In fact, it's wrong, so I do disagree with that.

The article reports the result of one experiment that involved many iterations. Not 245 separate experiments. Actually, by your definition of "experiment", they did many millions of experiments, and presented the results of just 245 of them. If the "go" signal was available before the "experiment", why waste time to do all the "bad" ones?

They were not wasting any time. In order to create the 245 entangled states, they had to make millions of tries. It was those tries that took the time, and they were unavoidable. Whether an experiment was or was not performed after those tries didn't imply any wasting of time (because in order to not perform the experiment, A and B would have to waste time waiting for a return signal from C that said "no-go").

 

[billschnieder]

Yes, with "experiment" I mean what happens in one iteration. Each iteration is an individual experiment.

That's not what I meant by experiment, so you misunderstood what I said.

This is only for convenience. They could just as well analyze the data in real time, and get an increasingly more significant violation as the experiments progressed. The end result would be the same.

Nope they can't, there is no way for Alice (Bob) to know what "experiment" (your definition) is good in real time. Even if there was a way, there is no way to analyze any data in real time. Analysis requires the results from Alice and Bob to be brought together *after* the all the runs have been completed. This is obvious.

No, it's not obvious. In fact, it's wrong, so I do disagree with that.

That is because you don't understand it. It simply is the fact that you need information from both Alice and Bob to filter the results at Alice, as well as the results at Bob. Therefore the filtered results are nonlocal. What is wrong in that? There is no way for Alice to know which of her results are "good" until the information she sends through the photon is compared with the information sent by Bob, and vice versa. it is as clear as a bell that this is nonlocal filtration.

They were not wasting any time. In order to create the 245 entangled states, they had to make millions of tries.

I did not say they were wasting time. I said if as you suggested earlier, the "event-ready" information was available before the "experiment" (your definition), then it makes no sense for Alice(Bob) to measure the "bad" results -- that would be a waste of time. That they waited until *after* the measurement to filter out the "good" from the "bad" owes to the fact that the "good" signal was only available *after* the measurements had been made, which was my point all along. That is why it is *post*-selection.

 

[Heinera]

Nope they can't, there is no way for Alice (Bob) to know what "experiment" (your definition) is good in real time. Even if there was a way, there is no way to analyze any data in real time. Analysis requires the results from Alice and Bob to be brought together *after* the all the runs have been completed. This is obvious.

Alice and Bob don't need to know what experiment is good in real time, because it is not Alice and Bob that is doing the analysis. They are not real human beings, you know. Of course analysis can be done in real time before all the runs have been completed. It's just that as more runs come in, the analysis becomes more and more significant.

That is because you don't understand it. It simply is the fact that you need information from both Alice and Bob to filter the results at Alice, as well as the results at Bob. Therefore the filtered results are nonlocal. What is wrong in that? There is no way for Alice to know which of her results are "good" until the information she sends through the photon is compared with the information sent by Bob, and vice versa. it is as clear as a bell that this is nonlocal filtration.

Now it's clear that you don't understand the experiment. No information from the results at Alice or Bob is needed to filter the runs in this experiment. Only information from C is needed, which is available even before Alice and Bob have performed their run.

 

[wle]

I did not say they were wasting time. I said if as you suggested earlier, the "event-ready" information was available before the "experiment" (your definition), then it makes no sense for Alice(Bob) to measure the "bad" results -- that would be a waste of time. That they waited until *after* the measurement to filter out the "good" from the "bad" owes to the fact that the "good" signal was only available *after* the measurements had been made, which was my point all along. That is why it is *post*-selection.

Now it's clear that you don't understand the experiment. No information from the results at Alice or Bob is needed to filter the runs in this experiment. Only information from C is needed, which is available even before Alice and Bob have performed their run.

According to the text and Figure 2 of the ArXiv preprint [arXiv:1508.05949], the "go/no go" determination event is spacelike separated from Alice's and Bob's measurement choices and recording of outcomes, so the $C = \text{go/no go}$ outcome should neither causally influence nor be influenced by Alice's and Bob's measurement choices or results.

As far as Bell's theorem is concerned, at least one way you can formally accommodate the postselection is by considering it part of a three-party Bell scenario. Under the locality hypothesis, this means that the (single-round) joint probability distribution should factorise according to $$P(abc \mid xy) = \int \mathrm{d}\lambda \, \rho(\lambda) \, P_{\mathrm{A}}(a \mid x; \lambda) \, P_{\mathrm{B}}(b \mid y; \lambda) \, P_{\mathrm{C}}(c \mid \lambda) \,,$$ where $a, b, x, y$ are Alice's and Bob's inputs and outputs and $c \in \{\text{go}, \text{no go}\}$ is the event-ready outcome. From there, high school-level probability theory will tell you that conditioning on $c = \text{go}$ does not allow you to fake a nonlocal probability distribution between Alice and Bob's systems: $$\begin{eqnarray*}
P(ab \mid xy; c = \text{go}) &=& \frac{P(ab, c = \text{go} \mid xy)}{P(c = \text{go} \mid xy)} \\
&=& \int \mathrm{d}\lambda \, \rho(\lambda) \, \frac{P_{\mathrm{C}}(c = \text{go} \mid \lambda)}{P(c = \text{go})} \, P_{\mathrm{A}}(a \mid x; \lambda) \, P_{\mathrm{B}}(b \mid y; \lambda) \\
&=& \int \mathrm{d}\lambda \, \rho(\lambda \mid c = \text{go}) \, P_{\mathrm{A}}(a \mid x; \lambda) \, P_{\mathrm{B}}(b \mid y; \lambda) \,,
\end{eqnarray*}$$ which uses the no-signalling conditions (implied by locality) to say that $P(c = \text{go} \mid xy) = P(c = \mathrm{go})$ is independent of $x$ and $y$ and Bayes' theorem to say that $\rho(\lambda \mid c = \text{go}) = \rho(\lambda) \, \frac{P_{\mathrm{C}}(c = \text{go} \mid \lambda)}{P(c = \text{go})}$.

The end result, with the conditioning on "go", has the same local factorisation that is used in the (single round) derivation of Bell inequalities. (And from there, statistical analyses of the sort done by Gill and others explain how you can turn this into a hypothesis test applicable to a real multi-round Bell experiment.)

 

[DrChinese]

Without post-selection, there will be no swapping. You have to understand that swapping is precisely the process of selecting a sub-ensemble which is correlated in a specific way from a larger ensemble which is not correlated.

For example, take a set of pairs of numbers X,Y where the corresponding numbers of each pair (x,y) are related by y = sin(x). It follows that x and y are correlated. With two such such sets, say X1, Y1, and X2, Y2 randomly generated at space-like separated locations A and B. We could do an additional "measurement" z on each x, e.g. z = cos(x), giving a set of measurement results Z1 and Z2 at A and B respectively. There is no correlation between X1 and X2 and therefore no correlation between Y1 and Y2 or Z1 and Z2. For each pair (x,y) from each arm we send the y value to a distant location C, even before the z values are available. At C we simply compare the incoming values and if they are indistinguishable, we generate a "good" signal. Based on the RNG used at A and B, we may not have very many "good" signals but we will get a few. By post-selecting the Z1 and Z2 values using the "good" results from location C, we get a sub-ensemble of the Z1 and Z2 results which are correlated with each other. This is essentially the process of "swapping". Replace "correlation" with "entanglement" and you have "entanglement swapping". Perhaps the confusion is with the common practice of discussing the technique in the context of a single measurement as opposed to ensembles.

There is no way for Alice(Bob) to know which of their results are "good" without information going from both Alice and Bob to station C, and then the back to Alice (Bob) in the form of "good" signals.

BTW, local realists do not deny swapping, they believe swapping has a local realistic explanation.

Sorry, you DO deny that swapping is an essential requirement to CAUSING the entanglement. You equate swapping to detection (by definition), and I am saying you can detect without swapping.

Entanglement swapping = post-selection (B&C) + indistinguishability (B&C).

How do they check indistinguishability (B&C)? By looking for entanglement on A & D using the post selection group ONLY! There cannot be a local causal connection between the swapping and the A & D entanglement!

In other words: The local realist will have to admit that there is nothing occurring at A & D based on a decision made at B & C. But I can choose to post-select the A & D pairs using the B & C criteria WITH or WITHOUT having the B & C pairs be indistinguishable.

For example, I could place a linear polarizer in front of B and/or C. That should mean nothing to the local realist, since they believe the linear polarization is already determined. But for QM, that means that the photons B and C are distinguishable even though they otherwise will meet the post-selection criteria. There will be no entanglement at A & D, no violation of a Bell inequality.

Entanglement swapping is a physical process and is NOT just post-selection. It does require post-selection to determine whether swapping successfully occurred. The physical process (entanglement swapping) causes entanglement at A & D, demonstrating quantum non-locality.