- #1
BobF
- 2
- 1
- TL;DR Summary
- Angles are regarded as being dimensionless. We introduce a new dimension for angles and show how it works with traditional formulas.
Quickly estimate the value of this expression: sin(1.57). If your answer was about 1, then you assumed that 1.57 was a radian value. If your answer was about 0, you assumed that 1.57 was degrees. If you said that you can’t determine an answer, then you were expecting to see an angle expressed in either degrees or radians, not a bare number.
This is what a dimensionless entity looks like. There are no units. Rather than trying to invent dimensionless units, we will define a dimension for angles. It will work with the existing formulas that involve dimensionless angles. But perhaps it will give some additional clarity in some situations. I welcome opinions as to whether
We can easily see that angles have a dimension. The illustration that we will use throughout this document is this:
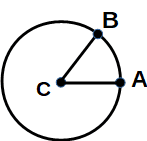Divide the circle into 360 equal intervals. The number of intervals between A and B is the number of degrees in the angle with vertex C. The circle is a dimension, the degrees is the measurement scale. This is a dimension.
This explanation will not satisfy many readers. The solution must fit within the metric system and the SI standard. Using the same diagram, give the radius CA a length of 1 meter; the arc AB also has a length of 1 meter. Then the angle ACB is 1 radian. Since the distance from A to B is measured along an arc rather than a straight line, we'll call its measure "arc meter" or "am". This is the base unit of measure for the circle dimension.
Now we use the traditional definition for angles. The number of radians in an angle is the arc length divided by the radius, or am/m. This is the base unit for the dimension Angle. Where the traditional formula m/m failed is that it did not acknowledge the need for the numerator to be measured on an arc. By making a Circle dimension with its measure "am" the arc requirement is retained in the formula.
About now some of you may be feeling a bit uneasy about this approach. Now that the whole structure is visible, let's look at a few details.
In SI each of the dimensions has a unique formula. While the unit "am" was introduced, the formula for deriving it is simply "m". Circle is a sub-dimension of the SI Length dimension. That means that "am" can be converted (with no conversion factor) to "m", but not the other way around (without additionial information not contained in the formula). Sub-dimensions is not a concept used elsewhere in SI. Whether it could be of value in other situations is beyond the scope of this document.
It is worth mentioning that the Angle dimension is also a sub-dimension of dimension 1. am/m converts to m/m which reduces to 1. But rather than manually placing a unit on a number, this approach provides a path to computing the radian measure.
One of the equations that is often cited as "proving" that angles are dimensionless is s = r θ. r is in meters and theta in radians. Evaluating the right side yields s in arc meters.
I am very interested in reactions to this proposal. Do you like it? Believe it? Would it be useful for you in your work? Would adding a dimension of this sort provide problems in the equations that you use? Would the am measure be beneficial to you? I look forward to your comments.
This is what a dimensionless entity looks like. There are no units. Rather than trying to invent dimensionless units, we will define a dimension for angles. It will work with the existing formulas that involve dimensionless angles. But perhaps it will give some additional clarity in some situations. I welcome opinions as to whether
We can easily see that angles have a dimension. The illustration that we will use throughout this document is this:
This explanation will not satisfy many readers. The solution must fit within the metric system and the SI standard. Using the same diagram, give the radius CA a length of 1 meter; the arc AB also has a length of 1 meter. Then the angle ACB is 1 radian. Since the distance from A to B is measured along an arc rather than a straight line, we'll call its measure "arc meter" or "am". This is the base unit of measure for the circle dimension.
Now we use the traditional definition for angles. The number of radians in an angle is the arc length divided by the radius, or am/m. This is the base unit for the dimension Angle. Where the traditional formula m/m failed is that it did not acknowledge the need for the numerator to be measured on an arc. By making a Circle dimension with its measure "am" the arc requirement is retained in the formula.
About now some of you may be feeling a bit uneasy about this approach. Now that the whole structure is visible, let's look at a few details.
In SI each of the dimensions has a unique formula. While the unit "am" was introduced, the formula for deriving it is simply "m". Circle is a sub-dimension of the SI Length dimension. That means that "am" can be converted (with no conversion factor) to "m", but not the other way around (without additionial information not contained in the formula). Sub-dimensions is not a concept used elsewhere in SI. Whether it could be of value in other situations is beyond the scope of this document.
It is worth mentioning that the Angle dimension is also a sub-dimension of dimension 1. am/m converts to m/m which reduces to 1. But rather than manually placing a unit on a number, this approach provides a path to computing the radian measure.
One of the equations that is often cited as "proving" that angles are dimensionless is s = r θ. r is in meters and theta in radians. Evaluating the right side yields s in arc meters.
I am very interested in reactions to this proposal. Do you like it? Believe it? Would it be useful for you in your work? Would adding a dimension of this sort provide problems in the equations that you use? Would the am measure be beneficial to you? I look forward to your comments.
