Dimensional Analysis Buckingham Pi Theorem

[Raddy13]

This is the problem I'm currently working on:

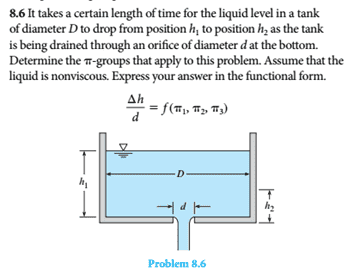
The pi groups I identified were h1, h2, d, D, g, t, and velocity, but when I looked at the solution, it selected Δh, D, t, ρ, d, ϒ, h1, with no explanation why those variables are needed. If I was solving with the Bernoulli equation, I wouldn't need density or specific weight, so why do those come up in this case? And if we're using all variables from the equation even if they're not relevant, then why doesn't pressure appear? The only explanation that the book gives is that "knowing what variables to choose requires experience" and then lists some common ones, but no explanation as to when they would be needed and when they wouldn't.

EDIT: Sorry, I meant to post this in the homework question forum.
<Moderator's note: Moved from a technical forum and thus no template.>

 

[scottdave]

What does ϒ represent? I would think that using combination of h1 and h2 could get the same result as h1 and Δh.

 

[Raddy13]

ϒ is specific weight (density times gravity).

It would end up with the same result, but since the one of the pi groups has to take the form of Δh/d, so Δh has to be one of the terms.

 

[JBA]

The liquid head pressure a the nozzle is a function of the density of the fluid.

 

[Chestermiller]

ϒ is specific weight (density times gravity).

It would end up with the same result, but since the one of the pi groups has to take the form of Δh/d, so Δh has to be one of the terms.

So the only parameter that they selected that you didn't select was $\rho$, right?

Incidentally, a terminology issue: The pi groups are the dimensionless groups, not the dimensional parameters.