Mohmmad Maaitah
- 90
- 20
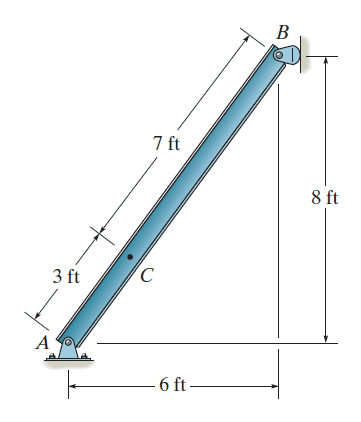
- Homework Statement
- The beam weighs 280 lb/ft. Determine the internal
normal force, shear force, and moment at point C.
- Relevant Equations
- Equations of equilibrium
I'm having problem in drawing the distributed load (weight per foot) for the inclined beam as it shows.
should it be rectangular? if so shouldn't the distributed load be vertical down as the resultant weight at the centroid (W)
 please help me understand how to draw the free body diagram for this one.
please help me understand how to draw the free body diagram for this one.
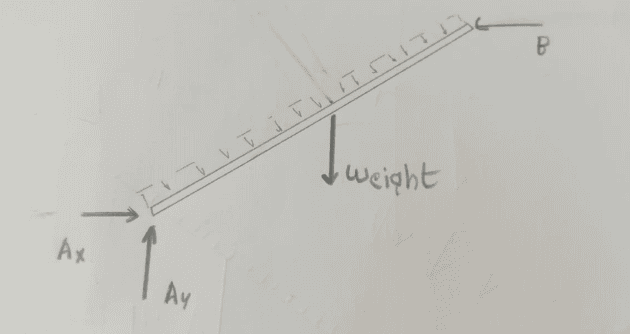
should it be rectangular? if so shouldn't the distributed load be vertical down as the resultant weight at the centroid (W)