Divide into 2 congruent pieces

[I like Serena]

Last time I asked for 5 congruent pieces.
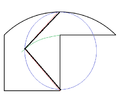
This time I'm only asking for 2.
\begin{tikzpicture}[ultra thick]
\draw (0,0) -- (-5,0) -- (-5,5);
\draw[rotate=-90] (0,0) -- (-5,0) -- (-5,5);
\draw (-5,5) arc (135:45:{5*sqrt(2)});
\end{tikzpicture}

 

[maxkor]

Spoiler

View attachment 7896

 

[I like Serena]

As before, that's a perfect solution maxkor.
Thank you for your participation!

Spoiler

For the record, this problem depends on rotational symmetry, while the https://mathhelpboards.com/challenge-questions-puzzles-28/divide-into-5-congruent-pieces-23597.html was about translational symmetry.
They are really a set.
It also means that we can just as easily divide it into 5 congruent pieces:
\begin{tikzpicture}[ultra thick]
\draw (0,0) -- (-5,0) -- (-5,5);
\draw[rotate=-18] (0,0) -- (-5,0) -- (-5,5);
\draw[rotate=-36] (0,0) -- (-5,0) -- (-5,5);
\draw[rotate=-54] (0,0) -- (-5,0) -- (-5,5);
\draw[rotate=-72] (0,0) -- (-5,0) -- (-5,5);
\draw[rotate=-90] (0,0) -- (-5,0) -- (-5,5);
\draw (-5,5) arc (135:45:{5*sqrt(2)});
\end{tikzpicture}

I actually left a hint in the TikZ picture itself by using the rotate property, although I kind of doubt that anyone noticed. (Wink)