Double Integral Cartesian to Polar Coordinates

[jerzey101]

Homework Statement

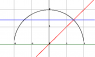
Use polar coordinates to evaluate:
∫^sqrt(2)₀ ∫^sqrt(4-y2)_y 1/(1+x²+y²) dxdy

Homework Equations

The Attempt at a Solution

I graphed it and I see r is the part of the elipse sqrt(4-y²) and goes from 0 to ∏/4. I'm not sure how to make the bounds for r or how to covert the function to polar. Does it just convert to 1/(1+r²), then add the conversion factor r?
∫^∏/4₀ ∫^?_? 1/(1+r²) r drdθ

 

[DryRun]

Use LaTeX formatting to make your integrals clearer and easier to understand.

Your double integral looks like this:
$$\int^{y=\sqrt 2}_{y=0} \int^{x=\sqrt {4-y^2}}_{x=y} \frac{1}{1+x^2+y^2} \,.dxdy$$
You have to plot the limits to see the area required and hence deduce the correct polar limits.
First, convert: $x=\sqrt {4-y^2}$ into a simpler form. This gives you: $x^2+y^2=4$, which is a circle with center (0,0) and radius = 2. The other limits are obvious.

I have attached the graph. If you are having trouble deducing the region required from the limits, save the graph, edit/shade it to show the required area and then attach it to your reply.

 

[jerzey101]

I'm just not sure what to put for the r limits. I know it is 0 to the circle x²+y²=4. So is it just 0 to 2?

 

[DryRun]

I'm just not sure what to put for the r limits. I know it is 0 to the circle x²+y²=4. So is it just 0 to 2?

You're correct.

 

[jerzey101]

Thanks!
I think I figured it all out now. Thanks again.