B Doubt on an EM problem regarding gauss law

[ubergewehr273]

There's this problem 2.18 in the book "Introduction to electrodynamics" by Griffith.
The problem says the following,
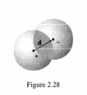
"Two spheres, each of radius R and carrying uniform charge densities $+\rho$ and $-\rho$, respectively, are placed so that they partially overlap (Image_01). Call the vector from the positive center to the negative center d. Show that the field in the region of overlap is constant, and find its value."

Well, I was able to solve the problem as expected from the book, however, I wondered why the field in the region of overlap has to be a non-zero quantity. I could very well take a spherical Gaussian surface that resides inside the region of overlap, and since the net charge enclosed in this region is 0, hence the electric field ought to be zero (refer Image_02). Where am I going wrong over here?

PFA the corresponding images.

 

[dRic2]

$\int \mathbf E \cdot d \mathbf a$ is a surface integral. You can "take outside" the absolute value of E only under particular condition of symmetries (pay attention to the dot product between $\mathbf E$ and the surface element $d \mathbf a$). For example, in spherical coordinates the field inside the surface has to be radial. Here it is most certainly not radial: it is constant! It is explained in the book that you have to pay attention to symmetries when using gauss law.

$\int \mathbf E \cdot d \mathbf a = 0$ does not necessarily imply $\mathbf E = 0$. Take for example a point charge and apply gauss law to a surface that does NOT contain the charge. According to you reasoning you would be tempted to say that the field inside the surface is zero while it is obviously not zero.

 

[ubergewehr273]

∫E⋅da=0\int \mathbf E \cdot d \mathbf a = 0 does not necessarily imply E=0\mathbf E = 0. Take for example a point charge and apply gauss law to a surface that does NOT contain the charge. According to you reasoning you would be tempted to say that the field inside the surface is zero while it is obviously not zero.

Thanks for the insight :)