Draw a NAND-gate to get that output

[mathmari]

Hey!

I want to draw a circuit that has four inputs a, b, c, d, and which gives the value $[(a \lor b) \lor (c \lor \neg d)] \land (c \land \neg a)$ at the output, using exclusively the NAND gates with two inputs.
Hint: If you connect the two inputs of such a NAND gate, you get a so-called inverter, i.e. a circuit implementation of the logical negation.

The NAND-gate is:

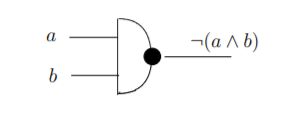
I have done the following:
\begin{align*}[(a\lor b)\lor (c\lor \neg d)]\land (c\land \neg a)&=[\neg (\neg a\land \neg b)\lor \neg (\neg c\land d)]\land (c\land \neg a)\\ & =\neg [(\neg a\land \neg b)\land (\neg c\land d)]\land (c\land \neg a)\end{align*}
We can get the part $\neg [(\neg a\land \neg b)\land (\neg c\land d)]$ using the NAND gate, right? What about the second part? Do we have to write it in an other way? :unsure:

 

[I like Serena]

We can get the part $\neg [(\neg a\land \neg b)\land (\neg c\land d)]$ using the NAND gate, right? What about the second part? Do we have to write it in an other way?

Hey mathmari!

Yep.
We can apply inverters both before and after a NAND gate can't we?
That is, we can write $x\land y$ as $\lnot\lnot(x\land y)$ can't we?

 

[mathmari]

We can apply inverters both before and after a NAND gate can't we?
That is, we can write $x\land y$ as $\lnot\lnot(x\land y)$ can't we?

I got stuck right now. We have that \begin{align*}[(a\lor b)\lor (c\lor \neg d)]\land (c\land \neg a)&=[\neg (\neg a\land \neg b)\lor \neg (\neg c\land d)]\land (c\land \neg a)\\ & =\neg [(\neg a\land \neg b)\land (\neg c\land d)]\land (c\land \neg a) \\ & = [(\neg a\land \neg b) \text{ NAND } (\neg c\land d)]\land (c\land \neg a)\end{align*}

Now we have to write $\neg a\land \neg b$ in terms of $\text{ NAND } $.

So do we have to write the negartion $\neg$ in terms of $\text{ NAND } $ ? :unsure:

 

[I like Serena]

Yes.
Consider the hint that was given in the problem statement: "Hint: If you connect the two inputs of such a NAND gate, you get a so-called inverter."

 

[mathmari]

Yes.
Consider the hint that was given in the problem statement: "Hint: If you connect the two inputs of such a NAND gate, you get a so-called inverter."

We have the following:
\begin{align*}&\neg a=\neg (a\land a)=a \text{ NAND } a \\ & \neg b=\neg (b\land b)=b \text{ NAND } b \\ & \neg c=\neg (c\land c)=c \text{ NAND } c\end{align*}

Therefore we get \begin{align*}[(a\lor b)\lor (c\lor \neg d)]\land (c\land \neg a)&=[\neg (\neg a\land \neg b)\lor \neg (\neg c\land d)]\land (c\land \neg a)\\ & =\neg [(\neg a\land \neg b)\land (\neg c\land d)]\land (c\land \neg a) \\ & = [(\neg a\land \neg b) \text{ NAND } (\neg c\land d)]\land (c\land \neg a) \\ & = [([a \text{ NAND } a ]\land [b \text{ NAND } b]) \text{ NAND } ([c \text{ NAND } c]\land d)]\land (c\land [a \text{ NAND } a ])\end{align*}

Is everything correct so far? How could we continue? I am a bit confused how we get the $\neg$ before an expression to get $\text{NAND}$ without losing $\land$. Could you give me a hint? :unsure:

 

[I like Serena]

Is everything correct so far? How could we continue? I am a bit confused how we get the $\neg$ before an expression to get $\text{NAND}$ without losing $\land$. Could you give me a hint?

It looks correct to me.
Did you consider that $x\land y=\lnot\lnot(x\land y)=\lnot(x \operatorname{NAND} y) = (x \operatorname{NAND} y) \operatorname{NAND}\, (x \operatorname{NAND} y) $?

 

[mathmari]

It looks correct to me.
Did you consider that $x\land y=\lnot\lnot(x\land y)=\lnot(x \operatorname{NAND} y) = (x \operatorname{NAND} y) \operatorname{NAND}\, (x \operatorname{NAND} y) $?

Ok!

We have the following:
\begin{align*}&\neg a=\neg (a\land a)=a \text{ NAND } a \\ & \neg b=\neg (b\land b)=b \text{ NAND } b \\ & \neg c=\neg (c\land c)=c \text{ NAND } c \\ & x\land y=\lnot\lnot(x\land y)=\lnot(x \operatorname{NAND} y) = (x \operatorname{NAND} y) \operatorname{NAND}\, (x \operatorname{NAND} y)\end{align*}

Therefore we get \begin{align*}&[(a\lor b)\lor (c\lor \neg d)]\land (c\land \neg a)=[\neg (\neg a\land \neg b)\lor \neg (\neg c\land d)]\land (c\land \neg a)\\ & =\neg [(\neg a\land \neg b)\land (\neg c\land d)]\land (c\land \neg a) \\ & = [(\neg a\land \neg b) \text{ NAND } (\neg c\land d)]\land (c\land \neg a) \\ & = [([a \text{ NAND } a ]\land [b \text{ NAND } b]) \text{ NAND } ([c \text{ NAND } c]\land d)]\land (c\land [a \text{ NAND } a ]) \\ & = [(([a \text{ NAND } a ] \operatorname{NAND} [b \text{ NAND } b]) \operatorname{NAND}\, ([a \text{ NAND } a ] \operatorname{NAND} [b \text{ NAND } b])) \text{ NAND } ([c \text{ NAND } c] \operatorname{NAND} d) \operatorname{NAND}\, ([c \text{ NAND } c] \operatorname{NAND} d)]\land ((c \operatorname{NAND} [a \text{ NAND } a ]) \operatorname{NAND}\, (c \operatorname{NAND} [a \text{ NAND } a ])) \\ & = ([(([a \text{ NAND } a ] \operatorname{NAND} [b \text{ NAND } b]) \operatorname{NAND}\, ([a \text{ NAND } a ] \operatorname{NAND} [b \text{ NAND } b])) \text{ NAND } ([c \text{ NAND } c] \operatorname{NAND} d) \operatorname{NAND}\, ([c \text{ NAND } c] \operatorname{NAND} d)]\text{ NAND} ((c \operatorname{NAND} [a \text{ NAND } a ]) \operatorname{NAND}\, (c \operatorname{NAND} [a \text{ NAND } a ])))\text{ NAND } ([(([a \text{ NAND } a ] \operatorname{NAND} [b \text{ NAND } b]) \operatorname{NAND}\, ([a \text{ NAND } a ] \operatorname{NAND} [b \text{ NAND } b])) \text{ NAND } ([c \text{ NAND } c] \operatorname{NAND} d) \operatorname{NAND}\, ([c \text{ NAND } c] \operatorname{NAND} d)]\text{ NAND} ((c \operatorname{NAND} [a \text{ NAND } a ]) \operatorname{NAND}\, (c \operatorname{NAND} [a \text{ NAND } a ])))\end{align*}

Is it possible to simply that expression or shoud we have simplied it before the last step? :unsure:

Or is that the answer, since the exercise asks to draw the gate? :unsure:

 

[I like Serena]

Is it possible to simply that expression or shoud we have simplied it before the last step?
Or is that the answer, since the exercise asks to draw the gate?

I think we should draw the circuit.
The same expressions occur many times, and instead of repeating them, we should reuse them.

 

[mathmari]

I think we should draw the circuit.
The same expressions occur many times, and instead of repeating them, we should reuse them.

The last expression of #7 is so confusing, this last one is the one that I have to draw, or which expression should I consider?
I have to start with all small expressions and then getting to the larger ones, right? :unsure:

 

[I like Serena]

The last expression of #7 is so confusing, this last one is the one that I have to draw, or which expression should I consider?
I have to start with all small expressions and then getting to the larger ones, right?

I'd recommend starting with an expression in which the expressions of the form $\lnot x$ have not been expanded yet to $x \operatorname{NAND} x$.
Because that is where $x$ is getting duplicated while in a drawing we only want to see $x$ once.

 

[mathmari]

I'd recommend starting with an expression in which the expressions of the form $\lnot x$ have not been expanded yet to $x \operatorname{NAND} x$.
Because that is where $x$ is getting duplicated while in a drawing we only want to see $x$ once.

So do we consider the expression $[(\neg a\land \neg b) \text{ NAND } (\neg c\land d)]\land (c\land \neg a)$ ?

Or do we expand the $\land$ and get $\left [[(\neg a\land \neg b) \text{ NAND } (\neg c\land d)] \text{ NAND } (c\land \neg a)\right ] \text{ NAND } \left [[(\neg a\land \neg b) \text{ NAND } (\neg c\land d)] \text{ NAND } (c\land \neg a)\right ]$ ?

:unsure:

 

[I like Serena]

So do we consider the expression $[(\neg a\land \neg b) \text{ NAND } (\neg c\land d)]\land (c\land \neg a)$ ?

Or do we expand the $\land$ and get $\left [[(\neg a\land \neg b) \text{ NAND } (\neg c\land d)] \text{ NAND } (c\land \neg a)\right ] \text{ NAND } \left [[(\neg a\land \neg b) \text{ NAND } (\neg c\land d)] \text{ NAND } (c\land \neg a)\right ]$ ?

:unsure:

How about $\lnot\Big[\big[\lnot(\neg a \text{ NAND } \neg b) \text{ NAND } \lnot(\neg c \text{ NAND } d)\big] \text{ NAND } \big[\lnot(c \text{ NAND } \neg a)\big]\Big]$?

 

[mathmari]

How about $\lnot\Big[\big[\lnot(\neg a \text{ NAND } \neg b) \text{ NAND } \lnot(\neg c \text{ NAND } d)\big] \text{ NAND } \big[\lnot(c \text{ NAND } \neg a)\big]\Big]$?

So we get:

Is that correct? Is there an online program that we could draw the above? :unsure:

 

[I like Serena]

Is that correct? Is there an online program that we could draw the above?

Let's start with $\lnot a\text{ NAND }\lnot b$.
You have a NAND to find $\lnot a$.
Shouldn't you also have a NAND to find $\lnot b$ before combining it with $\lnot a$?

An online drawing program for circuits with logic ports...
TikZ comes to mind, which has dedicated libraries for logic ports.
I found for instance this overflow article which mentions circuitikz.

We can use the http://35.164.211.156/tikz/tikzlive.html we have on MHB to edit such a picture.
Let's see...
\begin{tikzpicture}
%preamble \usepackage{circuitikz}
%preamble \usepackage{amsmath}
\coordinate[label=left:a] (a) at (0,2);
\coordinate[label=left:b] (b) at (0,0);
\draw (2,2) node[nand port] (nota) {};
\draw (2,0) node[nand port] (notb) {};
\draw (4,1) node[nand port] (nand1) {};
\draw (a) -- (nota.in 1);
\draw (a) -- (nota.in 2);
\draw (b) -- (notb.in 1);
\draw (b) -- (notb.in 2);
\draw (nota.out) -- (nand1.in 1);
\draw (notb.out) -- (nand1.in 2);
\draw (nand1.out) node[above right] {$\lnot a\text{ NAND }\lnot b $};
\end{tikzpicture}

\begin{tikzpicture}
  %preamble \usepackage{circuitikz}
  %preamble \usepackage{amsmath}
  \coordinate[label=left:a] (a) at (0,2);
  \coordinate[label=left:b] (b) at (0,0);
  \draw (2,2) node[nand port] (nota) {};
  \draw (2,0) node[nand port] (notb) {};
  \draw (4,1) node[nand port] (nand1) {};
  \draw (a) -- (nota.in 1);
  \draw (a) -- (nota.in 2);
  \draw (b) -- (notb.in 1);
  \draw (b) -- (notb.in 2);
  \draw (nota.out) -- (nand1.in 1);
  \draw (notb.out) -- (nand1.in 2);
  \draw (nand1.out) node[above right] {$\lnot a\text{ NAND }\lnot b $};
\end{tikzpicture}

 

[mathmari]

Let's start with $\lnot a\text{ NAND }\lnot b$.
You have a NAND to find $\lnot a$.
Shouldn't you also have a NAND to find $\lnot b$ before combining it with $\lnot a$?

An online drawing program for circuits with logic ports...
TikZ comes to mind, which has dedicated libraries for logic ports.
I found for instance this overflow article which mentions circuitikz.

We can use the http://35.164.211.156/tikz/tikzlive.html we have on MHB to edit such a picture.

I used the online editor of MHB and I got:

https://www.physicsforums.com/attachments/311767._xfImportIs everything correct? :unsure:

Is it understanadle like that or should I write at each gate the output? :unsure:

 

[I like Serena]

It looks correct to me.
And I could check the circuit based on the expression on the right, so I believe that is good enough.

 

[mathmari]

It looks correct to me.
And I could check the circuit based on the expression on the right, so I believe that is good enough.

Great! Thanks a lot!