Dynamic system of self balancing robot

[JVDC]

Homework Statement

Calculate the torque (Moment around joint in middle of foot) at which the robot starts tipping over its front foot.

Relevant Equations

Newton

Hello everyone.

I'm stuck on my robotics homework. Can anyone help me?

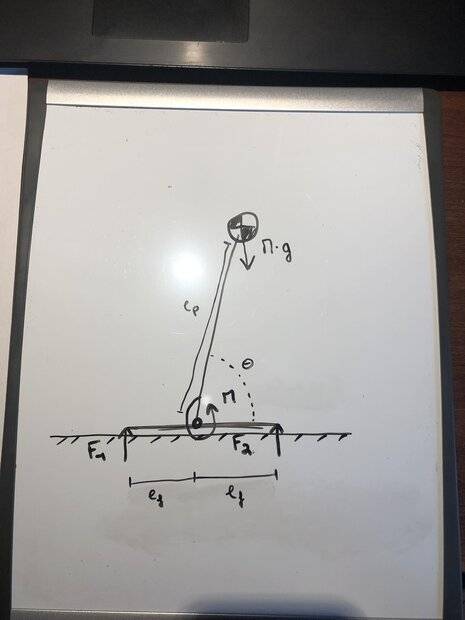
I have a stick with a certain mass on it. This stick is like an inverted pendulum. It can rotate around an ankle joint in the middle of the foot. The foot is placed on the ground. Suppose the stick to have no mass. There is a figure attached to be more clear.

If I push the stick forwards, a moment will act on it in the joint that is linear with Θ. Its equation is M = k2 * r_e2 * (90° - Θ - ΔΘ). It is a spring that is unidirectional, so its moment can never be negative. So, it is logical to assume that the robot will never tip around the rear of the foot, as no moment can 'lock' the foot.

The forces F₁ and F₂ can also never be negative, as the foot does not stick on the ground. So, the robot tips around the front of the foot when F₁ = 0. The system is dynamic, so the stick can already rotate with a certain velocity.

Now, how can I calculate at which ankle moment the robot tips?

I already have the following equations.
F₁ + F₂ = M*g
I * Θ^'' = -M*g*l_p * cosΘ + k2 * r_e2 * (90° - Θ - ΔΘ) - F₁*l_f + F₂*l_f

What other equations can I use?

 

[Lnewqban]

Welcome, @JVDC !

If I understand your question, you need to calculate the greatest moment at the ankle which still does not lift one of the edges of the foot.
The angular acceleration of the leg-mass must be considered, unless the movements are slow.

 

[haruspex]

What other equations can I use?

If it is starting to tip, what can you say about $F_1$ and $F_2$?

 

[JVDC]

I suppose that F_1 will equal zero. Then I can say that F_2 equals M*g, but I think I’m still missing something…

 

[haruspex]

I suppose that F_1 will equal zero. Then I can say that F_2 equals M*g, but I think I’m still missing something…

Your notation is a bit confusing. You have M meaning two things and do not define some variables.
As @Lnewqban points out, there is an ambiguity in the question. There is a difference between a slowly increasing torque and one suddenly applied in the upright position. In the latter case, there will be a build up of angular momentum while the spring torque increases. It is analogous to the difference between lowering a mass suspended from spring to its equilibrium point versus letting it go from the relaxed spring position.

If you only want to know at what steadily increased torque it will start to tip, you do not care about the acceleration and you do not need $\Delta\theta$. Just write the torque balance equation for the case where $F_1=0$.