DTskkaii
- 19
- 0
Question:
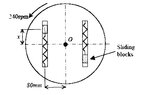
The flat circular disc rotates about a vertical axis through O with a constant angular velocity of 240rpm. Prior to rotation, each of the 0.5kg sliding blocks has the position x=25mm with no force in its attached spring. Each spring has a stiffness of 400N/m, Neglect any friction between the blocks and the slots, and neglect the mass of the springs.
(a) Determine the value of x for each spring
(b) Calculate the normal force N exerted by the side of the slot on the block
I have attached the diagram.
Relevant equations
Not yet completely sure. If someone knows of a resource towards rotational velocity, that would be helpful, but I will update this section as soon as I have identified appropriate equations.
The attempt at a solution
As per above, I will upload something as soon as I can get a solid attempt down. I'm honestly incredibly lost on this question, it just seems like there are so many aspects happening at once.
The flat circular disc rotates about a vertical axis through O with a constant angular velocity of 240rpm. Prior to rotation, each of the 0.5kg sliding blocks has the position x=25mm with no force in its attached spring. Each spring has a stiffness of 400N/m, Neglect any friction between the blocks and the slots, and neglect the mass of the springs.
(a) Determine the value of x for each spring
(b) Calculate the normal force N exerted by the side of the slot on the block
I have attached the diagram.
Relevant equations
Not yet completely sure. If someone knows of a resource towards rotational velocity, that would be helpful, but I will update this section as soon as I have identified appropriate equations.
The attempt at a solution
As per above, I will upload something as soon as I can get a solid attempt down. I'm honestly incredibly lost on this question, it just seems like there are so many aspects happening at once.