Thermofox
- 144
- 26
- Homework Statement
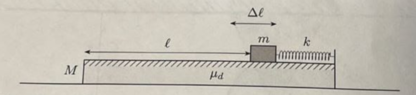
- A block, with mass ##m_b = 1 kg##, is placed on a slab, with mass ##m_s= 4 kg##, which is able to slide without friction on the horizontal plane on which it is placed, as shown in the Figure. There is friction between the body and the slab characterized by a coefficient of dynamic friction ##μ_d=0.2##. The body is initially placed at the left end of an ideal spring, with elastic constant ##k = 600 N/m##, whose right end is fixed to the right end of the slab. The spring, initially compressed by ##Δl = 5 cm##, at a certain instant is released to expand freely. Assuming the bodies are initially at rest and knowing that the distance separating the body of mass m from the left edge of the slab is ##l = 20 cm##
- Relevant Equations
- ##\Sigma F = ma##
I need to determine:
1) The accelerations of both the slab and the block, the moment right after the spring was released.
=> I can consider Fspring as a constant force. Both bodies can be considered as points of mass.
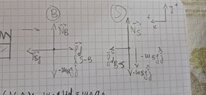
I'm taking as positive the left direction. I've analyzed both objects using the free body diagram and found that:
$$\begin{cases}
F_{spring}-f_d=m_b a_b \\
f_d= m_s a_s \\
f_d= \mu_d m_b g \\
\Sigma F_y=0
\end{cases}$$
From this system I can determine both accelerations since I know everything, except them.
$$\begin{cases}
k \Delta l - \mu_d m_b g = m_b a_b \\
m_b \mu_d g= m_s a_s
\end{cases}$$
##\begin{cases}
a_b= \frac {k \Delta l - m_b g \mu_d} {m_b} = \frac {(600) (0.05) - (1)(9.81)(0.2)} 1 = 28.0 \frac m {s^2} \\
a_s= \frac {m_b g \mu_d} {m_s}= \frac {(1)(9.81)(0.2)} {4}= 0.49 \frac m {s^2}
\end{cases}##
2)The velocities of both the block and the slab, when the block reaches the left edge of the slab.
Here I've tried using an energy balance equation:
##ΔE_m=W_{\text{non conservative forces}}##
=> ##\frac 1 2 m_s v_{s,f}^2 + \frac 1 2 m_b v_{b,f}^2 - \frac 1 2 k \Delta l^2 = - W_{\text{friction}}##
But I don't know how to go forward, since I have 2 unknowns ##(v_{b,f};v_{s,f})## but only one equation.
I thought of maybe finding ##v_{s,f}## by observing that the slab is under the action of a constant force ##f_d## (since ##f_d## depends only by the mass of the block). Therefore the slab moves in a uniformly accelerated motion, but I neither have the final time nor the final position.
1) The accelerations of both the slab and the block, the moment right after the spring was released.
=> I can consider Fspring as a constant force. Both bodies can be considered as points of mass.
I'm taking as positive the left direction. I've analyzed both objects using the free body diagram and found that:
$$\begin{cases}
F_{spring}-f_d=m_b a_b \\
f_d= m_s a_s \\
f_d= \mu_d m_b g \\
\Sigma F_y=0
\end{cases}$$
From this system I can determine both accelerations since I know everything, except them.
$$\begin{cases}
k \Delta l - \mu_d m_b g = m_b a_b \\
m_b \mu_d g= m_s a_s
\end{cases}$$
##\begin{cases}
a_b= \frac {k \Delta l - m_b g \mu_d} {m_b} = \frac {(600) (0.05) - (1)(9.81)(0.2)} 1 = 28.0 \frac m {s^2} \\
a_s= \frac {m_b g \mu_d} {m_s}= \frac {(1)(9.81)(0.2)} {4}= 0.49 \frac m {s^2}
\end{cases}##
2)The velocities of both the block and the slab, when the block reaches the left edge of the slab.
Here I've tried using an energy balance equation:
##ΔE_m=W_{\text{non conservative forces}}##
=> ##\frac 1 2 m_s v_{s,f}^2 + \frac 1 2 m_b v_{b,f}^2 - \frac 1 2 k \Delta l^2 = - W_{\text{friction}}##
But I don't know how to go forward, since I have 2 unknowns ##(v_{b,f};v_{s,f})## but only one equation.
I thought of maybe finding ##v_{s,f}## by observing that the slab is under the action of a constant force ##f_d## (since ##f_d## depends only by the mass of the block). Therefore the slab moves in a uniformly accelerated motion, but I neither have the final time nor the final position.
Attachments
Last edited: