Dyson equation and Feynman diagrams: a brief explain

[FrancescoS]

Hi!
I have found a note about Generating functionals that seems to be very direct.
Since I faced a difficulty many times without solve it, I would like if anyone can explain me my troubles.
You can fine the note here (link).
In the following figure, the author describes the 3-point green function in the way it's defined

I don't understand what does it mean exactly "(more vertices)" and the 2 factor in front of the three-vertex. Does "more vertices" stands for other possibles interaction vertices, like $\phi^4$ etc…?
And the 2 factor? I should expect a factor of $3!$.

Starting from this 2-factor, he prefers to write the above equation using this decomposition

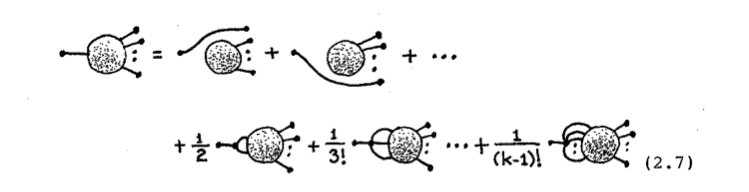Can you explain it in a more detailed way? What does the combinatoric factors comes from? I would like to understand it once for all.

There is also this diagram, where $Z[J]$ is the generating functional of green functions.

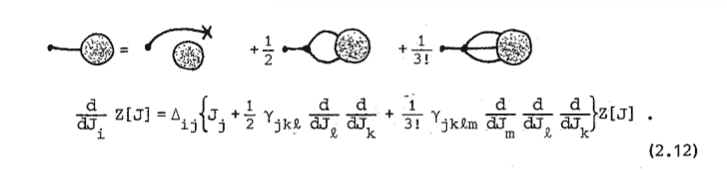
If I use the definition of $Z[J]$ that is

$Z[J] = \Sigma_{n = 0}^{+ \infty} \frac{i^n}{n!}\int dx_1 … dx_n G(x_1,…,x_n)J(x_1)…J(x_n)$

and if I perform the functional derivative

$\frac{\delta Z[J]}{\delta J(y_1)} = \Sigma_{n=1}^{+ \infty}\frac{i^n}{(n-1)!}\int dx_1…dx_{n-1}G(x_1,…,x_{n-1},y_1)J(x_1)…J(x_n)$
and I would like to obtain the expression he writes below, but i don't manage to do it.

Any help?? Thank you

 

[eljose79]

Hi there,

I would be happy to explain the concept of generating functionals and how they relate to the 3-point green function in more detail.

First, let's define what a generating functional is. A generating functional is a mathematical function that can be used to generate a series of functions. In the context of quantum field theory, a generating functional is used to generate the correlation functions, or in this case, the green functions.

Now, let's take a look at the 3-point green function. This function describes the amplitude for three particles to interact with each other. The "more vertices" in the equation refers to the possibility of having more than three particles interacting with each other. In quantum field theory, this can be represented by different interaction vertices, such as the $\phi^4$ vertex, as you mentioned.

The 2 factor in front of the three-vertex is a combinatoric factor. In this case, it represents the number of ways in which the three particles can interact with each other. In general, for a three-vertex, there are 3! = 6 possible ways for the particles to interact. However, the 2 factor takes into account the fact that the particles are indistinguishable, so some of these interactions are equivalent. Hence, we only need to consider 2 of the 6 possible interactions.

Now, let's move on to the decomposition of the equation. This is simply a way of rearranging the terms in the equation to make it easier to work with. The combinatoric factors come from the fact that we are considering all possible combinations of the particles interacting with each other. The expression below the diagram is simply the result of performing the functional derivative on the generating functional, as you have correctly stated.

I hope this explanation helps to clarify your understanding of generating functionals and the 3-point green function. Let me know if you have any further questions. Good luck with your research!