Electric field external to Conducting Hollow Sphere with charge inside

[curious_mind]

Homework Statement

Given a conducting metallic Hollow sphere as shown in the figure. A point charge is placed at distance $p$ from its center. What is the magnitude of electric field at a point away at distance $a$ from its center on the same line, as shown in the figure?

Relevant Equations

The electric field inside the conducting metallic hollow sphere is zero.

I have read Griffiths' Chapter 2 sections on Conductors. According to it, (if I understood it correctly) if the charge is put inside the cavity of a conductor, then the equal and opposite total charge will be induced surrounding the cavity. This charge and the total charge induced surrounding the cavity will be such that the total electric field will be canceled out inside the conductor. Then the total charge will be induced again on the surface of the conductor. So that the field outside the conductor will be due to a point charge placed inside the cavity.

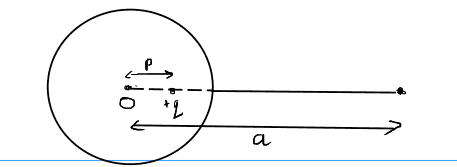
But I do NOT think this argument applies to the hollow conducting sphere. Because due to point charge $q$ placed inside the hollow conducting sphere, equal and opposite total charge $-q$ will be induced to the surface of the hollow conducting sphere, is it correct? So I think the electric field inside the hollow metallic conducting sphere will NO LONGER be 0. (Is this reasoning correct, or where Is it mistaken ?)

So, if we take Gaussian surface covering a hollow sphere and a point charge with a radius greater than the given sphere's radius, then the total charge enclosed will be zero.
$$ \oint_{S} \vec{\mathbf{E}} \cdot d\vec{\mathbf{A}} = \dfrac{Q_{enc}}{\varepsilon_0} = \dfrac{q-q}{\varepsilon_0} = 0$$
So, I think at any point external to the given hollow sphere and point charge inside it, electric field should be ZERO.

But, The answer given as $\vec{\mathbf{E}}_{outside} = \dfrac{1}{4 \pi \epsilon_0} \dfrac{q}{a^2} \hat{r}$. Remarkable thing is, the direction also given away from the sphere, means the field will be of repulsive nature. It is not due to induced negative charge then, otherwise direction would be opposite. I do not understand how it comes, can anyone help me? Is the answer given WRONG ?

 

[kuruman]

The given answer is not wrong.

The hollow sphere has two surfaces, one inside and one outside at a larger radius. The difference in radii is the non-zero thickness of the shell. If the conductor is initially neutral, placing charge +Q inside will induce total charge -Q on the inner surface of the shell. This will leave total charge +Q on the outer surface.

You can see why that is if you use Gauss's law correctly. You know that the electric field inside the conductor material is zero. Gauss's law for the sphere says $$\int_S \mathbf{E}\cdot \mathbf{\hat n}~dA=\frac{q_{enc.}}{\epsilon_0}.$$ If the Gaussian surface is a sphere of radius between the inner and outer radius of the shell, the left hand side is zero because $\mathbf{E}=0$ inside the conductor. This means that $q_{enc}=0.$ But you know that there is already charge $+Q$ at the center. To get zero enclosed charge, you must have $-Q$ on the inner surface.

Having established that, draw another Gaussian surface of radius larger than the outer radius of the shell. Since the shell itself is neutral to begin with, the enclosed charge must be $+Q$. But you know that there is $+Q$ at the center and total charge $-Q$ on the inner surface. It follows that the outer surface must have total charge $+Q$

Take home message: The electric field due to a charged conducting sphere in the region outside its outer radius and inside its inner radius is that of a point charge at the center of the sphere. In the region between the two radii the electric field is zero.

 

[curious_mind]

Well, If we take hollow sphere having two surfaces, then I understand that the situation will be similar to charge put inside a cavity of a conductor. And the answer will be followed. But that precisely is my dissatisfaction. What if we take thickness of the shell to be zero. An ideal situaiton where hollow sphere only has one surface. What will happen then ?

 

[PhDeezNutz]

Although you are in chapter 2 it might be helpful to skim chapter 3. Specifically section 3.2.4 where the method of images for a sphere is covered.

This is the same problem as the one covered in 3.2.4 but inverted so you'll have to make a change of variables but once you do that it will be solved.

 

[BvU]

Well, If we take hollow sphere having two surfaces, then I understand that the situation will be similar to charge put inside a cavity of a conductor. And the answer will be followed. But that precisely is my dissatisfaction. What if we take thickness of the shell to be zero. An ideal situaiton where hollow sphere only has one surface. What will happen then ?

That's not an ideal situation, because in that case there can be no conduction. The essence of using a gauss pillbox at the surface of a conductor is that the electric field lines are perpendicular to the surface. The surface charge distributes in such a way that this is ensured. With no other charges present outside the spherical shell, this means the outside surface charge is evenly distributed. But on the inner side, the surface charge distribution is only evenly distributed if the extra charge is at the exact center.

$\$

 

[curious_mind]

That's not an ideal situation, because in that case there can be no conduction. The essence of using a gauss pillbox at the surface of a conductor is that the electric field lines are perpendicular to the surface. The surface charge distributes in such a way that this is ensured. With no other charges present outside the spherical shell, this means the outside surface charge is evenly distributed. But on the inner side, the surface charge distribution is only evenly distributed if the extra charge is at the exact center.

$\$

You mean that it is not ideal to consider thickness of the shell zero ? Even if it would, it would no longer be a conductor ?

 

[BvU]

Correct.

 

[curious_mind]

Correct.

Then what about conducting plates of capacitor ? We take them infinitesimally thin long metallic plates, right ?

 

[BvU]

No we do not. Who says so ?

 

[curious_mind]

No we do not. Who says so ?

Ok I think I do understand your point. I will get back again after some pondering.

I just looked at diagrams in this link, which are having finite thickness.

EDIT : There was a wrong link I cited previously, here is the link
https://www.physicsforums.com/threa...wo-conducting-plates-using-gauss-law.1053894/

 

[kuruman]

Ok I think I do understand your point. I will get back again after some pondering.

I just looked at diagrams in this link, which are having finite thickness https://www.physicsforums.com/members/matinsar.699283/

That's a link to a user not a thread.

 

[curious_mind]

That's a link to a user not a thread.

Oh my bad, really sorry.
https://www.physicsforums.com/threa...wo-conducting-plates-using-gauss-law.1053894/

 

[kuruman]

Oh my bad, really sorry.
https://www.physicsforums.com/threa...wo-conducting-plates-using-gauss-law.1053894/

I hope that the thread you quoted helped your understanding.

 

[curious_mind]

I hope that the thread you quoted helped your understanding.

Yes, but my confusion is not Gauss' law. The thread is helpful to me because it depicts capacitor metallic conducting plate having non-zero thickness.

I am still amazed, that there cannot be 2D metallic conductor or conducting shell with zero thickness having non-zero surface charge density !?

 

[curious_mind]

Although you are in chapter 2 it might be helpful to skim chapter 3. Specifically section 3.2.4 where the method of images for a sphere is covered.

This is the same problem as the one covered in 3.2.4 but inverted so you'll have to make a change of variables but once you do that it will be solved.

Yes I am already familiar with it, but frankly I do not see any applicabilty or even connection of image method with this problem. Is there any ?

 

[kuruman]

I am still amazed, that there cannot be 2D metallic conductor or conducting shell with zero thickness having non-zero surface charge density !?

Who says there cannot be such things? Read this about graphene. The problem is that when you have a 2d material one atomic layer thick, the simple macroscopic model that charge can be uniformly distributed over a surface like a fluid is no longer applicable. One has to consider a quantum mechanical description because, after all, matter is composed of individual atoms.

 

[curious_mind]

Who says there cannot be such things? Read this about graphene. The problem is that when you have a 2d material one atomic layer thick, the simple macroscopic model that charge can be uniformly distributed over a surface like a fluid is no longer applicable. One has to consider a quantum mechanical description because, after all, matter is composed of individual atoms.

No no, I understand there can be lot of things if we consider microscopic view, there will be Quantum Electrodynamics and so on, I understand that. I just want to stick around macroscopic picture for the time being.

But do you mean Graphene is a 2D conductor which can have surface charge induced on it if some charge is put nearby ? Does Graphene show such behavior ? I do not know anything about 2D materials or conductors etc. But this looks interesting to me.

By the way, in 4th edition of Griffiths' "Electrodynamics", in footnote 10, pp. 99, in section 2.5 , it is remarked, in the context of induced charges on the surface of conductors due to point charge placed outside it, that -

10 By the way, the one- and two-dimensional analogs are quite different: The charge on a conducting disk does not all go to the perimeter (R. Friedberg, Am. J. Phys. 61, 1084 (1993)), nor does the charge on a conducting needle go to the ends (D. J. Griffiths and Y. Li, Am. J. Phys. 64, 706 (1996))—see Prob. 2.57.

 

[kuruman]

But do you mean Graphene is a 2D conductor which can have surface charge induced on it if some charge is put nearby ?

All I said is that surface charge density is not a model that works with graphene. You need a quantum mechanical description not an image charge description.

By the way, in 4th edition of Griffiths' "Electrodynamics", in footnote 10, pp. 99, in section 2.5 , it is remarked in the context of induced charges on conductors due to point charge placed outside it.

I have read the Griffiths article in which Griffiths argues (with calculations of course) that if you put some charge on a needle, the charge will not be distributed along the needle with uniform charge density. He had problems modeling the needle. One can imagine an 'infinitely long" linear distribution but a finite segment is quite another story.

Here is a screenshot of the concluding paragraph in Griffiths's article.

 

[hutchphd]

I am very confused by much of this colloquy. Can the OP reference a particular section or equation in Griffiths, please? And

1. I am confused by several f the oanswers. Is the charge at the interior center of a conducting shell???
2. In the limit of zero thickness a dipole layer vanishes (pluses and minusses add to zero) There may be a residual net charge.

I am quite mystified by this entire thread. Please may we clean it up.

 

[haruspex]

What if we take thickness of the shell to be zero. An ideal situaiton

The only safe way to handle idealisations is to start with a realistic version then take the limit as the idealisation is approached.
Treating the shell as having an inner and outer surface, the distribution on the inner surface will always be such as to neutralise the field from the internal charge.
This results in there being no field within material of the shell.
The charges pushed to the outer surface will therefore distribute evenly.
Since this is independent of the shell thickness, this arrangement will also apply in the limit.

 

[kuruman]

Since this is independent of the shell thickness, this arrangement will also apply in the limit.

That works. In the limit that the inner radius of the shell is equal to the outer radius, then we have a shell of zero thickness which means "no shell at all" in which case the potential and electric field everywhere in space will be that of the point charge. OP seems to think that in the limit, there can be a conducting shell with only one surface

What if we take thickness of the shell to be zero. An ideal situaiton where hollow sphere only has one surface.

 

[kuruman]

I am very confused by much of this colloquy. Can the OP reference a particular section or equation in Griffiths, please? And

1. I am confused by several f the oanswers. Is the charge at the interior center of a conducting shell???
2. In the limit of zero thickness a dipole layer vanishes (pluses and minusses add to zero) There may be a residual net charge.

I am quite mystified by this entire thread. Please may we clean it up.

I think that OP's question was adequately answered in post #2. In my opinion it lost its focus because of OP's whataboutism.

 

[haruspex]

That works. In the limit that the inner radius of the shell is equal to the outer radius, then we have a shell of zero thickness which means "no shell at all" in which case the potential and electric field everywhere in space will be that of the point charge.

No, the external field is different. The effect of the sphere is to make the point charge appear to be at the centre of the sphere.

 

[haruspex]

I am very confused by much of this colloquy. Can the OP reference a particular section or equation in Griffiths, please? And

1. I am confused by several f the oanswers. Is the charge at the interior center of a conducting shell???
2. In the limit of zero thickness a dipole layer vanishes (pluses and minusses add to zero) There may be a residual net charge.

I am quite mystified by this entire thread. Please may we clean it up.

I think that OP's question was adequately answered in post #2. In my opinion it lost its focus because of OP's whataboutism.

That's not how I read the thread.
In post #3, @curious_mind clarified that the puzzlement concerned a zero thickness conducting shell. If having no net charge, how can it affect the field from the point charge (which is not at the centre of the sphere)?
The answer is to take the idealisation of zero thickness as a limiting value. Since for all nonzero thicknesses the external field becomes recentred on the centre of the sphere, that should be taken as the result also in the idealisation.