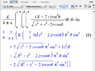pence
- 3
- 0
~Electrodynamics~ Potential from charged sphere. I am lost :/
A sphere of radius R, centered at the origin, carries a charge density ρ(r,θ)=κ/r^2(R-2r)sin^2(θ).
κ is constant. Find exact potential.
1/4∏ε∫ρ∂t/r
Question and attempt via attachments :)
I do not think my solution is correct please help!
Thanks all for looking!
Homework Statement
A sphere of radius R, centered at the origin, carries a charge density ρ(r,θ)=κ/r^2(R-2r)sin^2(θ).
κ is constant. Find exact potential.
Homework Equations
1/4∏ε∫ρ∂t/r
The Attempt at a Solution
Question and attempt via attachments :)
I do not think my solution is correct please help!
Thanks all for looking!