Em waves and magnetic field lines

Thread starter physics user1
Start date Nov 20, 2016
Tags

Em Em waves Field Field lines Lines Magnetic Magnetic field Magnetic field lines Waves

AI Thread Summary

Magnetic field lines in electromagnetic waves are closed loops, which can be difficult to visualize. The discussion centers around understanding how these closed lines function within the context of an electromagnetic wave. A standard dipole antenna is referenced as a common example to illustrate the radiation pattern associated with these waves. The presence of the antenna is confirmed as central to the wave's structure. This explanation helps clarify the relationship between magnetic field lines and electromagnetic radiation.

Nov 20, 2016

physics user1

So i know that magnetic field lines are closed, in an electromagnetc wave how can be these lines closed? i cannot picture this in my head

Physics news on Phys.org

Nov 20, 2016

Drakkith

Mentor

I believe they look something like the following:

Nov 20, 2016

physics user1

Thanks @Drakkith

Dec 12, 2016

cpxuvs

Drakkith said:

I believe they look something like the following:

Is an antenna in the middle?

Dec 12, 2016

Drakkith

Mentor

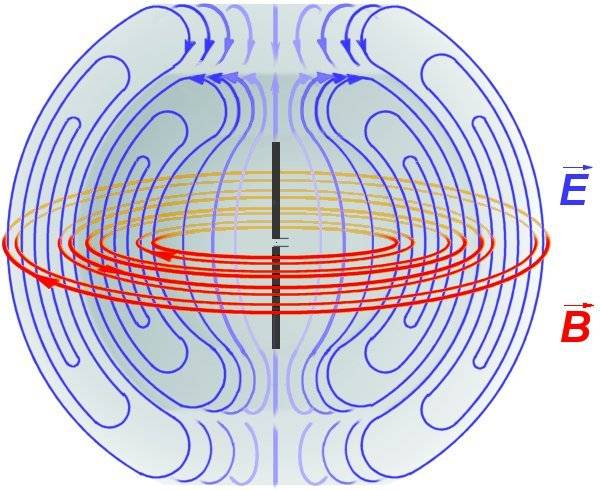
cpxuvs said:

Is an antenna in the middle?

Yes there is. I believe that's the radiation pattern of a standard dipole antenna.

Thread 'Paradox of Superconductivity'

For a series R-L circuit that uses superconductive components, how long would it take for current to build up after the power is turned on?

View full post »

Thread 'How to picture the vector potential?'

Susskind (in The Theoretical Minimum, volume 1, pages 203-205) writes the Lagrangian for the magnetic field as ##L=\frac m 2(\dot x^2+\dot y^2 + \dot z^2)+ \frac e c (\dot x A_x +\dot y A_y +\dot z A_z)## and then calculates ##\dot p_x =ma_x + \frac e c \frac d {dt} A_x=ma_x + \frac e c(\frac {\partial A_x} {\partial x}\dot x + \frac {\partial A_x} {\partial y}\dot y + \frac {\partial A_x} {\partial z}\dot z)##. I have problems with the last step. I might have written ##\frac {dA_x} {dt}...

View full post »

Thread 'Griffith, Electrodynamics, 4th Edition, Example 4.8. (Second part)'

I am reading the Griffith, Electrodynamics book, 4th edition, Example 4.8. I want to understand some issues more correctly. It's a little bit difficult to understand now. > Example 4.8. Suppose the entire region below the plane ##z=0## in Fig. 4.28 is filled with uniform linear dielectric material of susceptibility ##\chi_e##. Calculate the force on a point charge ##q## situated a distance ##d## above the origin. In the page 196, in the first paragraph, the author argues as follows ...

View full post »