- #141
metastable
- 514
- 53
The equations seem to give absurd results with very high passenger vehicle masses:
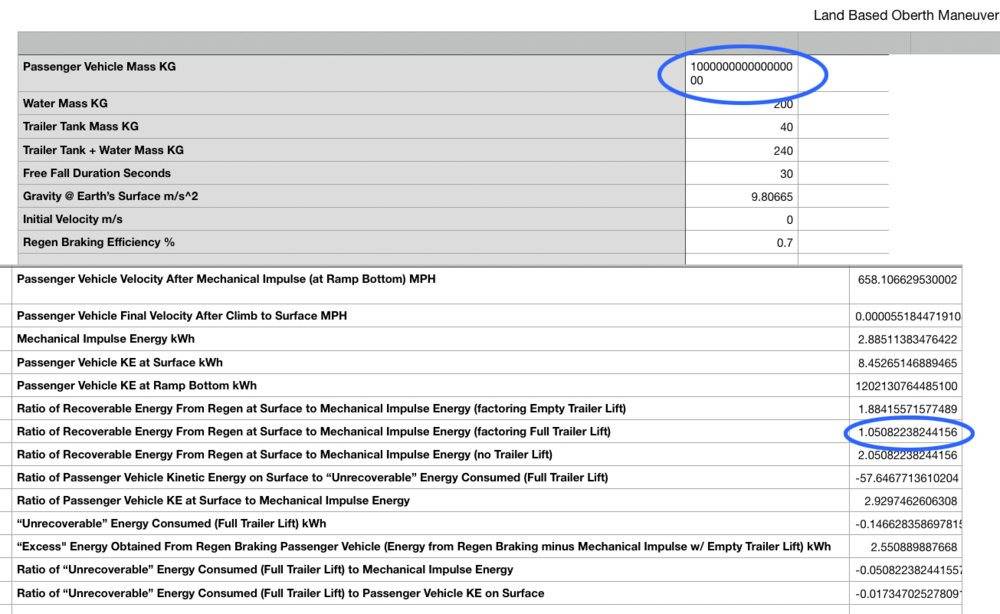
Dale said:Excel code is almost impossible to debug.
metastable said:First I will share an example of the equations I would use to calculate the power consumption of a given standard land vehicle at a given speed in a given set of conditions.
sysprog said:The ACME Corporation cannot guarantee the safety of a rider aboard an electric skateboard operated at a speed exceeding 100 mph100 mph100\ mph.
Please sign your organ donor card before riding that thing, kid; how do you deal with the snap (aka jounce)? Oh, and, I have a friend whose pet kitty needs a cornea transplant. On a slightly more technical note, umm -- WB cartoon speed was measured in frames per second (12 fps doubled to 24); not really mph -- Mr. Coyote's speed is forever less than that of the Road Runner, speed in this instance being considered as the derivative of distance with respect to time -- the reasoning behind the standard for the time required to complete 1 frame (not for the artist; for the viewer) is hinted at by the following inequality constraint: ##1(frametime) < 1(blinkofaneye)##. Actually, it has more to do with human brain visual image processing time -- the frame rate is determined by how many frames per second are required to cause the visual system to report continuous movement instead of separate still images.metastable said:for comparison I will share a photo of, what I personally consider, a "standard car"-- quite literally the drivetrain of the fastest electric skateboard in the world, capable of 70+ ##mph##:
View attachment 246979
sysprog said:@metastable posted me, and I mostly begged off for now, regarding his to-me-somewhat-quizzical spreadsheet code. My at-a-glance response was that the source of the problem may/might be in his having exhausted the capacity of the sqrt function.
Please disambiguate the last-line expression -- in particular, the '/2' -- does that fractionate the entirety? -- it's ok to use ##\frac 1 2## and/or extra parens (instead of making me have to go with PEMDAS and the rest of my feeble memory of the order of operations) to keep it clear what you mean ##\dots##metastable said:For me, the most interesting part of the whole exercise was determining the formula for calculating how many Joules of Mechanical Impulse between the vehicle and the trailer will bring the trailer to a complete halt at the bottom of the ramp every time, depending on the Trailer Mass, Vehicle Mass, Free Fall Duration, Initial Velocity Before Free Fall, and the Gravitational Acceleration at Earth's Surface:
##W_i## = ##12.8*10^6## = Mechanical Impulse Energy (##Joules##) That Brings Trailer to 0 Velocity At Ramp Bottom
##M_t## = ##240## = Trailer Tank + Water Mass (##Kilograms##)
##M_v## = ##10^3## = Passenger Vehicle Mass (##Kilograms##)
##T_d## = ##30## = Free Fall Duration (##Seconds##)
##V_i## = ##0## = Initial Velocity Before Free Fall (##m/s##)
##G_e## = ##9.80## = Gravity Acceleration at Earth’s Surface (##m/s^2##)
##W_i=M_tV_iT_dG_e+(M_tT_d^2G_e^2+M_tV_i^2)/2+(M_t^2(V_i+T_dG_e)^2)/(2M_v)##
I'm not sure what you mean exactly, does this help?sysprog said:Please disambiguate the last-line expression -- in particular, the '/2' -- does that fractionate the entirety? -- it's ok to use 1212\frac 1 2 and/or extra parens (instead of making me have to go with PEMDAS and the rest of my feeble memory of the order of operations) to keep it clear what you mean
Let me be certain that my understanding is clear. We are talking about a trailer full of water behind a passenger vehicle. The water is not ejected in this scenario. It remains with the trailer throughout. There are no frictional losses. The whole assembly drops and gains kinetic energy. The passenger vehicle is then ejected at a velocity such that conservation of momentum brings the trailer to a stop.metastable said:##W_i=M_tV_iT_dG_e+(M_tT_d^2G_e^2+M_tV_i^2)/2+(M_t^2(V_i+T_dG_e)^2)/(2M_v)##
^I haven't gone through your whole analysis yet but I had a question about this line... shouldn't it be:jbriggs444 said:##M_{tot}V_b=M_vV_v##
No. It was correct as written. Momentum before = momentum after. The momentum before is the total mass times the velocity of the complete assembly.metastable said:^I haven't gone through your whole analysis yet but I had a question about this line... shouldn't it be:
##M_{trailer}V_b=M_vV_v##
As I understand this, you want ##V_b## to be the forward velocity of the trailer+vehicle assembly.metastable said:Effectively what I used was this:
##m_1v_1=m_2v_2##
^If the mass of the trailer acquires the ramp-bottom velocity in an energetic interaction / push-off with the passenger section (bringing the trailer to a halt), then the passenger vehicle velocity is ##v_2## + ##V_{bottom}##
The energy of the interaction between trailer and tank would be:
##W_i=(1/2)m_1V_b^2+(1/2)m_2(v_2+V_b)^2##
Was it wrong?
metastable said:##W_i## = ##12.8∗10^6## = Mechanical Impulse Energy (##Joules##) That Brings Trailer to 0 Velocity At Ramp Bottom
##M_t## = ##240## = Trailer Tank + Water Mass (##Kilograms##)
##M_v## = ##10^3## = Passenger Vehicle Mass (##Kilograms##)
##T_d## = ##30## = Free Fall Duration (##Seconds##)
##V_i## = ##0## = Initial Velocity Before Free Fall (##m/s##)
##G_e## = ##9.80## = Gravity Acceleration at Earth’s Surface (##m/s^2##)
I am not willing to run the numbers if you are not willing to do the algebra.metastable said:^Using your separate method do you calculate the same value for ##W_i##? The reason I ask is I don't understand part of your method at the beginning.
metastable said:Effectively what I used was this:
##m_1v_1=m_2v_2##
^If the mass of the trailer acquires the ramp-bottom velocity in an energetic interaction / push-off with the passenger section (bringing the trailer to a halt), then the passenger vehicle velocity is v2v2v_2 + VbottomVbottomV_{bottom}
The energy of the interaction between trailer and passenger section would be:
##W_i=(1/2)m_1V_b^2+(1/2)m_2(v_2+V_b)^2##
Was it wrong?
Yes. As I explained, you need to pick a frame of reference for your energy balance.metastable said:In my above calculation, ##v_2## was intended to be the velocity of the passenger section, relative to the ##V_{bottom}## rest frame of the trailer+vehicle at the bottom of the tunnel before the push off, so ##v_2 + V_{bottom}## is the final velocity of the passenger vehicle while still on the flat section at the bottom of the tunnel.
metastable said:The energy of the interaction between trailer and passenger section would be:
##W_i=(1/2)m_1V_b^2+(1/2)m_2(v_2+V_b)^2##
Was it wrong?
Yes, that would be a correct calculation for incremental work done.metastable said:I misspoke here, I meant:
##W_i=(1/2)m_1V_b^2+(1/2)m_2(v_2)^2##
Thanks for that.metastable said:bringing all the equations together, we have:
##m_1v_1=m_2v_2##
##v_2=(m_{trailer}V_{bottom})/m_{passenger}##
##W_i=(1/2)m_{trailer}V_{bottom}^2+(1/2)m_{passenger}(v_2)^2##
##V_{passenger}=v_2+V_{bottom}##
##W_{KEpassenger}=(1/2)m_{passenger}(v_2+V_{bottom})^2##
metastable said:bringing all the equations together, we have:
##m_1v_1=m_2v_2##
##v_2=(m_{trailer}V_{bottom})/m_{passenger}##
##W_i=(1/2)m_{trailer}V_{bottom}^2+(1/2)m_{passenger}(v_2)^2##
I don’t believe so because when I input it in a calculator it looks like this:sysprog said:?