Jazoar
- 1
- 0
Hi All,
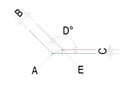
I need help to find an equation that will give me the location of 'E' in the image below.
'A' is the starting point on a graph.
All values from 'B' to 'D' are known values.
Currently, 'B' = 50, 'C' = 20, & 'D' = 135° - but I need an equation that will find 'E' no matter what these values are.
View attachment 7931
Any help would be greatly appreciated!
- Jazoar
I need help to find an equation that will give me the location of 'E' in the image below.
'A' is the starting point on a graph.
All values from 'B' to 'D' are known values.
Currently, 'B' = 50, 'C' = 20, & 'D' = 135° - but I need an equation that will find 'E' no matter what these values are.
View attachment 7931
Any help would be greatly appreciated!
- Jazoar