Equilibrium of a rigid solid on a rod

[Guillem_dlc]

Homework Statement

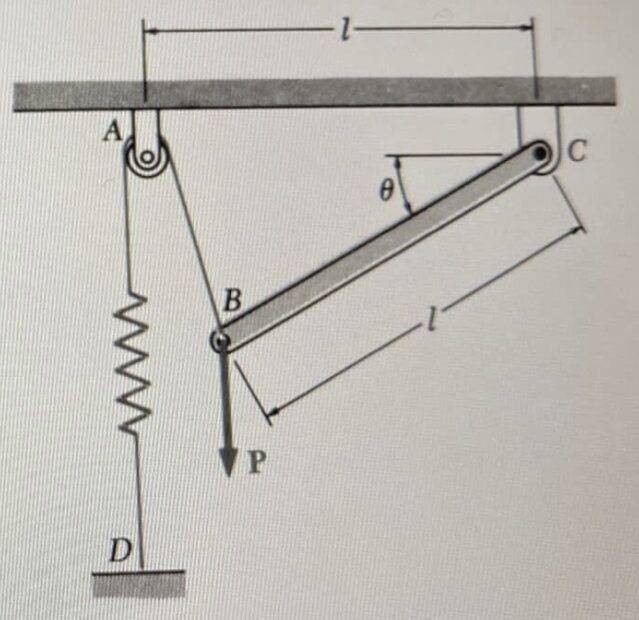
At the end $B$ of rod $BC$ a vertical load $P$ is applied. The spring constant is $k$ and it forms an angle $\theta=0$ when the spring is unstretched.

a) Neglecting the weight of the rod, express the angle $\theta$ corresponding to the equilibrium position in terms of $P$, $k$ and $l$. Sol: $\theta =\arctan \dfrac{P}{kl}$

b) Determine the value of $\theta$ corresponding to equilibrium if $P=2kl$. Sol: $\theta =63,4\, \textrm{º}$

Relevant Equations

$F=k\Delta x$, $\sum M_C=0$

Figure:

Attempt at a Solution:
$$F=k\Delta x=lk\sin \theta$$
$$\delta x=0 \quad \textrm{when} \theta=0$$

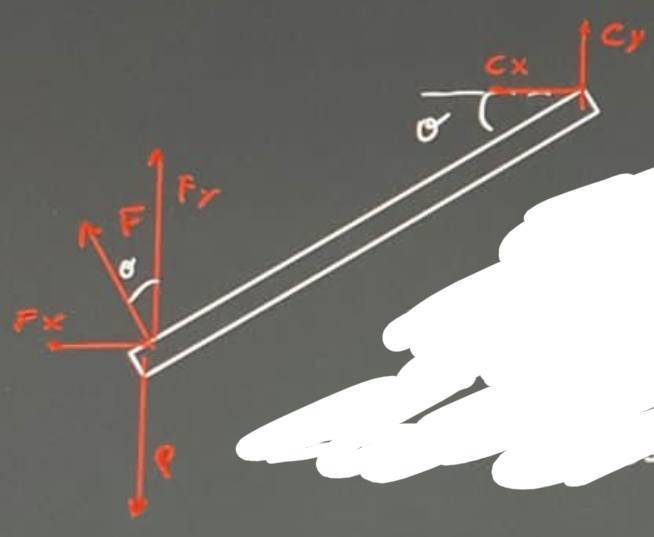
$$\sum M_C=0\rightarrow$$
$$\rightarrow Pl\cos \theta -F_yl\cos \theta -F_xl\sin \theta =0\rightarrow$$
$$\rightarrow Pl\cos \theta -Fl\cos^2 \theta -Fl\sin^2 \theta=0\rightarrow$$
$$\rightarrow Pl\cos \theta -kl^2\sin \theta \cos^2 \theta -kl^2\sin^2 \theta =0\rightarrow$$
$$P\cos \theta =kl\sin \theta \cos^2 \theta -kl\sin^3 \theta =0\rightarrow$$
$$\dfrac{P}{kl}=\dfrac{\sin \theta \cos^2 \theta -\sin^3 \theta}{\cos \theta}\rightarrow \dfrac{P}{kl}=\tan \theta \dfrac{\cos^2 \theta -\sin^2 \theta}{\cos \theta}\rightarrow$$
$$\rightarrow \dfrac{P}{kl}=\dfrac{(\cos \theta +\sin \theta)(\cos \theta -\sin \theta)}{\cos \theta}\tan \theta =(1-\tan^2 \theta)\tan \theta$$
because
$$\left( \dfrac{\cos \theta}{\cos \theta}+\dfrac{\sin \theta}{\cos \theta}\right) \cdot \left( \dfrac{\cos \theta}{\cos \theta}-\dfrac{\sin \theta}{\cos \theta}\right) =(1+\tan)\cdot (1-\tan)=$$
$$=1-\tan +\tan -\tan^2 =1-\tan^2 \theta$$
I've tried this but I don't know

 

[jbriggs444]

As I understand it, you have assumed that the support force ($\vec{F}$) from the spring is applied at an angle of $\theta$ from the vertical. This means that $\vec{F}$ will be at right angles to the rod.

Can you justify that assumption?

 

[Guillem_dlc]

As I understand it, you have assumed that the support force ($\vec{F}$) from the spring is applied at an angle of $\theta$ from the vertical. This means that $\vec{F}$ will be at right angles to the rod.

Can you justify that assumption?

Yes, isn't it?

 

[erobz]

Yes, isn't it?

The length of the bar is $l$, the horizontal distance between supports is also $l$. Try to form that "right triangle", you will notice something suspicious.

Also: It should be stated we are to neglect the size of the pulley.

 

[haruspex]

Yes, isn't it?

It often helps to consider extreme cases. Sketch the diagram with $\theta=90°$.

 

[Guillem_dlc]

The length of the bar is $l$, the horizontal distance between supports is also $l$. Try to form that "right triangle", you will notice something suspicious.

Also: It should be stated we are to neglect the size of the pulley.

I don't quite understand what you mean

 

[erobz]

I don't quite understand what you mean

What does the Pythagorean Theorem say about the lengths of sides in "right" triangles? Try applying it to triangle $ABC$.

 

[jbriggs444]

I don't quite understand what you mean

The pulley size remark? Or the isosceles triangle part?

 

[kuruman]

Homework Statement:: At the end $B$ of rod $BC$ a vertical load $P$ is applied. The spring constant is $k$ and it forms an angle $\theta=0$ when the spring is unstretched.

When the spring is unstretched and $\theta = 0$, points A and B are coincident (assuming that $l$ is much greater than the pulley radius). As the spring is stretched under the load, point $B$ describes a circle of radius $l$. Triangle ACB is isosceles ($AC=BC$). What is length $AB$ in terms of $\theta$? By how much does the spring stretch?

 

[Guillem_dlc]

Ok now I'll try again