Experimental Physics Challenge, June 2021

[Twigg]

Trying this out for fun, and seeing if people find this stimulating or not. Feedback appreciated! There's only 3 problems, but I hope you'll get a kick out of them. Have fun!1. Springey Thingies:

Two damped, unforced springs are weakly coupled and obey the following equations of motion: $$\ddot{x}_a +\gamma \dot{x}_a + \omega_{0,a}^2 x_a + \beta^2 (x_b - x_a) = 0$$ $$\ddot{x}_b +\gamma \dot{x}_b + \omega_{0,b}^2 x_b - \beta^2 (x_b - x_a) = 0$$ You wish to measure the difference between the two springs' natural (undamped) resonant frequencies: $\Delta = \omega_{0,b} - \omega_{0,a}$. Your measurement will be complicated by the coupling coefficient β and the damping coefficient γ. Design a simple procedure for measuring $\Delta$.

Assume for simplicity that $\omega_0 = \frac{1}{2}\left(\omega_{0,b} + \omega_{0,a}\right) = 1\mathrm{kHz}$ and $\gamma = 125\mathrm{s^{-1}}$ are known exactly. You are also given that Δ is of order $2\pi\times 1\mathrm{mHz}$ and β is of order $2\pi\times100\mathrm{mHz}$. The uncertainty in either spring's measured position is determined by the spring's initial conditions by $$\sigma_x = \left(2.6\times10^{-7}\right)\sqrt{x(0)^2 + \frac{\dot{x}(0)^2}{\omega_0^2 - \gamma^2 / 4}}$$
Your answer should include a set of times at which to measure the spring positions $x_a$ and $x_b$, a formula for $\Delta$ in terms of these measurements, and a standard deviation on the value of $\Delta$. Optimal answers should have uncertainty $\sigma_\Delta \approx 2\pi \times 10\mathrm{\mu Hz}$ with as little as two position measurements. Numerical and analytical methods are accepted so long as the results are valid!2. "Honey, I shrunk the error bars!"

You and your coworker Bob are studying a chemical reaction $A + B \leftrightarrow C$. For this study, you vary the temperature of the mixture and record the concentration of species C: $$x = \frac{N_C}{N_A + N_B + N_C}$$ where $N_A$, $N_B$, and $N_C$ refer to the total number of each species A, B, and C respectively. For each temperature setting, you record a number (M) of measurements of $N_A$, $N_B$, $N_C$ (M measurements of each). Furthermore, you know that $N_A$, $N_B$, and $N_C$ are all Poisson distributed. You then calculate an average $\mathrm{E}[x]$ and standard error $\sigma_{\mathrm{E}[x]}$ for each set of measurements. Up to this point, everything makes sense.

Your coworker Bob comes up with a wacky idea. Bob re-defines the concentration (now called $x'$) within a set of M measurements as follows: $$x'_i = \frac{N_{C,i}}{\mathrm{E}[N_A] + \mathrm{E}[N_B] + N_{C,i}} \; \; \mathrm{for} \; i=1,2,...,M$$ Bob argues that taking expectation values over $N_A$ and $N_B$ in the denominator eliminates extraneous noise. What's more, Bob has a mathematical proof that shows that $\mathrm{Var}[x']\leq\mathrm{Var}[x]$. You make a bet with Bob: you collect 100 data sets, each consisting of M measurements, and compare the estimated standard error on the mean $\sqrt{\frac{1}{M}\mathrm{Var}[x']}$ (aka the "error bars" on the mean of each set of M measurements) with the observed standard deviation on the means of each of the 100 sets of measurements $\sigma_{\mathrm{E}[x']}$. The data shows that $\sigma_{\mathrm{E}[x']} > \sqrt{\frac{1}{M}\mathrm{Var}[x']}$, and more specifically that $${\sigma_{\mathrm{E}[x']}}=\sigma_{\mathrm{E}[x]}$$ This last result can be interpreted to mean there is no free lunch for Bob. Reproduce Bob's proof that $\mathrm{Var}[x']\leq\mathrm{Var}[x]$ and prove the "no free lunch" result $\sigma_{\mathrm{E}[x']}=\sigma_{\mathrm{E}[x]}$.3. Pink, pink, you stink!

Consider the following bridge circuit, where the variable resistor sees "pink" noise (aka 1/f noise):

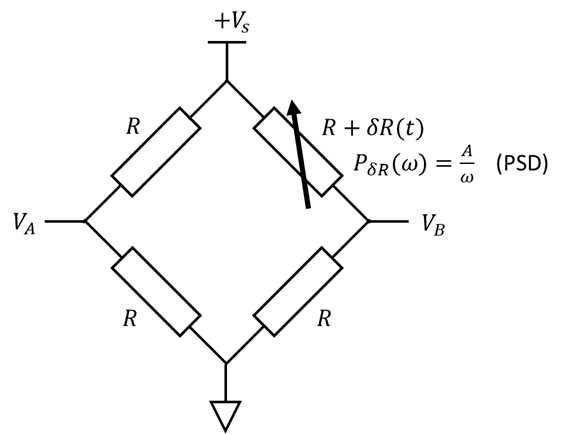
All 4 resistors have identical resistance on average, but the top right resistor fluctuates with a pink spectrum: $$P_{\delta R}(\omega) = \frac{A}{\omega}$$ where $P_x(\omega)$ is the power spectral density (PSD) of the function $x(t)$. Each resistor also puts out thermal noise (Johnson-Nyquist noise). Find an expression in terms of the measured voltages $V_A$, $V_B$, and $V_S$ that is proportional to the fluctuating resistance $\delta R$ but is independent of thermal noise.

Some sample data is attached (filename is “pinkdatafinalfinal.csv”), where each voltage ($V_A$,$V_B$, and $V_S$) is reported versus time in a CSV format. Extract the constant A as defined above and state your uncertainty on A, given $R = 1\mathrm{\Omega}$. My solution has uncertainty on the order of $1 \times 10^{-8} \mathrm{\mathrm{\Omega^2}}$. There are many methods for tackling this problem and some give higher precision than others.

 

[Dale]

Thanks for hosting it this month @Twigg

Anyone who would like to host a future month, just let me know by private message

 

[Greg Bernhardt]

Bumping this challenge! Too tough for everyone?

 

[Twigg]

I probably went a little overboard with the length and complexity of each problem Here are some hints if y'all are still interested!

Spoiler: Problem 1

The most efficient way to do this problem is to write a quick and dirty numerical program to directly integrate these equations of motion and play around with it. I did this with scipy's odeint function (attached below for all to use). Play around by plotting some different linear combinations of $x_a$ and $x_b$ for different initial conditions, and you'll start to see something magical happening! At that point, you'll know what to look for in the analysis.

from scipy.integrate import odeint
import numpy as np
import matplotlib.pyplot as plt

# Define physical constants
w0 = 2*np.pi*1000 #average resonant frequency (omega_0) in radians per second
g = 125 #damping rate (gamma) in inverse seconds
B = 2*np.pi*0.5 #coupling rate (beta) in radians per second
D = 2*2*np.pi*4E-3 #difference in resonant frequencyes (Delta) in radians per second

w0a = w0-0.5*D #resonant frequency of the first spring
w0b = w0+0.5*D #resonant frequency of the second spring

def odes(x,t): #return first derivatives in time of the positions and velocities of each spring
  dxdt0 = -(g*x[0] + (w0a**2 - B**2)*x[2] + (B**2)*x[3]) #calculate acceleration of the first spring
  dxdt1 = -(g*x[1] + (w0b**2 - B**2)*x[3] + (B**2)*x[2]) #calculate acceleration of the second spring
  dxdt2 = x[0] #calculate velocity of the first spring
  dxdt3 = x[1] #calculate velocity of the second spring
  return [dxdt0,dxdt1,dxdt2,dxdt3]

x0 = [0,0,1,0] #initial condition of the two springs in the following format:
#x0[0] is the velocity of the first spring in meters per second
#x0[1] is the velocity of the second spring in meters per second
#x0[2] is the position of the first spring in meters
#x0[3] is the position of the third spring in meters

# declare a time vector
num_samples = 200 #resolution of the time vector
t = np.linspace(0,2/g,2*num_samples) #create the time vector in seconds, out to 2 decay times as an example

#Integrate!
x = odeint(odes,x0,t)

#Make some plots
fig, axes = plt.subplots(1,2)

ax1 = axes[0]
ax2 = axes[1]

ax1.plot(t,x[:,2])
ax2.plot(t,x[:,3])
ax1.set_xlabel('Time (s)')
ax2.set_xlabel('Time (s)')
ax1.set_ylabel('x_a (m)')
ax2.set_ylabel('x_b (m)')

Spoiler: Problem 2

The starting point here is to express each numeric variable as $N = \mathrm{E}[N] + \delta N$ where $\delta N$ represents fluctuations around the mean. Then you'll want to series expand x and/or x' to first order (since the quantities are Poisson distributed, you know that $\frac{\sigma_N}{N} = \frac{1}{\sqrt{N}}$, and since this is chemistry-based you can expect $N$ to be ginormous, so there's no harm in truncating to first order).

Spoiler: Problem 3

Any circuit analysis of your favorite variety (kirchoff, nodal, mesh, whatever) will reveal that even the thermal noise on the voltages $V_A$, $V_B$, and $V_S$ are correlated. A little strategy and a quick first order series expansion will show that there is a simple function of these voltages that is independent of noise and scales like $C\delta R + O(\delta R^2)$ for some constant C.

 

[Twigg]

Been a week, so I thought I might do a second round of hints

Spoiler: Problem 1

Try the initial condition $x_a(0) = x_b(0) = 1$ and plot the difference in positions $x_b(t) - x_a(t)$. Notice any patterns? Try changing the value of $\Delta$ in the simulation and seeing how that plot changes. Since you know the damping rate $\gamma$ exactly, you can even look at the quantity $e^{+\gamma t} (x_b(t) - x_a(t))$ to see the effect minus damping without introducing any error.

Spoiler: Problem 2

Notice that when calculating the variance $\mathrm{Var}[x']$ within a set of M measurements, the mean values $\mathrm{E}[N_A]$ and $\mathrm{E}[N_B]$ are constants, but when comparing multiple sets of M measurements these expectation values are random variables with uncertainty given by the standard deviations $\sigma_{\mathrm{E}[N_A]}$ and $\sigma_{\mathrm{E}[N_B]}$ respectively.

Spoiler: Problem 3

Try looking at the difference $V_A - V_B$, and taking a first order series expansion in $\delta R$. This quantity still has thermal noise multiplied in, but there's a way to get rid of it using $V_S$. To do the spectral density estimate, a Welch periodogram is your best bet. From there, it's just a matter of regression using whatever numerical method you like.

 

[ergospherical]

Write $N = \mathbb{E}[N] + \delta N$\begin{align*}

x &= \dfrac{N_C}{N_A + N_B + N_C} \\ \\
&= \dfrac{\mathbb{E}[N_C] + \delta N_C}{\mathbb{E}[N_A] + \mathbb{E}[N_B] + \mathbb{E}[N_C] + \delta N_A + \delta N_B + \delta N_C} \\ \\
&= \dfrac{\mathbb{E}[N_C] + \delta N_C}{\mathbb{E}[N_A] + \mathbb{E}[N_B] + \mathbb{E}[N_C]} \left( 1 - \dfrac{\delta N_A + \delta N_B + \delta N_C}{\mathbb{E}[N_A] + \mathbb{E}[N_B] + \mathbb{E}[N_C]} + \dots \right)

\end{align*}Denoting $N_{\tau} = N_{A} + N_{B} + N_{C}$ and identifying $\mathbb{E}[x] = \frac{\mathbb{E}[N_C]}{\mathbb{E}[N_{\tau}]}$\begin{align*}

x &= \frac{\mathbb{E}[N_C]}{\mathbb{E}[N_{\tau}]} + \frac{\delta N_C}{\mathbb{E}[N_{\tau}]} - \frac{\mathbb{E}[N_C]}{\mathbb{E}[N_{\tau}]} \frac{\delta N_A + \delta N_B + \delta N_C}{\mathbb{E}[N_{\tau}]} \\

&= \mathbb{E}[x] + \left(1 - \mathbb{E}[x] \right) \frac{\delta N_C}{\mathbb{E}[N_{\tau}]} - \mathbb{E}[x] \left( \frac{\delta N_A + \delta N_B}{\mathbb{E}[N_{\tau}]} \right) \\ \\

\implies \mathbb{V}[x] &= \frac{\left(1-\mathbb{E}[x] \right)^2}{\mathbb{E}[N_{\tau}]^2} \mathbb{V}[N_C] + \frac{\mathbb{E}[x]^2}{\mathbb{E}[N_{\tau}]^2}\left(\mathbb{V}[N_A] + \mathbb{V}[N_B] \right)

\end{align*}Now for $x'$\begin{align*}

x' &= \dfrac{1}{M} \sum_{i=1}^M x_i' \\
&= \dfrac{1}{M} \sum_{i=1}^M \dfrac{\mathbb{E}[N_{C,i}] + \delta N_{C,i}}{\mathbb{E}[N_A] + \mathbb{E}[N_B] + \mathbb{E}[N_{C,i}]} \left( 1 - \dfrac{\delta N_{C,i}}{\mathbb{E}[N_A] + \mathbb{E}[N_B] + \mathbb{E}[N_{C,i}]} + \dots \right) \\
&= \dfrac{1}{M} \sum_{i=1}^M \dfrac{\mathbb{E}[N_C]}{\mathbb{E}[N_\tau]} + \dfrac{\delta N_C}{\mathbb{E}[N_{\tau}]} - \dfrac{\mathbb{E}[N_C] \delta N_C}{\mathbb{E}[N_{\tau}]^2} + \dots \\
&= \dfrac{1}{M} \sum_{i=1}^M \dfrac{\mathbb{E}[\mathbb{E}[N_C]] + \delta \mathbb{E}[N_C]}{\mathbb{E}[\mathbb{E}[N_\tau]] + \delta \mathbb{E}[N_{\tau}]} + \dfrac{\delta N_C}{\mathbb{E}[\mathbb{E}[N_{\tau}]] + \delta \mathbb{E}[N_{\tau}]} + \dots \\
&= \dfrac{1}{M} \sum_{i=1}^M \dfrac{\mathbb{E}[\mathbb{E}[N_C]] + \delta \mathbb{E}[N_C] + \delta N_C}{\mathbb{E}[\mathbb{E}[N_\tau]]} \left(1 - \dfrac{\delta \mathbb{E}[N_{\tau}]}{\mathbb{E}[\mathbb{E}[N_\tau]]} \right) + \dots\end{align*}Then identifying $\mathbb{E}[x'] = \dfrac{\mathbb{E}[\mathbb{E}[N_C]]}{\mathbb{E}[\mathbb{E}[N_{\tau}]]}$\begin{align*}

x' &= \dfrac{1}{M} \sum_{i=1}^M \mathbb{E}[x'] + (1- \mathbb{E}[x']) \dfrac{\delta \mathbb{E}[N_C]}{\mathbb{E}[\mathbb{E}[N_{\tau}]]} - \mathbb{E}[x'] \left( \dfrac{\delta \mathbb{E}[N_A] + \delta \mathbb{E}[N_B]}{\mathbb{E}[\mathbb{E}[N_{\tau}]]} \right) + \dots \\
\mathbb{V}[x'] &= \dfrac{1}{M} \sum_{i=1}^M \dfrac{(1- \mathbb{E}[x'])^2}{\mathbb{E}[\mathbb{E}[N_{\tau}]]^2 } \mathbb{V}[\mathbb{E}[N_C]] + \dfrac{ \mathbb{E}[x']}{\mathbb{E}[\mathbb{E}[N_{\tau}]]^2} \left( \mathbb{V}[\mathbb{E}[N_A]] + \mathbb{V}[\mathbb{E}[N_B]] \right) + \dots\end{align*}Hence there is no free lunch, $\mathbb{V}[\mathbb{E}[x]] = \mathbb{V}[\mathbb{E}[x']]$. Bob incorrectly assumed that the $\mathbb{E}[N]$ were constant when evaluating $x'$ (as opposed to random variables) and erroneously concluded that $\mathbb{V}[x'] = \dfrac{1}{M} \sum_{i=1}^M \dfrac{(1- \mathbb{E}[x'])^2}{\mathbb{E}[\mathbb{E}[N_{\tau}]]^2 } \mathbb{V}[\mathbb{E}[N_C]]$.

 

[Twigg]

Just wanted to share a little commentary on problem 2, which @ergospherical solved nicely. This problem was inspired by a real dilemma that occurred in my research experience. One of the first things we all learn in statistics is that the standard error on the mean is the standard deviation divided by sqrt(N). This problem stuck in my mind because it violates that elementary rule. If you estimate the standard error on the mean of x' using the standard deviation on x', assuming Poissonian statistics on all the N's, you would see a $\chi^2$ as high as 12ish in your data (observed error / estimated error). The bottom line here is that unless you introduce new data, or exploit an existing correlation, you can't reduce your error, informally speaking.

 

[Twigg]

Releasing these solutions one at a time, as they're lengthy and I don't want to lose my work by accident.

Here's Problem 1

Spoiler: Problem 1

Since this is a coupled spring problem, the first step is to think about normal modes. There are two of them in this problem. They can be solved analytically, but you get more insight by taking series approximations (first order in $\Delta$, and second order in $\beta$). To get the normal mode frequencies, first take a Laplace transform of the equations of motion, and write it as a matrix:
$$\left( \begin{array}{cc} s^2 + \gamma s + (\omega_0 - \frac{\Delta}{2})^2 - \beta^2 & \beta^2 \\ \beta^2 & s^2 + \gamma s + (\omega_0 + \frac{\Delta}{2})^2 \\ \end{array} \right) \left( \begin{array}{cc} X_a(s) \\ X_b(s) \end{array} \right) = 0$$ For this to hold for any value of the Laplace transform vector, the matrix must have determinant equal to 0 at the natural frequencies of oscillation (i.e., the normal modes). You can solve for the normal modes analytically, or you can do it on paper more easily by dropping higher order terms carefully. Solving analytically and splitting s into real and imaginary parts $s = \sigma \pm i \omega$, you get $$\omega = \sqrt{\omega_1^2 - \beta^2 + \left( \frac{\Delta}{2} \right)^2 \pm \sqrt{\beta^4 + \Delta^2 \omega_0 ^2}}$$ where $\omega_1 = \sqrt{\omega_0^2 - \gamma^2 / 4}$ is the damped resonance frequency for a single spring. Expanding the expression for the normal mode frequencies, $$\omega_{\pm} \approx \omega_1 - \frac{\beta^2}{2\omega_1} + \frac{\Delta^2}{8 \omega_1} \pm \frac{\sqrt{\beta^4 + \Delta^2 \omega_0 ^2}}{2\omega_1}$$. In the problem statement, you were given that $\omega_0 = 1\mathrm{kHz}$, $\beta \sim 2\pi \times 100\mathrm{mHz}$, and $\Delta \sim 2\pi \times 1\mathrm{mHz}$. From this, you can conclude that $\sqrt{\beta^4 + \Delta^2 \omega_0 ^2} \approx \omega_0 \Delta$ with a truncation error on the $10^{-4}$ level. Therefore, the normal mode frequencies are, to very good approximation, $$\omega_{\pm} = \omega_1 - \frac{\beta^2}{2\omega_1} \pm \frac{\omega_0}{2\omega_1} \Delta$$, where the $\Delta^2$ term has been dropped since it is 4 orders of magnitude smaller than the $\beta^2$ term.
Notice in the above analysis that there are two normal modes denoted by the subscript $\pm$. They are both shifted down from the uncoupled case by a common-mode shift of $\frac{\beta^2}{2\omega_1}$ and they are shifted apart by a splitting of $\frac{\omega_0}{\omega_1} \Delta \approx \Delta$. This suggests that you can measure $\Delta$ by measuring the beat frequency of the two normal modes. To do this, you want to prepare both modes with equal amplitudes initially. The neat thing is, you don't actually need to find the normal mode coordinates. Because the equations of motion are symmetric under interchanging $x_a$ and $x_b$, you know the normal mode eigenvectors will be identical under a parity flip. In other words, if normal mode #1 contains 90% of $x_a$ and 10% of $x_b$, then normal mode 2 will contains 90% of $x_b$ and 10% of $x_a$. (If this weren't true, then you'd have to conclude that the physical system discriminates between $x_a$ and $x_b$, which it doesn't to leading order.) Thus, you know that any initial state where $\dot{x}_a = \dot{x}_b = 0$ and $x_a = x_b$ will contain equal weights in both normal modes. Thus, you can prepare that state and watch the beat signal in the quantity $x_b - x_a$, as in the hints I shared. As I hinted, you can find this out with much less headache by playing with a numerical simulation.
Now that you have a way to measure $\Delta$, you can get a frequency uncertainty by measuring the slope of the envelope of $(x_b - x_a)e^{+\gamma t}$ (see Figure below, where the red trace is $x_a + x_b$ and the blue trace is $(x_b-x_a)e^{+\gamma t}$). The beat signal (with the exponential decay multiplied out like above) goes like $x_0 \sin(\Delta t) \cos(\omega_0 t) \approx x_0 \Delta t \times \cos(\omega_0 t)$, which you can verify with the numerical code.

Thus, you can extract $\Delta$ by measuring out to near decay time ($T = \frac{1}{\gamma}$) at a point where $\omega_0 t = 2n\pi$ and taking the slope of the envelope divided by the initial amplitude. This gives an uncertainty on $\Delta$ of $\sigma_\Delta \approx \gamma \frac{\sigma x}{x(0)} = 2.6\times 10^{-7} \times 125 \mathrm{s}^{-1} = 2\pi \times 5\mathrm{\mu Hz}$. This takes two measurements: one position measurement on each spring.

A quick bit of commentary on problem 1: Many of today's top precision measurements are frequency measurements, and often involve comparing different frequency measurements to suss out systematics (like the coupling $\beta$). This challenge was intended to train folks to thresh interesting effects ($\Delta$) from non-interesting ones ($\beta$), without having to learn the nuts and bolts of modern precision measurements. It ended up being more work than it was worth, I think. Needed to be shorter and sweeter.

Edit: fixed a rogue factor of 2

 

[Twigg]

Alright, last one:

Spoiler: Problem 3

This one is mostly a data analysis problem. For starters, note that $V_S$, $V_A$, and $V_B$ are all noisy signals. A quick bit of Kirchkoff laws analysis will show that $$V_A = \frac{V_S}{2}$$ (it's a voltage divider). Likewise, since the other side of the bridge is also a voltage divider,$$V_B = \frac{R}{2R+\delta R} V_S = \frac{V_S }{2} \left( 1 + \frac{\delta R}{2R} \right)^{-1} \approx \frac{V_S}{2} \left( 1 - \frac{\delta R}{2R}\right)$$
Taking $V_A - V_B$, $$V_A - V_B \approx V_S \left(\frac{\delta R}{4R}\right)$$
Finally, if we divide by $V_S$, then we get $$\frac{V_A - V_B}{V_S} \approx \frac{\delta R}{4R}$$ Since this quantity doesn't depend on the voltages, only on $\delta R$, it only contains the pink noise (no white noise mixed in).

With that much worked out, the next step is to load the data into your preferred data analysis software and get an estimate of the power spectral density (PSD for short). I used python, because it's the free-est.
Step-by-step, what I did is import the data and take the ratio I defined above of the voltage columns. I then take a PSD estimate using the Welch periodogram method. Since the PSD of pink noise goes as $PSD = \frac{A}{\omega}$, I find the constant A by doing linear regression on the logarithm of the data: $$\ln (PSD) = \ln A - \ln \omega$$ The estimated intercept from the linear regression gives the constant A.

Here's my analysis code:

import numpy as np
from scipy import signal
import matplotlib.pyplot as plt
import statsmodels.api as sm
import pandas as pd

# Import data
df = pd.read_csv('pinkdatafinal.csv')
#display(df)
time = df['Time(s)']
pinknoise = df['Signal(V)']

# Define sampling frequency
fs = 1/np.diff(time)[1]
#print(fs)

#Take Welch periodogram of signal
fpsd,pinkpsd = signal.welch(pinknoise,fs,scaling='density',nperseg=256)

#Plot the Welch PSD
plt.figure(2)
plt.loglog(fpsd,pinkpsd,'*')
plt.xlabel('Frequency (Hz)')
plt.ylabel('Spectral Density (V**2/Hz)')
plt.title('Pink Noise ')

#Do a linear fit of the Welch PSD on a log-log scale
flog = [np.log(f) for f in fpsd[1:]]
plog = [np.log(p) for p in pinkpsd[1:]]
x = sm.add_constant(flog)
model = sm.OLS(plog,x)
results=model.fit()
print(results.summary())#Plot the linear fit
plt.figure(2)
coef = results.params
plt.loglog(fpsd,[np.exp(coef[0] + coef[1]*np.log(f)) for f in fpsd],'--')
plt.legend(['Raw data','Fitted model'])

covss = results.cov_params()
A = 2*np.pi*np.exp(coef[0])
stdA = A*np.sqrt(covss[0][0])
print(str(A)+'('+str(stdA)+')')

And here's my output results:

The results reported there don't include a factor of 2pi, so with that taken into account, my final answer was $$A = 3.49(28) \times 10^{-7} \mathrm{\Omega}^2$$