Explaining Relative Simultaneity

[matheinste]

Yea, I was not saying anyting about the order in which events occured. I was talking about the order in which they were seen.

I cannot put it any more simply that both relative motion and position are key factors in determining when an event is seen.

You already agreed relative motion is a factor.

Now, assume an event is located at postive x-axis 4.

Now assume a and b are in the same frame relative to the event toward the negative xaxis and both are in the same frame but a is one unit more negative than b.

Clearly, whenever the event strikes at 4, b will see it first and a second because of position and not relative motion because they are in the same frame and not in the same frame as the event.

Thus, one cannot discount initial distance to the event as a factor.

So, I simply stated both as possible conditions, are you saying this is not true?

If you are talking about when an event or events are seen then I agree that it is position dependent. And also that the order in which they are seen is also thus dependent. So if you are talking about what is seen then I agree.

However, it is your statement below that I disagree with.

----the ordinality of the two light sources in terms of which occurred in which order. That is determined by the position and relative velocity.----

You use the word occurred and this is not normally taken to mean seen. For observers at rest relative to each other, when events occur is not position dependent. When thay are seen is position dependent.

Matheinste.

 

[Grimble]

This would be different than Einstein's scenario--if AB and A'B' had the same proper length, and the train was in motion relative to the embankment, then in both the embankment frame and the train frame AB and A'B' would be different lengths, so if the two strikes happened simultaneously at AB in the embankment frame, the strikes could not coincide with both A' and B' as well.

Yes, indeed, Jesse, this is a different circumstance

In this case I am saying that we stipulate that AB equals A'B';
that the lightning strikes at A and B are simultaneous (in the frame of the embankment);
and that when the lightning strikes, A and A' are adjacent.

Now if the spacetime interval between two events is the same in any frame of reference,

The "separation" between two events (points in spacetime) is a spacetime vector, the four dimensional analogue of a displacement vector in three dimensional space. The length of this vector (called the spacetime "interval") is the same in all frames:

|| \mathbf{s} || = \sqrt[]{\left| (c \; \Delta t)^{2} - (\Delta x)^{2} \right|},

where \Delta x is the distance in space between the events, and (\Delta t)^{2} the time between them. For this equation to hold, and for the length of this vector to be the same in all frames, if a given pair of events are further apart in time in one frame than another, they must also be further apart in space. As you can see, the spacetime interval between the two events is equal to the spatial distance between them in the embankment's rest frame where there's no difference in time between them (and only in that frame).

And we know that A and A', being adjacent are two references for the same event and that
A'B' is equal to AB, then by the above definition they not only have the same spacetime interval, it comprises the same terms. I.E. if the lengths are equal, then the times must be equal too

So we have AB simultaneous in the embankment's frame and A'B' simultaneous in the train's frame, yet as seen in either frame this cannot occur as the other's distances will be length contracted.

As you say:

The space time interval between what pair of events? The lightning strikes? Again, if you make AB and A'B' the same proper length, and still have the strikes be simultaneous in the embankment frame, then the strikes won't be next to both A' and B' on the train. So, the delta-x' for the two strikes in the train frame would not be equal to the distance A'B' in this case.

So what is wrong here?

P.S. as another little musing, if we are talking about relativity, then surely relativity is reciprocal - we can switch the participants and the relationship remains the same?

Something doesn't fit here : :

 

[cfrogue]

If you are talking about when an event or events are seen then I agree that it is position dependent. And also that the order in which they are seen is also thus dependent. So if you are talking about what is seen then I agree.

However, it is your statement below that I disagree with.

----the ordinality of the two light sources in terms of which occurred in which order. That is determined by the position and relative velocity.----

You use the word occurred and this is not normally taken to mean seen. For observers at rest relative to each other, when events occur is not position dependent. When thay are seen is position dependent.

Matheinste.

Oh, yes, then we are in agreement. It was poor wording on my part. Here is another statement to the effect.

both relative motion and position are key factors in determining when an event is seen.

Occurred to me in this case means when it was seen.

I was talking about the observers and the ordinality in which the strikes occurred to them.

I clearly indicated, this ordinality can differ among the observers based on relative velocity and initial position though that is most likely not known, it is a factor.

The poster was suggesting an invariant space time interval implied an invariant ordinality for the strikes. I was showing that implication is not valid as each observer in collinear relative motion will see the strikes occur at different times and further at possibly a different ordinality, meaning the order of the strikes.

 

[matheinste]

Hello cfroque,

Just for clarification, I think that in normal usage the time in an inertial frame at which an event is seen is the time coordinate of the observer, whereas the time at which it occurred is the the time coordinate of the event.

Matheinste.

 

[Grimble]

The poster was suggesting an invariant space time interval implied an invariant ordinality for the strikes. I was showing that implication is not valid as each observer in collinear relative motion will see the strikes occur at different times and further at possibly a different ordinality, meaning the order of the strikes.

Hello cfrogue, thanks for your help with this question but I am a little perplexed by your reference to an invariqant ordinality for the strikes.

As far as I am concerned I made no reference to how this situation was seen.
My point is concerned with spacetime intervals.

We have A adjacent to A', an event.
We have two lightning strikes at A and B with A occurring when A and A' are adjacent.
A and B are simultaneous in the embankment frame, that is a stipulation (a 'given').
The spacetime interval that separates events A and B has two terms: LaTeX Code: {(c \\Delta t)^2} and LaTeX Code: {\\Delta x^2} .
Now, as A and B are simultaneous the time element is equal to their spatial separation;
and as A'B' is the same distance in the trains frame as AB in the embankment's frame (when both are in proper units); these two terms are equal across the frames.
Therefore as the spacetime interval has to be the same in both frames and the distances are identical then the times also have to be identical. Therefore the lightning strikes also occur simultaneously in the train's frame.

This argument has nothing to do with ordinality, or where anything is seen from; it is all to do with a common event, a common distance between points in each of two frames and the fact that a spacetime interval is the same in all frames.

The outcome as far as I can work it out, is that Mand M' will each see the lightning strikes as simultaneous - in their own frames but that neither will see the other as simultaneous.

 

[cfrogue]

Hello cfroque,

Just for clarification, I think that in normal usage the time in an inertial frame at which an event is seen is the time coordinate of the observer, whereas the time at which it occurred is the the time coordinate of the event.

Matheinste.

OK, but with the train/embankment experiment,
Einstein said:
Observers who take the railway train as their reference-body must therefore come to the conclusion that the lightning flash B took place earlier than the lightning flash A. We thus arrive at the important result:

http://www.bartleby.com/173/9.html

Since this is a R of S thread, took place earlier and occured earliermean the same thing. The observation is that of the observer which is what I said.

But, it is just semantics.

You and I agree conceptually.

 

[matheinste]

My point is concerned with spacetime intervals.

We have A adjacent to A', an event.
We have two lightning strikes at A and B with A occurring when A and A' are adjacent.
A and B are simultaneous in the embankment frame, that is a stipulation (a 'given').
The spacetime interval that separates events A and B has two terms: {(c \Delta t)^2} and {\Delta x^2} and that these two terms are equal.

Now, as A and B are simultaneous the time element is equal to their spatial separation.
But A'B' is the same distance in the trains frame as AB in the embankment's frame when both are in proper units.
Therefore as the spacetime interval has to be the same in both frames and the distances are identical then the times also have to be identical. Therefore the lightning strikes also occur simultaneously in the train's frame.

If two events are simultaneous in an inertial frame their time separation is zero in that frame.

The spatial and time components are equal only if a photon can be present at both events, whch is impossible non colocated simultaneous events.

Matheinste

Matheinste.

 

[cfrogue]

Hello cfrogue, thanks for your help with this question but I am a little perplexed by your reference to an invariqant ordinality for the strikes.

As far as I am concerned I made no reference to how this situation was seen.
My point is concerned with spacetime intervals.

We have A adjacent to A', an event.
We have two lightning strikes at A and B with A occurring when A and A' are adjacent.
A and B are simultaneous in the embankment frame, that is a stipulation (a 'given').
The spacetime interval that separates events A and B has two terms: {(c \Delta t)^2} and {\Delta x^2} and that these two terms are equal.

Now, as A and B are simultaneous the time element is equal to their spatial separation.
But A'B' is the same distance in the trains frame as AB in the embankment's frame when both are in proper units.
Therefore as the spacetime interval has to be the same in both frames and the distances are identical then the times also have to be identical. Therefore the lightning strikes also occur simultaneously in the train's frame.

This argument has nothing to do with ordinality, or where anything is seen from; it is all to do with a common event, a common distance between points in each of two frames and the fact that a spacetime interval is the same in all frames.

The outcome as far as I can work it out, is that Mand M' will each see the lightning strikes as simultaneous - in their own frames but that neither will see the other as simultaneous.

Yes, but you forgot to mention you said also the below in the same post.

So I suppose that what I am asking is: if A and A' are adjacent and if the distance AB in the embankment's frame is equal to the distance A'B' in the train's frame then would this not be a definition of simultaneity between two events in two frames rather than simultaneity between two events in one frame?

So, from my POV you are arguing that invariant space time intervals implies invariance with respect to two events as well since you said a definition of simultaneity between two events in two frames .

Perhaps, I am misreading what you are saying.

 

[Grimble]

If two events are simultaneous in an inertial frame their time separation is zero in that frame.

The spatial and time components are equal only if a photon can be present at both events, whch is impossible non colocated simultaneous events.

Matheinste

Matheinste.

Many apologies, you are quite right, it was badly worded - editing error! I should preview more carefully before posting

Let me rephrase:
The spacetime interval that separates events A and B has two terms: {(c \Delta t)^2} and {\Delta x^2}.
Now, as A and B are simultaneous the time element is equal to their spatial separation;
and as A'B' is the same distance in the trains frame as AB in the embankment's frame (when both are in proper units); these two terms are equal across the frames.

Hopefully that clarifies what I am asking?

Grimble

 

[Grimble]

Yes, but you forgot to mention you said also the below in the same post.




So, from my POV you are arguing that invariant space time intervals implies invariance with respect to two events as well since you said a definition of simultaneity between two events in two frames .

Perhaps, I am misreading what you are saying.

Sorry again

It was all a question, not a statement.

I am unsure how to refer to it as it doesn't seem to fit any labels.

We have:

1) Due to the spacetime interval being the same in all frames;
2) comprising only two terms;
3) one of them being the same in two separate frames,
4) but ONLY in those two frames:

we arrive at the other term, the temporal separation (zero = simultanaity?) being the same but again ONLY in those two frames.

Now is the time being common across two frames, but only two frames, simultaneity or invariance?

Grimble

 

[cfrogue]

Sorry again

It was all a question, not a statement.

I am unsure how to refer to it as it doesn't seem to fit any labels.

We have:

1) Due to the spacetime interval being the same in all frames;
2) comprising only two terms;
3) one of them being the same in two separate frames,
4) but ONLY in those two frames:

we arrive at the other term, the temporal separation (zero = simultanaity?) being the same but again ONLY in those two frames.

Now is the time being common across two frames, but only two frames, simultaneity or invariance?

Grimble

I'm sorry Grimble. I cannot figure out what you are asking.

Perhaps, someone else can answer this.

 

[JesseM]

Yes, indeed, Jesse, this is a different circumstance

In this case I am saying that we stipulate that AB equals A'B';
that the lightning strikes at A and B are simultaneous (in the frame of the embankment);
and that when the lightning strikes, A and A' are adjacent.

So then do you understand that when the lightning strikes at B, B and B' are not adjacent? (Remember that all frames must agree on whether two events occur at the same position and time, so all frames will agree that the second strike did not occur at B')

Now if the spacetime interval between two events is the same in any frame of reference,

And we know that A and A', being adjacent are two references for the same event and that
A'B' is equal to AB, then by the above definition they not only have the same spacetime interval, it comprises the same terms. I.E. if the lengths are equal, then the times must be equal too

Why do you say that? If the second lightning strike does not occur at B', then the distance between the two strikes in the train frame is not equal to the distance A'B'. For this reason, the fact that A'B' is equal to AB does not imply that the distance between the two strikes is equal in both frames, in fact the distance would be different in each frame. Do you disagree?

Just to pick an example, suppose the train is moving relative to the embankment at 0.6c, and that the distance between the two strikes in the embankment frame is 10 light-seconds, and that this is the rest length of the train as well. Suppose the left strike occurs at x=0 light-seconds, t=0 seconds in the embankment frame, and the right strike occurs at x=10 l.s., t=0 s. If the left end of the train is at x=0 at t=0, then since the train's length is contracted to \sqrt{1 - 0.6^2}*10 = 0.8*10 = 8 light seconds, the right end of the train must be at x=8 l.s. at t=0 s in the embankment frame...so in this frame we predict that the right end of the train is not struck by lightning, and since all frames must agree in their predictions about which events locally coincide, this must be true in the train frame as well. To figure out what position the right strike occurs in the train frame, we can take the coordinates in the embankment frame and plug them into the Lorentz transformation:

x' = gamma*(x - vt)
t' = gamma*(t - vx/c^2)
with gamma = 1/sqrt(1 - v^2/c^2)

In this case we have gamma=1.25, and since the right strike occurred at x=10 l.s., t=0 s in the embankment frame, we can plug this into find the x' and t' coordinates of the same event in the train frame:

x' = 1.25*(10 - 0.6*0) = 12.5 light seconds
t' = 1.25*(0 - 0.6*10/1) = -7.5 seconds

So, these are the coordinates of the right strike in the train frame. The Lorentz transformation is also based on the assumption that the origins of the two frames coincide (x=0, t=0 coincides with x'=0, t'=0), so since the left strike occurred at x=0, t=0 in the embankment frame, the left strike must have occurred at x'=0, t'=0 in the train frame. Thus in the train frame the distance between the two strikes was 12.5 light seconds, and the time between them was 7.5 seconds. Plug this into the formula for the invariant interval and you get \sqrt{12.5^2 - (-7.5)^2} = \sqrt{156.25 - 56.25} = \sqrt{100} = 10, which is the same as what you get when you plug the distance and time in the embankment frame (10 light-seconds and 0 seconds) into the same formula.

So we have AB simultaneous in the embankment's frame and A'B' simultaneous in the train's frame, yet as seen in either frame this cannot occur as the other's distances will be length contracted.

What cannot occur? If the strike at B does not coincide with B', then the two strikes do not occur at A' and B', so the distance A'B' does not appear in the calculation of the spacetime interval between the two strikes. Are you suggesting we add a third lightning strike at B' that is simultaneous with the strike at A and A'? If so, this would be fine, I don't see what you think "cannot occur". Using the above coordinate systems, if we have a third strike at x'=10, t'=0 in the train frame (which is the position of the end of the train, and which is simultaneous with the first strike at x'=0, t'=0 in this frame), then we can just use the inverse Lorentz transformation to find the coordinates of this event in the embankment frame:

x = gamma*(x' + vt')
t' = gamma*(t' + vx'/c^2)

So, the third strike's coordinates in the embankment frame would be:

x = 1.25 * (10 + 0.6*0) = 12.5 light seconds
t = 1.25 * (0 + 0.6*10/1) = 7.5 seconds

So, in the embankment frame this third strike is not simultaneous with the first strike, which occurred at x=0 and t=0 in the embankment frame. But the spacetime interval between the third strike and the first strike is 10, just like the spacetime interval between the second strike and the first strike.

 

[Grimble]

So then do you understand that when the lightning strikes at B, B and B' are not adjacent? (Remember that all frames must agree on whether two events occur at the same position and time, so all frames will agree that the second strike did not occur at B')

Yes, I do understand what you are saying but please consider the following diagrams:

http://img697.imageshack.us/img697/8710/train15.jpg

Taking the situation described by Einstein where he states quite clearly

But the events A and B also correspond to positions A and B on the train.

Figures 1 and 2 show this and the corresponding spacetime coordinates. They have to be the same, therefore the event A/A' and B/B' must take place at the same time, they have identical spacetime coordinates and as it is is given that A and B are simultaneous, how can A' and B' not be simultaneous in their own reference frames?

Einstein is quite right as shown in figure 4 that the lightning strikes will not be simultaneous to the train, as observed with reference to the embankment.

However, as seen in figures 3 and 5 they will be seen from the train just as they are seen from the embankment, after all that is relativity.

So what concerns me is that there is something here that doesn't add up and I can't see what it is.

Grimble.

 

[Janus]

I don't know if this will help much, but here are two animations showing events from both the frames of the embankment and the train.

From the the embankment:

from the train:

Note that the position of the train observer relative to the embankment is the same when he sees each flash in both frames and that in both frames the embankment observer sees the flashes at the same time.

 

[matheinste]

Hello Grimble,

I am in a hurry so the reasoning below is a bit rambling and not very ordered but I think everything relevant is in there

The lightning strikes in your diagrams 2 and 5, shown in the train rest frame are 4 light seconds apart. In diagram 4, the embankment rest frame you have also shown them 4 light seconds apart. The spatial separation cannot be the same in both frames. The spacetime coordinates are not the same in both frames. Remember the definition of length is taken as a measurement between two points at the same time, or simultaneouly. So if the distance between strikes AB (or A'B') is 4 light seconds when shown in the embankment frame where the strikes are simultaneous it is not 4 light seconds in the train frame.

The train's length appears contracted as viewed form the embankment frame and vice versa; that is symmetrical. BUT the scenario is not symmetrical in all respects because the lightning strikes are defined to be simultaneous in the frame of the embankment.

In this scenario the rest length, or proper length, of the train would be greater than that of the rest length, or proper length, of the distance between the strikes.

The scenario is set up to show that the strikes cannot be simultaneous in both frames by setting the strikes to be simultaneous in the embankment frame and showing that they cannot also be simultaneous in the train frame. Of course you could, if you wished, do the opposite and set the strikes to be simultaneous in the train frame and so show that they cannot also be simultaneous in the embankemnt frame. However in this second case the rest length of the distance between strikes in the embankment frame would be longer than the rest length of the train.

Of course these lengths are not normally taken into consideration because the thought experiment is only designed to show the frame dependence of simultaneity.

I hope this is of some help

Matheinste.

 

[JesseM]

Yes, I do understand what you are saying but please consider the following diagrams:

http://img697.imageshack.us/img697/8710/train15.jpg

You say you understand what I am saying, but the diagrams show you clearly don't! These diagrams are incompatible according to relativity--in diagram 1 you show the distance between A and B as 4 in the embankment frame, in diagram 2 you show the distance between A' and B' as also being 4 in the train frame, but then in diagram #4, drawn from the perspective of the embankment frame, you show A' and B' lining up with A and B at t=0! This is just wrong, if the distance between A' and B' is 4 in their own rest frame, then in the embankment frame the distance between A' and B' should be shorter than 4 due to length contraction, so if A lines up with A' at t=0 in the embankment frame, then B' should be somewhere short of 4 at t=0 (for example, if v=0.6c, then at t'=0, B' would be at position 3.2). You have to either change the rest length of the train (changing diagram 2 so that the train's rest length is greater than 4, so its contracted length in the embankment frame can be 4), or else redraw diagram #4 to show that the worldline of B' starts at some position short of 4 on the x-axis of the embankment frame.

 

[Janus]

Yes, I do understand what you are saying but please consider the following diagrams:

http://img697.imageshack.us/img697/8710/train15.jpg

Taking the situation described by Einstein where he states quite clearly

Figures 1 and 2 show this and the corresponding spacetime coordinates. They have to be the same, therefore the event A/A' and B/B' must take place at the same time, they have identical spacetime coordinates and as it is is given that A and B are simultaneous, how can A' and B' not be simultaneous in their own reference frames?

Einstein is quite right as shown in figure 4 that the lightning strikes will not be simultaneous to the train, as observed with reference to the embankment.

However, as seen in figures 3 and 5 they will be seen from the train just as they are seen from the embankment, after all that is relativity.

So what concerns me is that there is something here that doesn't add up and I can't see what it is.

Grimble.

Here's the actual S-T diagrams from each frame:

http://home.earthlink.net/~parvey/sitebuildercontent/sitebuilderpictures/simul.gif

The point is that both frames have to agree that M' does not see both flashes at the same time. Anything else would result in physical contradictions. And since only way that this can be true in the Train's frame, (Since M is an equal distance from A' and B') is for the strikes not to have taken place simultaneously in that frame.

 

[Grimble]

Thank you, good people for your comments, (and I do accept that in diagram 4 I neglected the length contraction - sorry)

I have therefore redrawn it:

http://img4.imageshack.us/img4/4831/train2r.jpg

But, back to the point I was raising, if we consider the spacetime coordinates at the time of the lightning strikes in the embankment frame we have:
A = 0,0,0,0
M = 0,2,0,0
B = 0,4,0,0

While at the same time, when A and A' are adjacent in the Train's frame we have:
A' = 0,0,0,0
M' = 0,2,0,0
B' = 0,4,0,0

Now the two frames with which we are concerned are inertial frames, their units are proper units.
They have a common origin the event of kightning striking A, when A' is adjacent to A.

This has NOTHING to do with what is seen of one frame by any observer in the other frame.

This is solely about the spactime coordinates of six points in two separate frames of refrence that have a common origin.

If they are both inertial frames, if therefore they have common units, and if two points have the same coordinates, then they must represent the same event.

Therefore the lightning must hit B' at the same time as B and the lightning strikes must be simultaneous in both frames of reference, but only in those frames of reference, not in one frame viewed from the other.

So where am I going wrong?

Grimble

 

[matheinste]

Hello Grimble.

But, back to the point I was raising, if we consider the spacetime coordinates at the time of the lightning strikes in the embankment frame we have:
A = 0,0,0,0
M = 0,2,0,0
B = 0,4,0,0

While at the same time, when A and A' are adjacent in the Train's frame we have:
A' = 0,0,0,0
M' = 0,2,0,0
B' = 0,4,0,0

This is incorrect. The coordinates are not the same in both frames.

This is obvious for the time coordinate of B' as it icannot have the same time coordinate of A' as the strikes are not simultaneous in the train frame, as has already been established.

Matheinste.

 

[Janus]

But, back to the point I was raising, if we consider the spacetime coordinates at the time of the lightning strikes in the embankment frame we have:
A = 0,0,0,0
M = 0,2,0,0
B = 0,4,0,0

While at the same time, when A and A' are adjacent in the Train's frame we have:
A' = 0,0,0,0
M' = 0,2,0,0
B' = 0,4,0,0

No, for example if the relative speed of the train to the embankment is 0.5c:

Then in the embankment frame, the distance between A and B is 4 light sec, and the distance between A' and B' is 4 light sec. This is the proper distance between A and B and the length contracted distance between A'and B'

Therefore, in the train frame, the proper distance between A' and B' is 4.62 light sec, and the length contracted distance between A and B is 3.46 light sec.

Therefore, in the embankment frame, when A is next to A'
we get

A = 0,0,0,0
M = 0,2,0,0
B = 0,4,0,0

And
A' = 0,0,0,0
M' = 0,2,0,0
B' = 0,4,0,0

but in the train frame we would get:

A = 0,0,0,0
M = 0,1.73,0,0
B = 0,3.46,0,0

And
A' = 0,0,0,0
M' = 0,2.32,0,0
B' = 0,4.62,0,0

Assuming that both frames assign the zero time coordinate to the moment that A' and A meet, then while both point B and B' are the same distance from AA' in the embankment frame at t=0, B' is further from AA' than B is in the train frame at t=0. B' has already past B and therefore B and B' met before t=0

 

[JesseM]

Thank you, good people for your comments, (and I do accept that in diagram 4 I neglected the length contraction - sorry)

I have therefore redrawn it:

http://img4.imageshack.us/img4/4831/train2r.jpg

The altered diagram still shows the worldline of B' intersecting with B at x=4 in the embankment frame. Are the new red lines supposed to be the light rays as seen in the train frame? You can't combine what's seen in the embankment frame and what's seen in the train frame in a single diagram, a spacetime diagram in SR is supposed to represent the perspective of one frame. There should only be a single pair of lines representing the light rays, to fix diagram #4 you need to erase the current B' worldline and draw a new one (still parallel to the A' worldline) that intersects the x-axis at a different position than x=4, showing that at t=0 in the embankment frame, the distance between A' and B' is less than 4 due to length contraction.

But, back to the point I was raising, if we consider the spacetime coordinates at the time of the lightning strikes in the embankment frame we have:
A = 0,0,0,0
M = 0,2,0,0
B = 0,4,0,0

While at the same time, when A and A' are adjacent in the Train's frame we have:
A' = 0,0,0,0
M' = 0,2,0,0
B' = 0,4,0,0

Now the two frames with which we are concerned are inertial frames, their units are proper units.
They have a common origin the event of kightning striking A, when A' is adjacent to A.

This has NOTHING to do with what is seen of one frame by any observer in the other frame.

This is solely about the spactime coordinates of six points in two separate frames of refrence that have a common origin.

If they are both inertial frames, if therefore they have common units, and if two points have the same coordinates, then they must represent the same event.

Therefore the lightning must hit B' at the same time as B and the lightning strikes must be simultaneous in both frames of reference, but only in those frames of reference, not in one frame viewed from the other.

You're not making any sense to me. What do you mean "if therefore they have common units"? By definition different frames have different ways of assigning coordinates to the same event. If the second lightning strike occurs at x=4 and t=0 in the embankment frame, its coordinates of the second strike are different in the train frame. Do you understand what the "Lorentz transformation" is? Its whole purpose is to take the coordinates assigned to a single physical event in one frame, and tell you the different set of coordinates assigned to that same physical event in another frame. If an event has coordinates x,t in one inertial frame, and we want to know the coordinates x',t' assigned to that same event in a different inertial frame whose spacetime origin coincides with the first frame (i.e. an event at x=0 and t=0 in the first frame has coordinates x'=0 and t'=0 in the second frame) and which is moving at speed v relative to the first frame, then the Lorentz transformation gives the answer:

x' = gamma*(x - vt)
t' = gamma*(t - vx/c^2)
with gamma = 1/sqrt(1 - v^2/c^2)

Try picking a value for v (v=0.6c is a nice one, it leads to a gamma factor of 1.25) and then plugging in the event (x=4, t=0), you'll see that the x' and t' coordinates of this event are different.

 

[Grimble]

Hello Grimble.

This is incorrect. The coordinates are not the same in both frames.

This is obvious for the time coordinate of B' as it cannot have the same time coordinate of A' as the strikes are not simultaneous in the train frame, as has already been established.

Matheinste.

Then tell me what the coordinates are.

Assuming that both frames assign the zero time coordinate to the moment that A' and A meet, then while both point B and B' are the same distance from AA' in the embankment frame at t=0, B' is further from AA' than B is in the train frame at t=0. B' has already past B and therefore B and B' met before t=0

There is no reference to LT, because all I am doing is looking at the spacetime coordinates of the two separate frames.
LT is only relevant when observing one from the other.
In each frame all the units are proper units.
You are describing how the train will look from the embankment, which involves their relative velocity and the length contraction that is dependent thereon. If that velocity changed so would your values for the train's coordinates, which has nothing to do with the train's spacetime coordinates, in the train's frame of reference, considered purely on it's own.
I am only comparing the spacetime coordinates after calculating what they are; considering that we have one common event and then seeing how they compare.

The altered diagram still shows the worldline of B' intersecting with B at x=4 in the embankment frame. Are the new red lines supposed to be the light rays as seen in the train frame? You can't combine what's seen in the embankment frame and what's seen in the train frame in a single diagram, a spacetime diagram in SR is supposed to represent the perspective of one frame. There should only be a single pair of lines representing the light rays, to fix diagram #4 you need to erase the current B' worldline and draw a new one (still parallel to the A' worldline) that intersects the x-axis at a different position than x=4, showing that at t=0 in the embankment frame, the distance between A' and B' is less than 4 due to length contraction.

Yes, very good! but the red lines were to shew that that diagram was wrong and the replacement is just below it and agrees with your comments -- I think!

You're not making any sense to me. What do you mean "if therefore they have common units"? By definition different frames have different ways of assigning coordinates to the same event.

OK let me restate this so you can understand what I am saying.

We have two inertial frames of reference.
They have identical physical laws.
Therefore identical clocks and measuring devices must keep identical time and measurements in each frame.
We do therefore have common units

In the first frame, the embankment, we describe the space time coordinates of three events; A,M,B.

AM = 2 light-seconds and MB = 2 lightseconds. All three have a time = 0

In the second frame, the train, we describe another three points, A',M',B'.

A'M' = 2 light-seconds and M'B' = 2 lightseconds. All three have a time = 0

Then if event A and event A', coincide, i.e. are adjacent, then M and M', and B and B' must also coincide.

Now as lightning strikes A and B simultaneously at the events A/A' and B/B' they must be simultaneous in each frame.

None of this has anything to do with Lorentz Transformations.
We are considering the spacetime coordinates of each frame, from that same frame, from which point of view that frame is at rest.

When we expand this to view how this appears relative to an observer in each reference frame then LT is of prime imortance and length contraction would be evident.

If you consider that this reasoning is mistaken please tell me what the spacetime coordinates would be. For the spacetime coordinates of one frame must be made from the point of view that an observer within that same frame considers it to be stationary.

Grimble

 

[matheinste]

----------Now as lightning strikes A and B simultaneously at the events A/A' and B/B' they must be simultaneous in each frame.----------

This is wrong.

The basic Einstein thought experiment already explains this fact. The strikes are simultaneous in the embankment frame. That is given. They are not simultaneous in the train frame. That is derived by logic from the postulates. So if you choose to assign the same coordinate to A snd A' when viewed from both frames ( effectively making those events occur at the origin in both frames ), then if B and B' have the same time coordinate as each other in the embankment frame, which is how the scenario is set up, they cannot have the same time coordinate as each other in the train frame. The same applies to M and M'.

Matheinste.

 

[Grimble]

----------Now as lightning strikes A and B simultaneously at the events A/A' and B/B' they must be simultaneous in each frame.----------

This is wrong.

The basic Einstein thought experiment already explains this fact. The strikes are simultaneous in the embankment frame. That is given. They are not simultaneous in the train frame. That is derived by logic from the postulates. So if you choose to assign the same coordinate to A snd A' when viewed from both frames ( effectively making those events occur at the origin in both frames ), then if B and B' have the same time coordinate as each other in the embankment frame, which is how the scenario is set up, they cannot have the same time coordinate as each other in the train frame. The same applies to M and M'.

Matheinste.

Not as seen/observed/referenced from the embankment as Einstein said but as Einstein said:

Also the definition of simultaneity can be given relative to the train in exactly the same way as with respect to the embankment.

but this has, it seems to me been mistakenly taken as referring to the definition for simultaneity. But it could just as easily/correctly be taken as meaning "the definition of simultaneity can be applied relative to the train in exactly the same way as with respect to the embankment.

Then the argument referring to the coordinates works. Otherwise we have a conflict based on nothing more than the statement that simultaneity can only happen in one frame, and as I keep saying Einstein only applied that with reference to the embankment

Grimble

 

[JesseM]

Hello Grimble.

This is incorrect. The coordinates are not the same in both frames.

This is obvious for the time coordinate of B' as it cannot have the same time coordinate of A' as the strikes are not simultaneous in the train frame, as has already been established.

Matheinste.

Then tell me what the coordinates are.

If the velocity of the train relative to the embankment is 0.6c, and in the embankment frame the first strike occurs at x=0 light-seconds, t=0 seconds while the second strike occurs at x=4 l.s., t=0 s, then in the train frame the first strike occurs at x'=0 l.s, t'=0 s and the coordinates of the second strike can be found using the Lorentz transformation:

x' = gamma*(x - vt)
t' = gamma*(t - vx/c^2)

Here gamma=1.25, so we have x' = 1.25*(4) = 5 l.s., and t' = 1.25*(-0.6*4) = -3.25 s. So, in the train frame the coordinates of the second strike are x' = 5 l.s. and t' = -3.25 s.

There is no reference to LT, because all I am doing is looking at the spacetime coordinates of the two separate frames.
LT is only relevant when observing one from the other.

I've already told you this notion of frames "observing" each other doesn't make any sense to me, the Lorentz transformation simply tells you the coordinates of a single spacetime event in one frame's own coordinates if you know the coordinates of the same event in the other frame. As I said back in post #28:

If the events aren't simultaneous in the train frame, then by definition both frames do not "both agree it was simultaneous". When physicists use anthropomorphic language about frames, like talking of frames making judgments or agreeing about things, they do not mean to imply that frames can "think" about any other frame besides themselves and form opinions about what is true in that other frame; a "judgment" made by a frame is just a fact which you arrive at by making an analysis that involves the coordinates of that frame alone, like the judgment that two events are simultaneous in that frame (they happen at the same t-coordinate), and for two frames to "agree" on something just means that a thing which is true when you analyze it from one frame's perspective is also true when you analyze it from another frame's perspective. So it would be stretching the anthropomorphism to the point of absurdity to talk of frames making "judgments" about what is true in other frames besides themselves, or of two frames A and B "agreeing" that two events are simultaneous in A (even though they are not simultaneous in B). Trust me, physicists never talk this way.

If this point is still not clear to you, please take a look at my thread An illustration of relativity with rulers and clocks, which shows the ruler/clock systems of two different frames moving alongside each other. Although the diagrams drawn from each frame's perspective look different, you can see that they always agree on which pairs of events coincide locally, as I've discussed earlier on this thread. For example, the top part of the diagram below shows what things look like at t=1 microsecond in frame A, the bottom part shows what things look like at t'=0 microseconds in frame B, even though the two diagrams look different they both agree that the event of (A's clock at position 346.2 meters on A's ruler showing a time of 1 microsecond) coincides locally with the event of (B's clock at 173.1 meters on B's ruler showing a time of 0 microseconds).

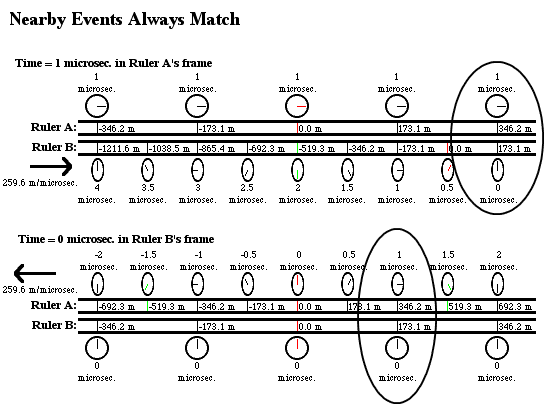
So, if there was an event like a lightning flash that occurred next to the 346.2 meter mark on A's ruler when the clock at that mark read 1 microsecond, then naturally by the principle that there are objective frame-independent truths about which events locally coincide, it would have to be true that this same lightning flash occurred next to the 173.1 meter mark on B's ruler when the clock at that mark read 0 seconds. These are just statements about what coordinates each frame assigns to the flash using their own rulers and clocks, nothing to do with one frame "observing" the other one! And this is exactly what the Lorentz transformation is designed to do--if you plug in x=346.2 meters and t=1 microsecond into the Lorentz transformation, along with v=0.866c and gamma=2 as I assumed in the diagrams, then you will in fact get x'=173.1 meters and t=0 microseconds (I showed the math in post #134 of the Time dilation formula thread).

Yes, very good! but the red lines were to shew that that diagram was wrong and the replacement is just below it and agrees with your comments -- I think!

My bad! OK, then I agree with your redrawn diagram #4.

You're not making any sense to me. What do you mean "if therefore they have common units"? By definition different frames have different ways of assigning coordinates to the same event.

OK let me restate this so you can understand what I am saying.

We have two inertial frames of reference.
They have identical physical laws.
Therefore identical clocks and measuring devices must keep identical time and measurements in each frame.
We do therefore have common units

Does "common units" mean nothing more than the idea that clocks at rest in each frame behave identically with respect to the coordinates of that frame, and likewise for rulers at rest in each frame? Of course each frame's own clocks run at a rate of 1 tick per second of coordinate time in their own frame--you can see this is true if you compare the first and second diagram in the An illustration of relativity with rulers and clocks thread, the first showing things from frame A's perspective (and showing that at t=0 microseconds in A's frame, every one of A's clocks reads 0 microseconds, then at t=1 microseconds in A's frame, every one of A's clocks reads 1 microsecond, and finally at t=2 microseconds in A's frame, every one of A's clocks reads 2 microseconds) the second showing things from frame B's perspective (and showing that at t'=0 microseconds in B's frame, every one of B's clocks reads 0 microseconds, then at t'=1 microseconds in B's frame, every one of B's clocks reads 1 microsecond, and finally at t'=2 microseconds in B's frame, every one of B's clocks reads 2 microseconds). But this notion of "common units" does not mean that an event with a given set of coordinates in A's frame (like the event in the third diagram at x=346.2 meters, t=1 microsecond in A's frame) will have the same coordinates in B's frame (in this case the event would have coordinates x'=173.1 meters, t'=0 microseconds in B's frame). So why do you think that "common units" somehow shows that if an event occurs at x=4 light seconds, t=0 seconds in one frame, it should occur at x'=4 light seconds, t'=0 seconds in the other frame? There seems to be no logical connection here.

In the first frame, the embankment, we describe the space time coordinates of three events; A,M,B.

AM = 2 light-seconds and MB = 2 lightseconds. All three have a time = 0

In the second frame, the train, we describe another three points, A',M',B'.

A'M' = 2 light-seconds and M'B' = 2 lightseconds. All three have a time = 0

Then if event A and event A', coincide, i.e. are adjacent, then M and M', and B and B' must also coincide.

Why? This is a complete non sequitur! In the embankment frame the distance A'M' is less than 2 light seconds, and in the train frame the distance AM is likewise less than 2 light seconds, so there's no reason to expect M' to coincide with M in either frame. Again, please look at the An illustration of relativity with rulers and clocks thread. Suppose I say that in frame A, event A is at (x=0 meters, t=0 microseconds) and event M is at (x=346.2 meters, t=0 microseconds). Likewise I say that in frame B, event A' is at (x'=0 meters, t'=0 microseconds) and event M' is at (x'=346.2 meters, t'=0 microseconds). By your reasoning, would you say that if events A and A' coincide, then events M and M' must coincide as well? But if you look at the diagrams, you can easily verify that events A and A' do coincide (the event of A's clock at the 0-meter mark reading 0 microseconds lines up with the event of B's clock at the 0-meter mark reading 0 microseconds) while M and M' do not coincide (the first diagram shows that the event of A's clock at the 346.2-meter mark reading 0 microseconds lines up with the event of B's clock at the 692.3-meter mark reading -2 microseconds, while the second diagram shows that the event of B's clock at the 346.2-meter mark reading 0 microseconds lines up with the event of A's clock at the 692.3-meter mark reading +2 microseconds). And yet, clearly the diagrams respect the principle that identical clocks and rulers behave identically in their own frames--in frame A, A's clocks tick forward at a rate of 1 microsecond per microsecond of coordinate time, and in frame B, B's clocks also tick forward at a rate of 1 microsecond per microsecond of coordinate time.

Please go over the diagrams and verify that what I am saying is correct, then tell me if you still think the principle that "identical clocks and rulers behave identically in their own frame" somehow implies that if A and A' coincide, M and M' coincide (if so, how do you explain the fact that the diagrams indicate otherwise, in spite of the fact that they do seem to respect the 'identical clocks and rulers behave identically in their own frame' principle?)

None of this has anything to do with Lorentz Transformations.
We are considering the spacetime coordinates of each frame, from that same frame, from which point of view that frame is at rest.

Again you appear confused about what the Lorentz transformation is for. It simply tells you which ruler/clock readings in one frame line up with which ruler/clock readings in the other--everyone should agree on which pair of readings line up, based on the principle that there must be an objective truth about which events locally coincide. And each set of ruler/clock readings represent that frame's own coordinates, nothing to do with one frame "observing" the other. Again, based on the idea that there must be an objective truth about which events locally coincide, then if a given event like a lightning flash coincides locally with the event of a clock at 346.2 meters on frame A's ruler reading a time of 1 microsecond (with both the ruler and clock at rest in frame A), and we also know that this ruler/clock reading in frame A coincides locally with the event of a clock at 173.1 meters on frame B's ruler reading a time of 0 microseconds, then obviously it must also be true that the same lightning flash coincides locally with the event of the clock at 173.1 meters on frame B's ruler reading a time of 0 microseconds, that's just the coordinates that B will assign to the same event using his own set of rulers and clocks.

If you consider that this reasoning is mistaken please tell me what the spacetime coordinates would be. For the spacetime coordinates of one frame must be made from the point of view that an observer within that same frame considers it to be stationary.

Again, the whole point of the Lorentz transform is that if you know the spacetime coordinates of an event in frame #1, it will give you the spacetime coordinates of the same event in frame #2. As I said, if the second lightning strike occurs at x=4 l.s. and t=0 s in the embankment frame, and if the train is moving at 0.6c relative to the embankment, then in the train frame's own coordinates this same lightning strike will have coordinates x'=5 l.s and t'=-3.25 s.

 

[Grimble]

First of all let me apologise to you; whenever I use the anthropomorphic language that offends you, would you please excuse me, and read it as saying that someone in that frame 'thinks'/'judges'/'agrees', I do understand how annoying something such as this can be and I will try not to do it again.

Secondly let me assure you that I do understand the points you raise but I do have some difficulty accepting them. (I must seem like hard work to you and I do appreciate the time you are spending to help me).

As far as the 'common' units are concerned, it seems to me that if one has identical clocks, kept under identical conditions the time that they keep will be identical, i.e. 1 second on one clock will be exactly equal to one second on another clock - this is after all only an extension of Einstein's own theory's statement viz:

It is clear that this definition can be used to give an exact meaning not only to two events, but to as many events as we care to choose, and independently of the positions of the scenes of the events with respect to the body of reference 1 (here the railway embankment). We are thus led also to a definition of “time” in physics. For this purpose we suppose that clocks of identical construction are placed at the points A, B and C of the railway line (co-ordinate system), and that they are set in such a manner that the positions of their pointers are simultaneously (in the above sense) the same. Under these conditions we understand by the “time” of an event the reading (position of the hands) of that one of these clocks which is in the immediate vicinity (in space) of the event. In this manner a time-value is associated with every event which is essentially capable of observation.
This stipulation contains a further physical hypothesis, the validity of which will hardly be doubted without empirical evidence to the contrary. It has been assumed that all these clocks go at the same rate if they are of identical construction. Stated more exactly: When two clocks arranged at rest in different places of a reference-body are set in such a manner that a particular position of the pointers of the one clock is simultaneous (in the above sense) with the same position of the pointers of the other clock, then identical “settings” are always simultaneous (in the sense of the above definition).

For surely any such clock, in any inertial frame of reference, will be subject to identical physical conditions, identical physical laws, and must therefore keep the same time. How could it not do so?

And I quite agree that the LT enable one to see (calculate) how the coordinates from one frame can be transformed to another frame and what they will be after transformation.

But the point I have been trying to put across is that I am looking at two separate frames and how the spacetime coordinates of each frame can be arrived at, before comparing them.

The two sets of coordinates exist entirely on their own, independent of each other.
It is only when we state that A and A' (and the lightning strike are, in fact, all one event) that we compare them. And at that time the LT have not been involved.

This is just my explanation for you.

Grimble

 

[A.T.]

But the point I have been trying to put across is that I am looking at two separate frames and how the spacetime coordinates of each frame can be arrived at, before comparing them.

What are "spacetime coordinates of each frame"? Events have spacetime coordinates, not frames. A frame defines spacetime coordinates of each event.

The two sets of coordinates exist entirely on their own, independent of each other.

The spacetime coordinates of the same unique events in each frame are not independent. They are coupled via the LT.

 

[JesseM]

First of all let me apologise to you; whenever I use the anthropomorphic language that offends you, would you please excuse me, and read it as saying that someone in that frame 'thinks'/'judges'/'agrees', I do understand how annoying something such as this can be and I will try not to do it again.

You're missing the main point, which is that the Lorentz transformation is not about what someone in one frame "judges" about another frame, it's about which ruler/clock readings in one frame objectively coincide with ruler/clock readings in another frame. Did you look over my example in the the "illustration of relativity with rulers and clocks" thread like I asked?

Secondly let me assure you that I do understand the points you raise but I do have some difficulty accepting them. (I must seem like hard work to you and I do appreciate the time you are spending to help me).

Then please actually address the questions and examples I bring up, which are intended to either convince you that you are wrong, or clarify where you disagree with me.

As far as the 'common' units are concerned, it seems to me that if one has identical clocks, kept under identical conditions the time that they keep will be identical, i.e. 1 second on one clock will be exactly equal to one second on another clock

The meaning of this statement is ambiguous. 1 second of time on clock A in clock A's rest frame is the same as 1 second of time on clock B in clock B's rest frame (they both last 1 second of coordinate time in their respective frames), but if we pick a single frame to analyze both clocks, and the clocks have different speeds in this frame, then in this frame 1 second of time on clock A is not equal to clock B. Agreed?

For surely any such clock, in any inertial frame of reference, will be subject to identical physical conditions, identical physical laws, and must therefore keep the same time. How could it not do so?

"Same time" is again ambiguous. It keeps the same time in its own rest frame as any other clock does in its own rest frame. But from the perspective of anyone frame, clocks with different speeds keep different times.

And I quite agree that the LT enable one to see (calculate) how the coordinates from one frame can be transformed to another frame and what they will be after transformation.

But the point I have been trying to put across is that I am looking at two separate frames and how the spacetime coordinates of each frame can be arrived at, before comparing them.

But what you don't seem to understand is that when we talk about "transforming into another frame", all we are talking about is finding out what x',t' coordinates that other frame assigned to the event on its own, totally independent of any use of the Lorentz transformation! That's why I am trying to steer you to discuss the specifics of my example with rulers and clocks, so that you will actually see how this works instead of just talking in generalities. Please, look at this diagram and actually think about it for just a minute!

Again, suppose an event like a lightning flash happens in the same local vicinity as the circled region. Does observer A have to use the Lorentz transformation, or to think about observer B's coordinates, in order to figure out the coordinates of the event in his frame? No, he can just take a picture of the lightning flash as it happened, and see that as the flash occurred it was right next to the 346.2 meter mark on his ruler, and that at that moment the clock attached to that mark read 1 microsecond. Likewise, does observer B have to think about observer A's coordinates or use the Lorentz transformation to figure out the coordinates of the event in his frame? No, he too can take a picture of the lightning flash as it happened, and see that as the flash occurred it was right next to the 173.1 meter mark on his ruler, and that at that moment the clock attached to that mark read 0 microsecond. The Lorentz transformation simply relates the readings that one observer will get using his own ruler/clock system to the readings another observer will get using his own ruler/clock system, it has nothing to do with introducing some new notion called "transformed coordinates" which represent one observer's view of another frame or which are fundamentally different from the coordinates each observer gets using only his own measurements.

The two sets of coordinates exist entirely on their own, independent of each other.
It is only when we state that A and A' (and the lightning strike are, in fact, all one event) that we compare them. And at that time the LT have not been involved.

Well, hopefully you agree that it's not just a matter of us arbitrarily "stating" which events coincide in spacetime, there must be an objective physical truth about this. And you're right, we do not need to ever use the Lorentz transformation if different frames actually have their own physical measurement apparatuses (like the ruler/clock systems at rest in each frame) to assign coordinates to events. It will nevertheless be true that when they compare the coordinates each has found using their own inertial measurement apparatuses, they will find after-the-fact that the coordinates will be coupled in exactly the manner predicted by the Lorentz transformation, assuming that the two postulates of relativity actually hold true. Do you disagree with this? If so, why?

 

[Grimble]

You're missing the main point, which is that the Lorentz transformation is not about what someone in one frame "judges" about another frame, it's about which ruler/clock readings in one frame objectively coincide with ruler/clock readings in another frame. Did you look over my example in the the "illustration of relativity with rulers and clocks" thread like I asked?

Yes, that makes sense, it is at last an easy way to think of it; and yes, I have been looking at your illustration, and I will do so again.

Then please actually address the questions and examples I bring up, which are intended to either convince you that you are wrong, or clarify where you disagree with me.

I will go over all you have been saying and try and do so.

The meaning of this statement is ambiguous. 1 second of time on clock A in clock A's rest frame is the same as 1 second of time on clock B in clock B's rest frame (they both last 1 second of coordinate time in their respective frames), but if we pick a single frame to analyze both clocks, and the clocks have different speeds in this frame, then in this frame 1 second of time on clock A is not equal to clock B. Agreed?

Oh yes, I agree absolutely with what you say here, but if my statement was ambiguous I need to refine my thinking and improve my expression of my thoughts.

"Same time" is again ambiguous. It keeps the same time in its own rest frame as any other clock does in its own rest frame. But from the perspective of anyone frame, clocks with different speeds keep different times.

I agree with you again but as that was not what I was saying, I must go away and think about it again!

But what you don't seem to understand is that when we talk about "transforming into another frame", all we are talking about is finding out what x',t' coordinates that other frame assigned to the event on its own, totally independent of any use of the Lorentz transformation! That's why I am trying to steer you to discuss the specifics of my example with rulers and clocks, so that you will actually see how this works instead of just talking in generalities. Please, look at this diagram and actually think about it for just a minute!

I can appreciate much of this but I do have a couple of observations:

But for another observer who sees the ship moving, the back of the ship is moving towards the point where the flash happened and the front is moving away from that point, so his own network of clocks will be synchronized in such a way that the clock next to the event "light hits the back of the ship" will read an earlier time than the clock next to the event "light hits the front of the ship".

Surely either frames clock's should be synchronised in it's own frame? That is how Einstein's clock synchronisation works, doesn't it?

In "time = 0 microse. in Ruler A's Frame" the clock marked in green at -519.3 m shews time 1.5 microsec, yet 1 micrsec. later in Ruler A's Frame, it shews 2 microsec but has advanced 519.3 m.? Which by my calculation is 1038.6 m/microsec. or almost 3.5c!??

Again, suppose an event like a lightning flash happens in the same local vicinity as the circled region. Does observer A have to use the Lorentz transformation, or to think about observer B's coordinates, in order to figure out the coordinates of the event in his frame? No, he can just take a picture of the lightning flash as it happened, and see that as the flash occurred it was right next to the 346.2 meter mark on his ruler, and that at that moment the clock attached to that mark read 1 microsecond. Likewise, does observer B have to think about observer A's coordinates or use the Lorentz transformation to figure out the coordinates of the event in his frame? No, he too can take a picture of the lightning flash as it happened, and see that as the flash occurred it was right next to the 173.1 meter mark on his ruler, and that at that moment the clock attached to that mark read 0 microsecond. The Lorentz transformation simply relates the readings that one observer will get using his own ruler/clock system to the readings another observer will get using his own ruler/clock system, it has nothing to do with introducing some new notion called "transformed coordinates" which represent one observer's view of another frame or which are fundamentally different from the coordinates each observer gets using only his own measurements.

OK.

Well, hopefully you agree that it's not just a matter of us arbitrarily "stating" which events coincide in spacetime, there must be an objective physical truth about this. And you're right, we do not need to ever use the Lorentz transformation if different frames actually have their own physical measurement apparatuses (like the ruler/clock systems at rest in each frame) to assign coordinates to events. It will nevertheless be true that when they compare the coordinates each has found using their own inertial measurement apparatuses, they will find after-the-fact that the coordinates will be coupled in exactly the manner predicted by the Lorentz transformation, assuming that the two postulates of relativity actually hold true. Do you disagree with this? If so, why?

No problem with this.

But one thing is still bothering me; if all things are relative does that mean that there are no standard units by which different frames can be related?
By this, I am thinking of inertial frames with no external forces acting upon them. In such a frame, a muon's half-life, 2.2 microseconds, would surely be the same as the half-life in another inertial frame, it is a physical property, a law, and one would think, therefore, the same in any inertial frame? And I don't mean just to say it's half-life would be the same number of microseconds, I mean that the microseconds would have the same duration in any inertial frame?

After all, this is something that can be reasoned/deduced from your https://www.physicsforums.com/showthread.php?t=59023"
In which you state:

This means that each ruler will observe the other one’s clocks tick exactly half as fast as their own, and will see the other ruler's distance-markings to be squashed by a factor of two.

And this could only be true if the two ruler's markings and clocks had identical (in magnitude) units.
So, do we imply from this, that the magnitude of the units of measurement in inertial frames will be constant? That inertial units can be taken as the 'real' units and that it is these units that are 'contracted' or 'dilated' as a function of two frames relative velocity?

In post #75 you wrote:

I've already told you this notion of frames "observing" each other doesn't make any sense to me, the Lorentz transformation simply tells you the coordinates of a single spacetime event in one frame's own coordinates if you know the coordinates of the same event in the other frame.

which is a nice concise description, however, it does lead to another consideration:
If the coordinates of 'a single spacetime event' are known in frame A, the Lorentz transformation tells (an observer in) frame B what those coordinates are in frame B.
Frame C, however, can use LT to determine the coordinates of that same event from frame B (as frame B now knows what those coordinates are in frame B's coordinates).
But if frame C were then to use LT to determine what the coordinates are from those in frame A would he get the same result? I think not??

This may seem a little contrived but consider, if Einstein had two railway tracks and two trains running through the embankment, such that A and B lined up for all three frames; and if the relative velocity between train1 and the embankment were the same as the relative velocity between train2 and the embankment, then the length AB on each train would be the same in the embankments coordinates but not from the coordinates of the other train.
(This does of course require that A is the front of one train and the back of the other)

Grimble

 

[JesseM]

Thanks for focusing on those diagrams Grimble...you ask some good questions, I'll try to address them:

I can appreciate much of this but I do have a couple of observations:

But for another observer who sees the ship moving, the back of the ship is moving towards the point where the flash happened and the front is moving away from that point, so his own network of clocks will be synchronized in such a way that the clock next to the event "light hits the back of the ship" will read an earlier time than the clock next to the event "light hits the front of the ship".

Surely either frames clock's should be synchronised in it's own frame? That is how Einstein's clock synchronisation works, doesn't it?

Yes, but that isn't contradicted by my quote above. In the ship's own frame the clocks at the front and back of the ship are synchronized, what I said was that "for another observer who sees the ship moving", the light hits the back clock on the ship later than the light hits the front clock on the ship (as measured by 'his own network of clocks', so if he looks at the time on a clock in his network which is next to the back of the ship when the light reaches it, and compares to the time on a clock in his network which is next to the front of the ship when the light reaches it, the former time will be earlier than the latter time). So he sees the two clocks on the ship being out-of-sync, since the ship observer set them both to read the same time when the light reached them.

In "time = 0 microse. in Ruler A's Frame" the clock marked in green at -519.3 m shews time 1.5 microsec, yet 1 micrsec. later in Ruler A's Frame, it shews 2 microsec but has advanced 519.3 m.? Which by my calculation is 1038.6 m/microsec. or almost 3.5c!??

But the speed of B's green clock in A's frame is defined solely by measurements of position and time on A's own rulers and clocks, not by the time on B's clock itself. If we define event #1 as "B's green clock at the -519.3 m mark on B's ruler showing a time of 1.5 microseconds", and event #2 as "B's green clock at the -519.3 m mark on B's ruler showing a time of 2 microseconds", then if you look at the diagram you can see that event #1 occurs halfway between the -173.1 meter mark and the -346.2 meter mark on A's ruler, so that'd be at position -259.6 meters on A's ruler, and you can also see that it occurs at a time of 0 microseconds in A's frame; meanwhile, event #2 occurs at the 0.0 meter mark on A's ruler, and at a time of 1 microsecond in A's frame.

So the distance between event #1 and event #2 as measured by A is 259.6 meters, and the time between these events as measured by A is 1 microsecond, so A will conclude that the green clock had a speed of 259.6 meters/microsecond (and the speed of light is 299.792458 meters/microsecond, so that's a speed of 0.866c, which gives the correct gamma factor of 2).

But one thing is still bothering me; if all things are relative does that mean that there are no standard units by which different frames can be related?
By this, I am thinking of inertial frames with no external forces acting upon them. In such a frame, a muon's half-life, 2.2 microseconds, would surely be the same as the half-life in another inertial frame, it is a physical property, a law, and one would think, therefore, the same in any inertial frame? And I don't mean just to say it's half-life would be the same number of microseconds, I mean that the microseconds would have the same duration in any inertial frame?

All frames agree on the proper time for the muon to decay--proper time is just the time that would elapse on a clock moving along with the muon. For an object moving at constant velocity, you always can calculate the proper time between two events on its worldline by first taking the time t in your rest frame between the events and then multiplying by \sqrt{1 - v^2/c^2}. For example, if a muon is traveling at 0.6c, and I observe that it takes a time of 2.75 microseconds to decay according to clocks in my frame, then I can calculate that the proper time must have been 2.75 * sqrt(1 - 0.6^2) = 2.75 * 0.8 = 2.2 microseconds. In other frames the muon's decay time t and its velocity v will be different, but all will find that when they calculate t * sqrt(1 - v^2/c^2) they will get an answer of 2.2 microseconds.

Not sure if this answers your question, I'm still having trouble understanding what you mean by "standard units".

After all, this is something that can be reasoned/deduced from your https://www.physicsforums.com/showthread.php?t=59023"
In which you state:

This means that each ruler will observe the other one’s clocks tick exactly half as fast as their own, and will see the other ruler's distance-markings to be squashed by a factor of two.

And this could only be true if the two ruler's markings and clocks had identical (in magnitude) units.

What do you mean by "identical" in this context? If in ruler A's rest frame, ruler B's markings are only half the size of ruler A's, doesn't this mean the markings are not identical in this frame?

So, do we imply from this, that the magnitude of the units of measurement in inertial frames will be constant? That inertial units can be taken as the 'real' units and that it is these units that are 'contracted' or 'dilated' as a function of two frames relative velocity?

Again, I don't understand what you mean by "the magnitude of the units of measurement in inertial frames will be constant"...magnitude relative to what? Constant relative to what? Would it be possible to give some sort of specific physical example of what you're talking about?

If the coordinates of 'a single spacetime event' are known in frame A, the Lorentz transformation tells (an observer in) frame B what those coordinates are in frame B.
Frame C, however, can use LT to determine the coordinates of that same event from frame B (as frame B now knows what those coordinates are in frame B's coordinates).
But if frame C were then to use LT to determine what the coordinates are from those in frame A would he get the same result? I think not??

There can be no disagreement about which ruler markings/clock readings on a given frame's ruler/clock system coincide with a given event. If in frame A a lightning flash happens at x=4 light-seconds and t=0 seconds on A's ruler/clock system, and that if frame B has a velocity of +0.6c along A's x-axis, then this same flash will happen at coordinates x'=5 l.s. and t'=-3 s in B's frame. Now suppose we have a third frame C which is moving at -0.8c along A's x-axis, in the opposite direction from frame B. From the perspective of frame C, it must be true that A is moving at +0.8c along C's x''-axis, and we can use the relativistic velocity addition formula to show that from C's perspective, B must be moving at (0.8c + 0.6c)/(1 + 0.8*0.6) = 1.4c/1.48 = +0.945945...*c along C's x''-axis.

In C's frame, this same lightning flash happens at coordinates x''=6.666... l.s., and t''=5.333... s. So what happens if we start with these coordinates, and try to apply the Lorentz transformation to them to re-derive the coordinates in A's frame and B's frame? Well, for A we have a velocity of 0.8c and a gamma factor of 1.666..., so this calculation would give the coordinates in A's frame as:

x = gamma*(x'' - v*t'') = 1.666... * (6.666... - 0.8*5.333...) = 1.666... * (2.4) = 4
t = gamma*(t'' - v*x''/c^2) = 1.666... * (5.333... - 0.8*6.666...) = 0

And for B we have a velocity of 0.945945...*c and a gamma factor of 3.08333..., so this calculation would give the coordinates in B's frame as:

x' = gamma*(x'' - v*t'') = 3.08333... * (6.666... - 0.945945...*5.333...) = 3.08333... * (1.621621...) = 5
t' = gamma*(t'' - v*x''/c^2) = 3.08333... * (5.333... - 0.945945...*6.666...) = 3.08333... * (-0.972972...) = -3 s.

So, you can see that starting with the coordinates in frame C and then applying the Lorentz transformation to re-derive the coordinates in frames A and B yields the same result as starting from the coordinates in frame A and applying the Lorentz transformation to find the coordinates in frames B and C (likewise you'd get the same results if you started with the coordinates in frame B and applied the Lorentz transformation to find the coordinates in frames A and C).

 

[Grimble]

Thank you Jesse, this is great, having your help! It is clearing up a lot of points: sometimes all it needs is to see how to view or interpret what we see but I do still have a couple of queries...

Thanks for focusing on those diagrams Grimble...you ask some good questions, I'll try to address them:

Yes, but that isn't contradicted by my quote above. In the ship's own frame the clocks at the front and back of the ship are synchronized, what I said was that "for another observer who sees the ship moving", the light hits the back clock on the ship later than the light hits the front clock on the ship (as measured by 'his own network of clocks', so if he looks at the time on a clock in his network which is next to the back of the ship when the light reaches it, and compares to the time on a clock in his network which is next to the front of the ship when the light reaches it, the former time will be earlier than the latter time). So he sees the two clocks on the ship being out-of-sync, since the ship observer set them both to read the same time when the light reached them.

Yes, that certainly makes sense, I'm OK with that.

But the speed of B's green clock in A's frame is defined solely by measurements of position and time on A's own rulers and clocks, not by the time on B's clock itself. If we define event #1 as "B's green clock at the -519.3 m mark on B's ruler showing a time of 1.5 microseconds", and event #2 as "B's green clock at the -519.3 m mark on B's ruler showing a time of 2 microseconds", then if you look at the diagram you can see that event #1 occurs halfway between the -173.1 meter mark and the -346.2 meter mark on A's ruler, so that'd be at position -259.6 meters on A's ruler, and you can also see that it occurs at a time of 0 microseconds in A's frame; meanwhile, event #2 occurs at the 0.0 meter mark on A's ruler, and at a time of 1 microsecond in A's frame.

So the distance between event #1 and event #2 as measured by A is 259.6 meters, and the time between these events as measured by A is 1 microsecond, so A will conclude that the green clock had a speed of 259.6 meters/microsecond (and the speed of light is 299.792458 meters/microsecond, so that's a speed of 0.866c, which gives the correct gamma factor of 2).

Yes, but that would work out wouldn't it? For are you not merely reversing the process by which you arrived at the figures in the first place?
It seems to me, without wishing to be confrontational, that we need a separate way to verify your calculations and that we have here Einstein's system K, represented by Ruler A, and system K', represented by Ruler B?
Now, Einstein demonstrated in http://www.bartleby.com/173/11.html" that x = ct and x' = ct'.
Now, if I have worked this out correctly, when x' = {519.3} and t' = 0.5 c = \frac{519.3}{0.5} = {1038.6}

All frames agree on the proper time for the muon to decay--proper time is just the time that would elapse on a clock moving along with the muon. For an object moving at constant velocity, you always can calculate the proper time between two events on its worldline by first taking the time t in your rest frame between the events and then multiplying by \sqrt{1 - v^2/c^2}. For example, if a muon is traveling at 0.6c, and I observe that it takes a time of 2.75 microseconds to decay according to clocks in my frame, then I can calculate that the proper time must have been 2.75 * sqrt(1 - 0.6^2) = 2.75 * 0.8 = 2.2 microseconds. In other frames the muon's decay time t and its velocity v will be different, but all will find that when they calculate t * sqrt(1 - v^2/c^2) they will get an answer of 2.2 microseconds

The following was the post that introduced me to the muons;

Here is a very specific real-world test. BNL (Brookhaven Nat. Lab.) physicists stored muons with γ=29.4 in a circular ring. The muon's lifetime at rest is about 2.2 microseconds. In the ring, their lifetime was about 65 microsecons in the lab reference frame.
Bob S

So taking the proper time for the muon to decay to be 2.2 microseconds, the time in the lab rest frame to be approximately 65 microseconds and γ = 29.4 that fits.
This comes close to answering what bothers me; my difficulty is, I suppose, that so many contributors seem to be very reluctant to commit themselves to definite statements and this has led to much confusion.

Not sure if this answers your question, I'm still having trouble understanding what you mean by "standard units".

Let me try to simplify my question. There is a lot of talk of 'seconds', 'microseconds', 'proper time' and 'coordinate time' but there is some confusion in my mind about what is being referred to.

It seems to me that proper time is as you defined it above:
coordinate time is that same proper time but transformed, as you would measure it in your rest frame.
The tricky question is what scales are the different seconds measured upon?
Let me put it this way, if two separate inertial frames A & B are moving with the same speed relative to a third frame C, and let us say that 0.866c is that relative velocity, giving us a gamma factor of 2, as in your example above.
Then the C will measure the seconds in each of the other two frames, moving at the same relative velocity, as being half as long as the proper seconds in A and B.
Now my question is, in frame C will the transformed seconds from A equal those transformed from B? i.e. are the proper seconds in A equal in magnitude to the proper seconds in B?
One would assume so from the way your Rulers are drawn in your example.

I'm sorry if this seems like questioning the obvious but so many times in these threads do we find someone coming in with statements like 'but those seconds are in different frames so you can't compare them' – or am I just becoming paranoid?

What do you mean by "identical" in this context? If in ruler A's rest frame, ruler B's markings are only half the size of ruler A's, doesn't this mean the markings are not identical in this frame?

So here again I use identical to compare the proper units in the two frames; i.e. are the proper units of one ruler, in its frame, equal in magnitude to the proper units of the other ruler, in its frame?
(that is if they were being compared by another frame moving with the same relative velocity to each of those frames) – Sorry for going on so much, but I am trying to be explicit so we both understand what I am saying.

So, you can see that starting with the coordinates in frame C and then applying the Lorentz transformation to re-derive the coordinates in frames A and B yields the same result as starting from the coordinates in frame A and applying the Lorentz transformation to find the coordinates in frames B and C (likewise you'd get the same results if you started with the coordinates in frame B and applied the Lorentz transformation to find the coordinates in frames A and C).

Yes, of course! I had forgotten to use the relative velocity addition formula

Grimble