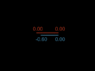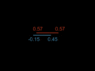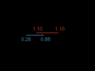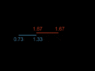Exploring the Paradox of Relative Truth in Special Relativity

[name123]

There are 2 aspects to this: acceleration profile, and clock resynchronization.
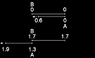
1. You need to understand that it is different whether the train accelerates at once along its length in a) the original (track) frame, or b) in the moving frame. Assuming both acceleration and deceleration are simultaneous in the track frame, every car/sausage spent the same time moving, so the offset will be the same.
If it starts in the track frame but stops in the train frame, the front of the train will be moving longer and the clock will be more behind.
In your sausage spaceship, it's not clear which, if any of these 2 ways, you are imagining.

With the example I gave with the "sausage" spaceship and the "pastry" spaceship, there is only the acceleration to bring one of the spaceships into the rest frame of the other to compare clocks (after the 100 minutes on the clock of whichever spaceship undergoes the acceleration for example).

So It is not like the train example where the train undergoes 2 accelerations in different directions (one to accelerate and one to decelerate).

2. Let's say there is the driver in front and the conductor in the back. Just after acceleration, will the conductor think "hmm we should start moving any minute now" while the driver thinks "we've been moving for hours now"? Nope. Their clocks are simply out of sync, but they agree they've just started moving. If they stop soon, they don't need to bother resyncing their clocks in the moving frame.

You can compute the time elapsed on any of the clocks, but if they resynchronize, don't be surprised you get surprising/different results along the train/ship.

So in the "sausage" spaceship and the "pastry" spaceship example the clocks on each can be considered to be in synch, and both can calculate when they would be passing the designated clock on the other ship, and choose that time reset their clocks (along each spaceship). So one spaceship will reset their clocks at time x in their frame of reference, and the other will reset their clocks at time y in their frame of reference such that when the 2 appointed clocks pass they will see each others time as 0. Does the scenario now seem clear?

 

[jbriggs444]

With the example I gave with the "sausage" spaceship and the "pastry" spaceship, there is only the acceleration to bring one of the spaceships into the rest frame of the other to compare clocks (after the 100 minutes on the clock of whichever spaceship undergoes the acceleration for example).

Even if you accelerate only once, you will still mess up the clocks according to at least one of the frames involved.

 

[name123]

Even if you accelerate only once, you will still mess up the clocks according to at least one of the frames involved.

Yes, but the point is what would the clocks read if after 100 minutes after the reset according to the "sausage" spaceship, the "sausage" spaceship accelerated to the "pastry" spaceship frame of reference, and what would the clocks read if after 100 minutes after the reset according to the "sausage" spaceship, the "pastry" spaceship accelerated to the "sausage" spaceship frame of reference?

 

[Janus]

Sorry for the delay in response by the way.Regarding the clocks all over the train appearing slower than the ones on the track if it stopped. I don't quite understand. To highlight the point consider again the 2 long spaceships passing at 0.6v, both being long, say 10 light years each, and one passing through the middle of the other in a way analogous to a sausage roll. One spaceship being like the sausage one like the pastry. As a clock in the middle of the "sausage" spaceship roughly passes a clock in the middle of the "roll" spaceship , the clocks on each set themselves to zero and are synchronised on each (though not across spaceships). One can imagine the "pastry" ship being analogous to the track in the scenario you gave. The problem with the clocks all over the "sausage" spaceship showing 0.8 the amount of time that the clocks on the "pastry" spaceship showed, supposing 100 minutes had passed, that would seem to imply that the "sausage" spaceship clocks would be showing only 80 minutes had passed, if the "sausage" spaceship underwent an acceleration that placed it at rest with the "pastry" spaceship. But what if the "pastry" spaceship had undergone an acceleration that placed it at rest with the "sausage" spaceship?

Clocks according to "Sausage" and "Roll", according to each when their midpoints pass and each sync their clocks to zero.
Top is for the rest frame of the "sausage", bottom is for the rest frame of the "roll" . Thin cylinder is the sausage and thick transparent one is the roll. Numbers are rounded to the nearest 1/10.

A bit later, when the midpoint clock of the sausage meets the clock just to the left of midpoint ( as shown in the image). Again top is sausage frame, bottom is roll frame.

Sausage frame: Clock in roll starts 0.8 ly away, and thus takes 1.3333 yrs to reach the midpoint clock by the sausage clocks.. It ticks off 1.3333 x 0.8 = 1.06667 yr during that time. when it started it already read 0.6 years, thus it reads 1.6667 years upon arriving at the sausage midpoint.

Roll frame. Sausage midpoint clock starts reading zero and 0.8 ly away. It take 1.6667 years to reach the Roll's clock and ticks off 1.3333 years in doing so.

Thus both frame agree as to what the clocks read when they meet. This works out to be true for any pair of clocks.

As to what happens if either undergoes acceleration until they are at rest with respect to each other:
If the sausage undergoes acceleration, then It will measure the Roll as growing in length and its clocks as matching each other in synchronizing. It will measure its own clock as going out of sync with each other.
The roll will measure nothing happening to itself or its clocks, but will measure the sausage as growing in length and its clocks going even further out of sync. At the end both will agree that the roll clocks are in sync, while the Sausage clocks aren't. they also would both agree as to the respective readings of any two clocks that end up next to each other.

The reverse happens if it is the Roll that accelerates, the roll clocks will end up out of sync and the sausage clocks will be in sync.

The upshot is that which of the two undergoes the acceleration does make a difference in the outcome, but both will agree as to what that end result would be.

 

[SlowThinker]

With the example I gave with the "sausage" spaceship and the "pastry" spaceship, there is only the acceleration to bring one of the spaceships into the rest frame of the other to compare clocks

OK so if we ignore the tear/crush issues, the clock can be stopped during acceleration because the time spent accelerating is negligible.
In the scenario where the train goes for 1 track-second at 0.6c, the train clock will reach 0.8s wherever they are.
In the sausage/roll scenario, if the sausage's clock all over the ship before turnaround are showing the same time as viewed by its crew, they will be showing different times after turnaround. Even though they are showing the same time as before the turnaround.

So in the "sausage" spaceship and the "pastry" spaceship example the clocks on each can be considered to be in synch, and both can calculate when they would be passing the designated clock on the other ship, and choose that time reset their clocks (along each spaceship). So one spaceship will reset their clocks at time x in their frame of reference, and the other will reset their clocks at time y in their frame of reference such that when the 2 appointed clocks pass they will see each others time as 0. Does the scenario now seem clear?

Not sure. You can do it for one clock on each ship, but if you do it all along its length, the clock on the same ship will be showing different times.
If you only do it for the central clock and set others on each ship according to the central clock, you don't even need to accelerate the ships. You can simply make a photo of the sausage ship's clock through its windows from the roll ship, to see that they are off.

Can you repeat which issues seem unclear as of now?

 

[Dale]

I think I am going to go eat sausage for breakfast!

Edit: I toasted a croissant for a roll too. Yum!

 

[name123]

Sausage frame: Clock in roll starts 0.8 ly away, and thus takes 1.3333 yrs to reach the midpoint clock by the sausage clocks.. It ticks off 1.3333 x 0.8 = 1.06667 yr during that time. when it started it already read 0.6 years, thus it reads 1.6667 years upon arriving at the sausage midpoint.

Roll frame. Sausage midpoint clock starts reading zero and 0.8 ly away. It take 1.6667 years to reach the Roll's clock and ticks off 1.3333 years in doing so.

Thus both frame agree as to what the clocks read when they meet. This works out to be true for any pair of clocks.

Not sure why there is any asymmetry. In your second diagram why it appears different to the "sausage" than it does to the "roll".

As to what happens if either undergoes acceleration until they are at rest with respect to each other:
If the sausage undergoes acceleration, then It will measure the Roll as growing in length and its clocks as matching each other in synchronizing. It will measure its own clock as going out of sync with each other.
The roll will measure nothing happening to itself or its clocks, but will measure the sausage as growing in length and its clocks going even further out of sync. At the end both will agree that the roll clocks are in sync, while the Sausage clocks aren't. they also would both agree as to the respective readings of any two clocks that end up next to each other.

The reverse happens if it is the Roll that accelerates, the roll clocks will end up out of sync and the sausage clocks will be in sync.

The upshot is that which of the two undergoes the acceleration does make a difference in the outcome, but both will agree as to what that end result would be.

What about the two clocks that passed each other when both were 0. Will they show the same time, or will it matter which underwent the acceleration to be at rest with the other? If the latter then does the interval between when they were set to 0 and the acceleration?

Also with the earlier scenario where it was a track and a 10 light year long train where all the clocks are synchronised and then the train accelerates to then travel at 0.6v for one second then decelerates to be back at rest with the track. What would the observers on the front and end of the train be considering the clocks on the track to be stating before the train stopped?

 

[name123]

Not sure. You can do it for one clock on each ship, but if you do it all along its length, the clock on the same ship will be showing different times.
If you only do it for the central clock and set others on each ship according to the central clock, you don't even need to accelerate the ships. You can simply make a photo of the sausage ship's clock through its windows from the roll ship, to see that they are off.

Can you repeat which issues seem unclear as of now?

The scenario seems clear to me, but what I am not sure about is if the central clocks were coloured red and all other clocks green, then when the "sausage" ship's red clock shows 100 minutes, what will the other ship's red clock be showing according to the "sausage" ship, and if one of the ships then accelerates to the others frame of reference, what difference does it make to the time found to be on the "pastry" ship's red clock which one did the accelerating?

Edit: Also with the acceleration, it can be assumed whether with a train or a spaceship that they are made up of multiple linked segments each with their own engine or thrusters. So no need to imagine the effect of a single engine propagating over a long object.

 

[Janus]

Not sure why there is any asymmetry. In your second diagram why it appears different to the "sausage" than it does to the "roll".

Call the clock on the Roll B and the One on the sausage A. Both scenarios start when the midpoint clocks are adjacent and read zero.
So, in the sausage frame we start like the top diagram and end as the bottom diagram.

The distance between Clock A and B is the same as the distance between Clock B and the roll midpoint clock. This is 1 ly in the roll frame, but length contracted to 0.8 ly in the sausage frame As B moves to the left to meet with A, A advances 1.3 yrs and B advances 1.1 yrs.

In the roll frame:

We still start as the midpoint clocks meet and read zero. But now, the distance between A and B is the distance between B and the roll midpoint clock as measured in the Roll frame and is 1ly. As A moves to the left to meet up with A, it takes 1.7 yrs according to the clock in the Roll frame and The sausage clocks tick off 1.3 years in that same time.

What about the two clocks that passed each other when both were 0. Will they show the same time, or will it matter which underwent the acceleration to be at rest with the other? If the latter then does the interval between when they were set to 0 and the acceleration?

There are some specifics missing here that would allow for an answer. If two clocks are right next to each other when one of them accelerates, and the acceleration is high enough that they don't move significantly with respect to each other during the acceleration ( in other words they are still right next to each other after the acceleration) then they will have the same time on them before and after. (Of course there will always some[i/] small displacement during the accleration.)

Also with the earlier scenario where it was a track and a 10 light year long train where all the clocks are synchronised and then the train accelerates to then travel at 0.6v for one second then decelerates to be back at rest with the track. What would the observers on the front and end of the train be considering the clocks on the track to be stating before the train stopped?

Again, once you accelerate the train, all the clocks on the train will go out of sync with each other as measured by the train, as will the clocks on the tracks. A the moment before the deceleration starts, an observer on the train will measure clocks on the tracks in front of him as being ahead in terms of time of the clock he is beside and those behind him.
So let's say you are in the front of the train. At that moment, you and the train is at rest with respect to the tracks, and your clock reads zero as do all the clock on the train and all the clocks on the tracks. You accelerate over an infinitesimal period of time to 0.6 c, so that you clock and the clock you were next to on the tracks for all practical purposes still read zero and are still next to each other. The clocks behind you on the tracks will be now reading less than zero and those in front as reading greater than zero (you won't actually see this, because of light signal delay). The difference in clocks will be 0.6 s for every 0.8 light sec away from you that any clock is.
You keep this up for 1 sec by your clock, during which time the clocks on the tracks advance 0.8 sec. The clock that you pass after that 1 sec will read 1.25 sec. ( its will have advanced by 0.8 sec during your 1sec, but was already reading 0.45 sec at the beginning of your 1 sec. A clock 0.8 light sec ahead of you on the track will read 1.85 sec, while one behind you will read 0.65 sec. Other track clocks will differ depending on their position on the tracks.

 

[name123]

Call the clock on the Roll B and the One on the sausage A. Both scenarios start when the midpoint clocks are adjacent and read zero.
So, in the sausage frame we start like the top diagram and end as the bottom diagram.
View attachment 229259

The distance between Clock A and B is the same as the distance between Clock B and the roll midpoint clock. This is 1 ly in the roll frame, but length contracted to 0.8 ly in the sausage frame As B moves to the left to meet with A, A advances 1.3 yrs and B advances 1.1 yrs.

In the roll frame:
View attachment 229258

We still start as the midpoint clocks meet and read zero. But now, the distance between A and B is the distance between B and the roll midpoint clock as measured in the Roll frame and is 1ly. As A moves to the left to meet up with A, it takes 1.7 yrs according to the clock in the Roll frame and The sausage clocks tick off 1.3 years in that same time.

Still not getting it. The top of each of the diagrams seems symmetrical but the bottoms seem different, and I am not sure why given the symmetry of their top. It seems like you are suggesting it makes a difference which is the "sausage" and which is the "roll". Is that what you are suggesting?

There are some specifics missing here that would allow for an answer. If two clocks are right next to each other when one of them accelerates, and the acceleration is high enough that they don't move significantly with respect to each other during the acceleration ( in other words they are still right next to each other after the acceleration) then they will have the same time on them before and after. (Of course there will always some[i/] small displacement during the accleration.)

I am fine with the time dilation due to acceleration being proportional to the amount of time at a given acceleration thus as the time spent accelerating tends to 0 the time dilation due to it tends to 0. What I am not clear about is that if the central clocks were coloured red and all other clocks green, then when the "sausage" ship's red clock shows 100 minutes, what will the other ship's red clock be showing according to the "sausage" ship, and if one of the ships then accelerates to the others frame of reference, what difference does it make to the time found to be on the "pastry" ship's red clock which one did the accelerating?

Again, once you accelerate the train, all the clocks on the train will go out of sync with each other as measured by the train, as will the clocks on the tracks. A the moment before the deceleration starts, an observer on the train will measure clocks on the tracks in front of him as being ahead in terms of time of the clock he is beside and those behind him.
So let's say you are in the front of the train. At that moment, you and the train is at rest with respect to the tracks, and your clock reads zero as do all the clock on the train and all the clocks on the tracks. You accelerate over an infinitesimal period of time to 0.6 c, so that you clock and the clock you were next to on the tracks for all practical purposes still read zero and are still next to each other. The clocks behind you on the tracks will be now reading less than zero and those in front as reading greater than zero (you won't actually see this, because of light signal delay). The difference in clocks will be 0.6 s for every 0.8 light sec away from you that any clock is.
You keep this up for 1 sec by your clock, during which time the clocks on the tracks advance 0.8 sec. The clock that you pass after that 1 sec will read 1.25 sec. ( its will have advanced by 0.8 sec during your 1sec, but was already reading 0.45 sec at the beginning of your 1 sec. A clock 0.8 light sec ahead of you on the track will read 1.85 sec, while one behind you will read 0.65 sec. Other track clocks will differ depending on their position on the tracks.

Sorry still not quite clear, I could guess at the calculation but it would be useful if you did it (if you don't mind), with the
10 light year long train where all the clocks are synchronised and then the train accelerates to then travel at 0.6v for one second then decelerates to be back at rest with the track. What would the observers on the front and end of the train be considering the clocks on the track to be stating before the train stopped? The reason I ask is that it seems from your answer that the observer at the end of the train would be thinking that the clock on the track was showing a time prior to the clocks being set to 0. I perhaps have misunderstood.

Edit: Changed the last sentence from:

The reason I ask is that it seems from your answer that the observer at the end of the train would be thinking that the clock on the train was showing a time prior to the clocks being set to 0. I perhaps have misunderstood.

to:

The reason I ask is that it seems from your answer that the observer at the end of the train would be thinking that the clock on the track was showing a time prior to the clocks being set to 0. I perhaps have misunderstood.

 

[SlowThinker]

if the central clocks were coloured red and all other clocks green, then when the "sausage" ship's red clock shows 100 minutes, what will the other ship's red clock be showing according to the "sausage" ship

If the relative speed is 0.6c, it will show 80 minutes.

and if one of the ships then accelerates to the others frame of reference, what difference does it make to the time found to be on the "pastry" ship's red clock which one did the accelerating?

If the pastry ship accelerated to the sausage frame, and the process was quick enough, the clock will still show 80 minutes. The clock won't just skip time when you are next to it. It only happens in the distance.
If it was the Sausage accelerating, you'd have to first ask "according to the Pastry, what do their clock show when the Sausage clocks show 100 minutes?" It's not 80 minutes but 125.

Edit: Also with the acceleration, it can be assumed whether with a train or a spaceship that they are made up of multiple linked segments each with their own engine or thrusters. So no need to imagine the effect of a single engine propagating over a long object.

Even then the links can be fired at different times. In fact, they always will be fired at different times from someone's perspective.

 

[name123]

If the pastry ship accelerated to the sausage frame, and the process was quick enough, the clock will still show 80 minutes. The clock won't just skip time when you are next to it. It only happens in the distance.
If it was the Sausage accelerating, you'd have to first ask "according to the Pastry, what do their clock show when the Sausage clocks show 100 minutes?" It's not 80 minutes but 125.

So when the red clock on the "sausage" ship frame of reference is showing 100 there is a near instantaneous acceleration into one frame of reference or the other the time on the "pastry" ship red clock will vary from 80 minutes to 125 minutes depending on which did the accelerating.

I must admit I find this confusing.

Because say the clocks on the ship were separated by a distance of a light second each according to each ship's own frame of reference; the clock on the "pastry" ship that had last passed the "sausage" ship's red clock showing 100 minutes could be known as the "pastry" ship's blue clock. Presumably they would agree on the time each was showing as they passed. Likewise on the "sausage" ship the blue clock could be the clock that last passed the "pastry" ship's red clock before the acceleration (it would presumably, from the frame of reference the "sausage" ship, also be showing 100 minutes prior to acceleration). Presumably they would both agree on what respective time each was showing as they passed. From what you wrote I assume the red clock on the "pastry" ship would be showing 80 minutes as it passed the "sausage" ship's blue clock. Yet when the "sausage" ship near instantaneously accelerates to be at rest with the pastry ship, the "pastry" ship's red clock will not show 80 minutes but 125 minutes. Will the "sausage" ship's blue clock still be showing 100 minutes at that point? And how does the time on the "pastry" ship's red clock not seem to jump to the "sausage" ship's blue clock? As the "pastry" ship's red clock was passing the "sausage" ship's blue clock was it not be showing 80 minutes then as the "sausage" ships blue clock seemed to instantaneously accelerate into rest with it, the "pastry" ship's red clock time changed to showing 125 minutes?

Edit: I assume I have made a mistake here, and that from the "pastry" ships frame of reference, it's red clock would be showing 80 minutes, the "sausage" ship's blue clock would be showing 100 minutes, and the "sausage" ship's red clock would be showing something like 64 minutes and hadn't yet started the acceleration, and that by the time it did, the "pastry" ships red clock was showing 125 minutes.

 

[SlowThinker]

So when the red clock on the "sausage" ship frame of reference is showing 100 there is a near instantaneous acceleration into one frame of reference or the other the time on the "pastry" ship red clock will vary from 80 minutes to 125 minutes depending on which did the accelerating.

I must admit I find this confusing.

Yes. There is no "when". There is "as seen from Pastry when" and "as seen from Sausage when", and they're different, and it also depends on position.

The acceleration doesn't move the clock, it just moves the perspective.

 

[name123]

Yes. There is no "when". There is "as seen from Pastry when" and "as seen from Sausage when", and they're different, and it also depends on position.

The acceleration doesn't move the clock, it just moves the perspective.

So what about the situation where the "sausage" spaceship is at rest with the "pastry" spaceship, and they all synchronous their clocks and reset to 0, and then the "sausage" spaceship then accelerates to 0.6v for one second, and then accelerates back to the rest frame of the pastry spaceship.

You can imagine the "sausage" spaceship to be segmented, and for each segment to have its own rockets, and for them to start the moment the clocks reset to 0. Presumably the observers on the "pastry" spaceship will all agree the segments all set off at the same time. Would the observers on the "pastry" spaceship all agree the segments reached 0.6v at the same time? If so would they all agree what the clocks of those segments read when they reached it? Also after the "sausage" spaceship which we can assume is 10 light years long has been going (according to it's frame of reference) for one second what roughly would the observers on the front and end of it think the last "pastry" spaceship clock each had passed was showing on its clock (imagine the "pastry" spaceship to be considerably longer than the "sausage" one)?

 

[Janus]

Still not getting it. The top of each of the diagrams seems symmetrical but the bottoms seem different, and I am not sure why given the symmetry of their top. It seems like you are suggesting it makes a difference which is the "sausage" and which is the "roll". Is that what you are suggesting?

Each image is a set of diagrams showing two different times: When the "midpoint" clocks meet and both read zero, and then later when the "sausage" midpoint clock meets the next clock Left of the midpoint clock of the "pastry". So I don't see where you get any asymmetry begin the top and bottom diagrams in each image.
Maybe animations will help:
The pastry is the red line and its clocks are the red ones, blue represents the sausage and its clocks. Both the pastry and sausage measure their own clocks as being 1 ly apart and their clocks synchronized to each other. The starting moment in each animation is when two clocks, each reading zero pass each other. I'll limit the animation to just two clocks in each frame to keep things simpler.

First the pastry frame:

The rightmost clocks both start at zero. The sausage and its clocks move to the left at 0.6c until its rightmost clock aligns with the leftmost pastry clock. We pasuse to compare clocks. The sausage clocks are closer together than the pastry clocks because the pastry is length contracted. The left sausage clock reads 0.6 sec before the right one due to the relativity of simultaneity. (though this clock doesn't have an active roll in this situation.). Both sausage clocks tick 0.8 as fast as the pastry clocks due to time dilation.

Now the sausage frame. Note that we have not changed anything about the scenario, we are just switching the frame from which we are making the observations.

Both right clocks still start at zero. But in this frame, it is the pastry that is in motion (left to right), and undergoes length contraction and whose clocks undergo time dilation and are effected by the relativity of simultaneity. Thus the left pastry clock starts with a reading of 0.6 yrs, and starts only 0.8 ly from the right sausage clock.
Thus it only takes 1.33 yrs for the right sausage clock and left pastry clock to meet. During which time, the pastry clocks run at a rate 0.8 that of the sausage clocks and advance 1.07 years, and since the left pastry clock started at 0.6 years, it reads 1.67 years upon reaching the right sausage clock.

I am fine with the time dilation due to acceleration being proportional to the amount of time at a given acceleration thus as the time spent accelerating tends to 0 the time dilation due to it tends to 0. What I am not clear about is that if the central clocks were coloured red and all other clocks green, then when the "sausage" ship's red clock shows 100 minutes, what will the other ship's red clock be showing according to the "sausage" ship, and if one of the ships then accelerates to the others frame of reference, what difference does it make to the time found to be on the "pastry" ship's red clock which one did the accelerating?

After 100 minutes by the sausage clock, the pastry red clock will read 80 min. ( and be 60 light min away) according to the sausage. If The sausage clock then suddenly accelerates to come to rest with respect to the pastry, then the red pastry clock will jump to read 125 min, after they have come to rest with respect to each other.
If the sausage clock accelerates, first you have to decide "when" it accelerates. Does it accelerate when it reads 80 min and is 48 light min from the sausage clock ( and according to it, the sausage clock reads 64 min), or does it accelerate when the sausage clock read 100 minutes according to the pastry, and the pastry clock reads 125 min and is 75 light min from the sausage clock.
In the first case, it will still read 80 min after acceleration and the pastry clock will jump to 100 min.
In the second case, it will still read 125 min, and the sausage clock jumps to 156 min.

Sorry still not quite clear, I could guess at the calculation but it would be useful if you did it (if you don't mind), with the
10 light year long train where all the clocks are synchronised and then the train accelerates to then travel at 0.6v for one second then decelerates to be back at rest with the track. What would the observers on the front and end of the train be considering the clocks on the track to be stating before the train stopped? The reason I ask is that it seems from your answer that the observer at the end of the train would be thinking that the clock on the track was showing a time prior to the clocks being set to 0. I perhaps have misunderstood.

Edit: Changed the last sentence from:

The reason I ask is that it seems from your answer that the observer at the end of the train would be thinking that the clock on the train was showing a time prior to the clocks being set to 0. I perhaps have misunderstood.

to:

The reason I ask is that it seems from your answer that the observer at the end of the train would be thinking that the clock on the track was showing a time prior to the clocks being set to 0. I perhaps have misunderstood.

Whenever you start discussing acceleration and extended objects in relativity it can be very complicated. For example, there is something called the Rindler horizon, which limits what events an accelerating observer can measure in the direction opposite of his acceleration. The higher the acceleration, the closer to the observer, the Rindler horizon is. Now, In this scenario, where one is trying to limit the time of acceleration to an extremely short period, you have to assume an extremely high acceleration, and basically a Rindler horizon that, in effect, does not allow you to detect anything happening "behind" you.
To illustrate just how complex this subject is, here is a paper on the Rindler Horizon and its effects in different situations.
http://www.gregegan.net/SCIENCE/Rindler/RindlerHorizon.html

Now obviously, if the clocks weren't set and started from zero until the train started its initial acceleration, then the train observer would never say that they read less than zero. However, if we assume that the track clocks had been running in sync with each other and counting up from negative readings to zero until the train accelerated, then the train observer, could say that some given moment after it reached 0.6 relative to the tracks, that some of the track clocks had not yet read 0 (again taking to account the Rindler horizon)

In all honesty, I would forgo tying to examine scenarios which involve extended objects and acceleration until you have a much greater grasp on those which deal strictly with inertial motion. Adding accelerations at this point will not make things clearer.

 

[Janus]

So what about the situation where the "sausage" spaceship is at rest with the "pastry" spaceship, and they all synchronous their clocks and reset to 0, and then the "sausage" spaceship then accelerates to 0.6v for one second, and then accelerates back to the rest frame of the pastry spaceship.

You can imagine the "sausage" spaceship to be segmented, and for each segment to have its own rockets, and for them to start the moment the clocks reset to 0. Presumably the observers on the "pastry" spaceship will all agree the segments all set off at the same time. Would the observers on the "pastry" spaceship all agree the segments reached 0.6v at the same time? If so would they all agree what the clocks of those segments read when they reached it? Also after the "sausage" spaceship which we can assume is 10 light years long has been going (according to it's frame of reference) for one second what roughly would the observers on the front and end of it think the last "pastry" spaceship clock each had passed was showing on its clock (imagine the "pastry" spaceship to be considerably longer than the "sausage" one)?

This is a lot more complicated than it seems. If you arranged things so that in the sausage frame, the spacing between segments remained constant and all the segments started and stopped accelerating at the same moment, then according to the pastry ship, the segments and thus the distance between them was shrinking due to length contraction during this whole acceleration. But this also means that, at any given moment the Leading segment was traveling at a lower speed relative to the rear segment and thus its clock was exhibiting a greater time dilation rate. In other words, according to the pastry ship, the clocks in the segments wouldn't be ticking at the same rate.
In addition, due to the fact that the rest frame of the sausage ship is a non-inertial one, anyone on the sausage ship would say that clocks at the trailing segment would be running slower than those in the leading segment. Thus, for each segment to stop its acceleration " at the same time" across the ship, each segment would have to stop its acceleration at a different time according to its own clock. So first you would have to work out the end difference between clocks of the sausage ship as measured in the sausage ship, and then apply the relativity of simultaneity to make comparisons between clocks of the relatively moving frames.
Working with extended bodies under acceleration is not a simple problem in Relativity.

 

[SlowThinker]

So what about the situation where the "sausage" spaceship is at rest with the "pastry" spaceship, and they all synchronous their clocks and reset to 0, and then the "sausage" spaceship then accelerates to 0.6v for one second, and then accelerates back to the rest frame of the pastry spaceship.

You can imagine the "sausage" spaceship to be segmented, and for each segment to have its own rockets, and for them to start the moment the clocks reset to 0. Presumably the observers on the "pastry" spaceship will all agree the segments all set off at the same time.

In this scenario yes, but it can be confusing to mix these 2 scenarios. You can refer to it as the train&track.

Would the observers on the "pastry" spaceship all agree the segments reached 0.6v at the same time?

Yes, at time just above 0 as we assume the acceleration to be fast.

If so would they all agree what the clocks of those segments read when they reached it?

Yes, just a bit above 0. But the Sausage's crew would say that for a second the clocks along the Sausage were showing different times - but each crewman would think that their nearest clock is the right one.

Also after the "sausage" spaceship which we can assume is 10 light years long has been going (according to it's frame of reference) for one second what roughly would the observers on the front and end of it think the last "pastry" spaceship clock each had passed was showing on its clock (imagine the "pastry" spaceship to be considerably longer than the "sausage" one)?

This sentence doesn't seem to make sense.
Each Sausage crewman would see the nearest Pastry clocks to slow down, they'd move to clocks that were already a bit in the future (clocks jumped during acceleration), and then the Pastry's clock start going at normal speed. This whole process in total would move Pastry's clock 1.25 seconds into the future (while only 1 second has passed for the Sausage crew).

 

[name123]

Each image is a set of diagrams showing two different times: When the "midpoint" clocks meet and both read zero, and then later when the "sausage" midpoint clock meets the next clock Left of the midpoint clock of the "pastry". So I don't see where you get any asymmetry begin the top and bottom diagrams in each image.

Sorry for the late reply.

What I am slightly confused about is why in one frame of reference the moving clock reads 1.67 when it passes the next clock along, and in the other it reads 1.33. You seem to be applying a 0.8 time dilation from one frame of reference and not the other, and I am not sure why given the seeming symmetry of the situation.

Now obviously, if the clocks weren't set and started from zero until the train started its initial acceleration, then the train observer would never say that they read less than zero. However, if we assume that the track clocks had been running in sync with each other and counting up from negative readings to zero until the train accelerated, then the train observer, could say that some given moment after it reached 0.6 relative to the tracks, that some of the track clocks had not yet read 0 (again taking to account the Rindler horizon)

What if the clocks showed 999 before the event of being set to 0 which was immediately followed by the event of the train accelerating? In such a case no clock showing 999 would be observed post the acceleration event I assume.

 

[name123]

This is a lot more complicated than it seems. If you arranged things so that in the sausage frame, the spacing between segments remained constant and all the segments started and stopped accelerating at the same moment, then according to the pastry ship, the segments and thus the distance between them was shrinking due to length contraction during this whole acceleration. But this also means that, at any given moment the Leading segment was traveling at a lower speed relative to the rear segment and thus its clock was exhibiting a greater time dilation rate. In other words, according to the pastry ship, the clocks in the segments wouldn't be ticking at the same rate.

This seems quite strange. You seem to be stating that from the pastry ships perspective the rate of acceleration of a segment that used its own rockets to propel would depend upon whether it was connected to other segments. If instead of a sausage ship there were two independent segments. One where the rear segment of the sausage ship would have been, and one where the front segment of the sausage ship would have been. Would the front one still appear to be moving slower than the rear one? That the engineers on the pastry ship when calculating the speed of an accelerating segment would have to take into account where it took off from?

 

[name123]

This sentence doesn't seem to make sense.
Each Sausage crewman would see the nearest Pastry clocks to slow down, they'd move to clocks that were already a bit in the future (clocks jumped during acceleration), and then the Pastry's clock start going at normal speed. This whole process in total would move Pastry's clock 1.25 seconds into the future (while only 1 second has passed for the Sausage crew).

So the sausage ship and pastry ship synch their clocks and set them to 0. Then the segmented sausage ship accelerates to 0.6v and maintains that velocity for 1 second. At that point what roughly would the observers on the front and end of the sausage ship think the last "pastry" spaceship clock each had passed was showing on its clock (imagine the "pastry" spaceship to be considerably longer than the "sausage" one)? I had assumed that they would not both report the same time on the last "pastry" spaceship clock they passed, as I had assumed they would not just think the "pastry" spaceship clocks were slower, but also out of synch.

 

[SlowThinker]

At that point what roughly would the observers on the front and end of the sausage ship think the last "pastry" spaceship clock each had passed was showing on its clock?

The Sausage crew would see the newly nearest Pastry clock as all showing 1.00s. Their own wristwatch would show 0.80s. However if the crew in the front and in the back of Sausage compared their wristwatches, they could be hours off. Obviously the Pastry clocks would be off by the same amount AND 0.20s ahead.
The Pastry's clock nearest at the time of start would now be 0.6 light seconds away and showing 0.80s.

If the Sausage crew resynchronized the clocks after the start, that needs to be said explicitly.

 

[Janus]

Sorry for the late reply.

What I am slightly confused about is why in one frame of reference the moving clock reads 1.67 when it passes the next clock along, and in the other it reads 1.33. You seem to be applying a 0.8 time dilation from one frame of reference and not the other, and I am not sure why given the seeming symmetry of the situation.

We are not considering how long it takes for a clock to move from one clock to the next in each frame according to that frame. For instance, if clock C of the pastry is next to clock A of the sausage, it will measure 1.33 yrs until clock B of the sausage reaches it. Just like in our example clock A for the sausage measures 1.33 yrs unitl clock B of the pastry reaches it. But when comparing the two scenarios above, there is no common moment between the two frames that both frame will agree on.

In the example we are working with we are starting from a common moment that both frames agree on (the passing of two clocks when they both read zero.)
And this moment looks like this in the two frames. ( I just noticed something here that might have added to your confusion. In my last version of these images, I forgot the minus sign in front of the 0.6 shown in the bottom diagram.) I further labeled two other clocks as C and D. :

The top diagram is this moment according to the sausage and the bottom is the same moment according to the pastry.
In both frames clock A of the sausage is passing a pastry clock D as it reads zero.
According to sausage frame clock B has already passed clock C on its way to its meeting with clock A, However according to the pastry frame, Clock C has yet to meet up with clock B. If we were rewind the top image back to when B is next to C, then clock C will read -0.2/.6 = -0.333...yrs, and clock B will read 0.6- (0.333...x 0.8) =0.333...yr.
Likewise, if you run the bottom diagram forward until C meets B, then B reads 0.2/0.6 = 0.333... yrs and C reads -.6+(0.333...x 0.8) = -0.333... yrs
Thus both frames agree as to what C and B read as they pass each other. But B passing C is not the same moment as A passing D in either frame.

In the sausage frame, it occurrs before[ A and D pass each other, when A reads -0.333... yrs and D reads -2.666... yrs.
In the pastry frame, B and C meet after A and D pass each other, when D reads 0.333... yrs and A reads 2.666... yrs.
All a result of time dilation, length contraction and the relativity of simultaneity working in concert.
Again, you need to pick one moment that both frames agree upon (such as clocks A and D passing each other) and then work from that moment in both frames.
To supply the symmetry you seem to feel is lacking, you could add two more clocks to the example above: clock F which is a pastry clock to the right of clock D and clock E which is a sausage clock to the right of clock A. Then if you consider what time reads on clock F when it meets clock E you get 1.333... yrs, (the same as clock A reads when it meets clock B), and you get 1.666... yrs for the time on clock E when it meets clock F ( the same reading as clock B reads when it meets clock A)

What if the clocks showed 999 before the event of being set to 0 which was immediately followed by the event of the train accelerating? In such a case no clock showing 999 would be observed post the acceleration event I assume.

Without actual numbers, magnitude and duration of acceleration etc, you can't arrive at an exact answer as what any given observer would see.

 

[Janus]

This seems quite strange. You seem to be stating that from the pastry ships perspective the rate of acceleration of a segment that used its own rockets to propel would depend upon whether it was connected to other segments. If instead of a sausage ship there were two independent segments. One where the rear segment of the sausage ship would have been, and one where the front segment of the sausage ship would have been. Would the front one still appear to be moving slower than the rear one? That the engineers on the pastry ship when calculating the speed of an accelerating segment would have to take into account where it took off from?

Any connection between the segments is not relevant.
Take two ships, one behind the other. Both are accelerating such that, as measured by each ship, the distance between their ship and the other ship remains fixed, and the relative speed between them is zero. They will observe each others clocks as running at different rates, with the lead ship's clock running faster.
It is the frame that they are accelerating with respect to that would measure their relative speeds to that frame as being different and the distance between them contracting.

 

[name123]

The Sausage crew would see the newly nearest Pastry clock as all showing 1.00s. Their own wristwatch would show 0.80s. However if the crew in the front and in the back of Sausage compared their wristwatches, they could be hours off. Obviously the Pastry clocks would be off by the same amount AND 0.20s ahead.
The Pastry's clock nearest at the time of start would now be 0.6 light seconds away and showing 0.80s.

If the Sausage crew resynchronized the clocks after the start, that needs to be said explicitly.

I had thought the crew on the sausage ship would have thought their acceleration to be pretty much instantaneous. Especially given that each segment has its own rockets. But you seem to be suggesting that the crew on the front segment and the crew on the back segment could be in disagreement about this, one of them instead of thinking that it having been an almost instantaneous acceleration and that they had traveled at the velocity of 0.6c for 1 second, would be thinking it had been going on for possibly hours.

Would you mind if I asked you the question again: At that point what roughly would the observers on the front and end of the sausage ship think the last "pastry" spaceship clock each had passed was showing on its clock?

In reply would you mind telling me roughly the actual time on those two clocks.

 

[name123]

To supply the symmetry you seem to feel is lacking, you could add two more clocks to the example above: clock F which is a pastry clock to the right of clock D and clock E which is a sausage clock to the right of clock A. Then if you consider what time reads on clock F when it meets clock E you get 1.333... yrs, (the same as clock A reads when it meets clock B), and you get 1.666... yrs for the time on clock E when it meets clock F ( the same reading as clock B reads when it meets clock A)

Yes, sorry I had misinterpreted the diagrams, thanks for clearing that up.

 

[name123]

Any connection between the segments is not relevant.
Take two ships, one behind the other. Both are accelerating such that, as measured by each ship, the distance between their ship and the other ship remains fixed, and the relative speed between them is zero. They will observe each others clocks as running at different rates, with the lead ship's clock running faster.
It is the frame that they are accelerating with respect to that would measure their relative speeds to that frame as being different and the distance between them contracting.

Which is what I was finding strange. So if we imagine the segmented "sausage" ship, and imagine that the segments are not connected, and all but the first and last segment removed, that from the pastry ship's perspective if they both accelerated (in the direction of last to first) that the first would appear, and a given point of time during the acceleration, to have a higher relative speed than the last.

The reason I find that strange is that supposing there was only one segment, it would seem to imply that where it started from would influence how fast it appeared to be going at a given point in time, from the pastry ship's perspective. Because you seem to be suggesting that if it took off from the position of the last segment, it would be measured as going slower at a given point in time from if it had taken off from the position of the first segment. I have presumably yet again misunderstood. Is it that the slower one appears to accelerate for longer? If so then it would appear to be a similarly weird situation, where where it took of from would influence how long it took to perform the acceleration.

 

[stevendaryl]

The reason I find that strange is that supposing there was only one segment, it would seem to imply that where it started from would influence how fast it appeared to be going at a given point in time, from the pastry ship's perspective. Because you seem to be suggesting that if it took off from the position of the last segment, it would be measured as going slower at a given point in time from if it had taken off from the position of the first segment. I have presumably yet again misunderstood. Is it that the slower one appears to accelerate for longer? If so then it would appear to be a similarly weird situation, where where it took of from would influence how long it took to perform the acceleration.

Think of the analogy with circular motion. Suppose you have a car that is traveling in a circle of radius 1 kilometer. A second car keeps at a constant distance of 0.25 kilometers away from the first car. Then the second car is traveling in a circle also, but a circle of a larger radius 1.25 kilometers. If the second car tried to travel in a circle of the same radius as the first car, then you would not keep the same distance between the cars.

A rocket undergoing constant acceleration is not traveling in a circle in space, instead, it's traveling in a hyperbola in spacetime. If you plot $x$ versus $t$ it traces out a hyperbola. A hyperbola is like a circle in two ways: (1) It has a "center" (but the center is a particular value of $x$ and $t$, rather than a point in space), (2) it has a "radius", which characterizes how strongly the rocket is accelerating. In the same way that two cars traveling in a circle can't maintain the same distance unless one is traveling at a greater radius, two rockets traveling along a spacetime hyperbola can't maintain the same distance unless one is traveling at a greater radius, as well.

Mathematically, the path of a circle can be parametrized by:

$x = R cos(\theta)$
$y = R sin(\theta)$

The path of an accelerating rocket can be parameterized similarly by:

$x = R cosh(\theta)$
$ct = R sinh(\theta)$

where $cosh$ and $sinh$ are the hyperbolic cosine and hyperbolic sine. If you work out what the proper acceleration for such a path is (the proper acceleration is the acceleration "felt" by those onboard the rocket), it's given by:

$g = \frac{c^2}{R}$

So a rocket that is farther ahead will have a larger value of $R$ and so a smaller value of the acceleration $g$.

That doesn't mean that the acceleration is position-dependent. A rocket at any position can travel at any acceleration. But if you want two rockets to have the same "center" ($x=0, t=0$) then the rocket with the larger radius will have the smallest acceleration. The rocket that is ahead can have a different center, but in that case, it won't maintain the same distance from the first rocket.

 

[name123]

Think of the analogy with circular motion. Suppose you have a car that is traveling in a circle of radius 1 kilometer. A second car keeps at a constant distance of 0.25 kilometers away from the first car. Then the second car is traveling in a circle also, but a circle of a larger radius 1.25 kilometers. If the second car tried to travel in a circle of the same radius as the first car, then you would not keep the same distance between the cars.

I do not understand why not. If two cars each traveled at the same speed in a circle of the same radius with the same centre, then the distance between them would remain constant I would have thought. I am imagining the chord length, and angle between them would remain the same.

That doesn't mean that the acceleration is position-dependent. A rocket at any position can travel at any acceleration. But if you want two rockets to have the same "center" ($x=0, t=0$) then the rocket with the larger radius will have the smallest acceleration. The rocket that is ahead can have a different center, but in that case, it won't maintain the same distance from the first rocket.

I do not know why the centre is important, I would have thought all observers, regardless of x position in the rest frame will agree on the speeds of the rockets.

 

[stevendaryl]

I do not understand why not. If two cars each traveled at the same speed in a circle of the same radius with the same centre, then the distance between them would remain constant I would have thought.

I meant that they are traveling in concentric circles of different radii.

I do not know why the centre is important, I would have thought all observers, regardless of x position in the rest frame will agree on the speeds of the rockets.

It's not an x-position, it's a center in spaceTIME. So the center is defined by a value of $x$ and a value of $t$.

If you have a rocket moving at constant acceleration (as felt by those on board the rocket), then its path will be described by the pair of equations:

$x = x_0 + R cosh(\theta)$
$t = t_0 + R/c sinh(\theta)$

So there are two different choices to be made (for motion along the x-axis):

1. The "center" of the motion, the point $(x_0, t_0)$.
2. The "radius" of the motion, $R$

If the centers of two different rockets are different, then the distance between the rockets, as measured by those aboard the rocket, will not be constant. So for the rockets to stay the same distance apart, as measured by those on board, you have to have the centers the same, and the only difference is different values of $R$. The acceleration felt by those on board the rocket is $\frac{c^2}{R}$, so the rocket with the greater value of $R$ will feel a smaller acceleration.

You can certainly have two rockets with the same value of $R$ (which means the same acceleration), but with different "centers". But then rockets would not stay the same distance apart, as viewed by those aboard the rocket.

 

[name123]

I meant that they are traveling in concentric circles of different radii.

Oh ok, I was confused when you wrote

If the second car tried to travel in a circle of the same radius as the first car, then you would not keep the same distance between the cars.

But you are actually saying that if the second car tried to travel in a circle of the same radius as the first car, then they would keep the same distance between the cars if they were traveling at the same speed?

It's not an x-position, it's a center in spaceTIME. So the center is defined by a value of $x$ and a value of $t$.

I realize the centre is not an x-position as it has a time coordinate. What I was assuming was that all observers, regardless of x position in the rest frame will agree on the speeds of the rockets, for a given t in that rest frame. So that the "centre in spacetime" would be irrelevant. As the $x$ value in that rest frame did not matter. Only the $t$ value.

 

[stevendaryl]

I realize the centre is not an x-position as it has a time coordinate. What I was assuming was that all observers, regardless of x position in the rest frame will agree on the speeds of the rockets, for a given t in that rest frame. So that the "centre in spacetime" would be irrelevant. As the $x$ value in that rest frame did not matter. Only the $t$ value.

The x-value of the center doesn't matter for the speed as computed by someone at rest, but it does matter for the distance as measured by someone on board the rocket. For the distance between the rockets to be constant, as measured by those on the rockets, then the rockets have to have the same "center".

 

[jartsa]

Is it that the slower one appears to accelerate for longer? If so then it would appear to be a similarly weird situation, where where it took of from would influence how long it took to perform the acceleration.

So now there is even an end to the accelerations of the two ships?

Well, if the reason that the acceleration ends is that all fuel has been burned, then the ship that burns fuel at faster rate, in order to accelerate at faster rate, will stop accelerating first. This is according to the "pastry ship".

The above is a quite good way to have an end of acceleration, as the two ships end up with the same kinetic energy, after burning the same amount of fuel.

 

[name123]

The x-value of the center doesn't matter for the speed as computed by someone at rest, but it does matter for the distance as measured by someone on board the rocket. For the distance between the rockets to be constant, as measured by those on the rockets, then the rockets have to have the same "center".

In post #61 when I was replying to Janus, I was discussing the perspective of the person at rest (on the pastry spaceship). I think Janus was too, and as I understood it was suggesting that the front segment would appear to be going faster to someone on the pastry spaceship. At least that it what I understood him to be stating when he wrote

If you arranged things so that in the sausage frame, the spacing between segments remained constant and all the segments started and stopped accelerating at the same moment, then according to the pastry ship, the segments and thus the distance between them was shrinking due to length contraction during this whole acceleration. But this also means that, at any given moment the Leading segment was traveling at a lower speed relative to the rear segment and thus its clock was exhibiting a greater time dilation rate. In other words, according to the pastry ship, the clocks in the segments wouldn't be ticking at the same rate.

 

[stevendaryl]

In post #61 when I was replying to Janus, I was discussing the perspective of the person at rest (on the pastry spaceship). I think Janus was too, and as I understood it was suggesting that the front segment would appear to be going faster to someone on the pastry spaceship. At least that it what I understood him to be stating when he wrote

I'm a little confused about the sausage versus pastry thing, but in terms of two accelerating rockets, there are two different frames to consider: (1) the frame of someone on board the rocket (the rocket frame), (2) the frame of someone who is not accelerating (the inertial frame)

If the distance between rockets is constant as measured in the rocket frame, then

1. The acceleration felt by the rear rocket will be greater than that of the front rocket
2. The distance between rockets is shrinking as measured in the inertial frame

If the distance between rockets is constant as measured in the inertial frame, then

1. The acceleration felt by the two rockets is the same
2. The distance between rockets is growing as measured in the rocket frame.

 

[SlowThinker]

I had thought the crew on the sausage ship would have thought their acceleration to be pretty much instantaneous. Especially given that each segment has its own rockets.

Yes.

But you seem to be suggesting that the crew on the front segment and the crew on the back segment could be in disagreement about this, one of them instead of thinking that it having been an almost instantaneous acceleration and that they had traveled at the velocity of 0.6c for 1 second, would be thinking it had been going on for possibly hours.

You are assuming a step, resynchronization of Pastry's clocks, that doesn't happen.

Each Pastry crewman would see, using his wristwatch, that the acceleration started at 0.00s, and ended at say 0.001s. Then they started to decelerate at 0.800s and finished at 0.801s. Again, each crewman would see the same.
But if, during the way (the 0.8s they are moving), they looked around, they would "see" (rather "compute" or "estimate") the wristwatches toward the front showing some time in the past, and the wristwatches behind as some time in the future.
(If you factor in the light delay, everyone should see that the trip occurs from 0.000 to 0.801s Pastry wristwatch time, for everyone. It's better not to think of light delay yet and certainly it's a bad idea to think of it only sometimes).

If everyone resynchronized their wristwatches when they started to move, they would need to agree on a master clock, say the central one. So the crewman in the middle would keep the wristwatch at 0.001s, but those in front would move it from 0.001s to say -750 and those in the back to say +750.
(If the trip never stopped, they could now walk around, comparing wristwatches, and they would agree that indeed all their clocks show the same time.)
Then the trip would stop at 0.8s central clock, -749.2 front clock, 750.8 rear clock. Again, after stopping, they would realize that the clocks are not synchronized any more, and would need to adjust them again.

Would you mind if I asked you the question again: At that point what roughly would the observers on the front and end of the sausage ship think the last "pastry" spaceship clock each had passed was showing on its clock?

In reply would you mind telling me roughly the actual time on those two clocks.

With the resynchronization, it's needlessly confusing. Just add or subtract 750s to Pastry clock as above.
Without the resynchronization,
Front Pastry clock: 0.800s
Sausage clock nearest to Pastry's front: 1.000s
Back Pastry clock: 0.800s
Sausage clock nearest to Pastry's end: 1.000s
Note: Pastry is the accelerating/decelerating one.