hogrampage
- 107
- 1
Homework Statement
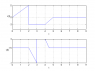
Express y(t) as a function of x(t).
https://www.physicsforums.com/attachment.php?attachmentid=61309&d=1378005939
Homework Equations
The Attempt at a Solution
Transformations:
-x(t)
0.5x(t)
x(2t)
x(t-2)
x(t)+1.5
∴y(t) = -0.5x(2t-4)+1.5
Here is the plot:
As seen in the plot above, it is different from the figure in the book (P2.4(b)) on the time interval 4 < t < 5. Where am I going wrong?
Thanks!
Attachments
Last edited: