I Fınding the position of a point on the line

AI Thread Summary
To find the coordinates of point Q on line l_1 that is closest to point P, the perpendicular distance from P to l_1 must be calculated. The equation of the line l_1 is given as ax + by + c = 0, and the coordinates of P are (x_p, y_p). A common method involves using the formula for the projection of point P onto line l_1, resulting in an expression for Q in terms of P and the coefficients a, b, and c. This approach yields a single equation that defines point Q's coordinates. The discussion emphasizes the need for a concise mathematical representation of Q based on the given parameters.
Arman777
Insights Author
Gold Member
Messages
2,163
Reaction score
191
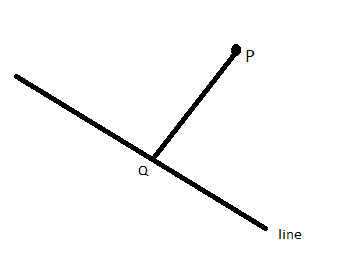
Let us suppose we have a line ##l_1 = ax + by + c = 0## and we have a point P, ##P(x_p, y_p)## that is outside of this line. If we draw a perpendicular line from point ##P## to a point on the ##l_1##. What would be the coordinates of this point ? I know there are many ways to do it. But I am looking for a single equation that can describe this point (##Q##) ?

1565105884095.png
 
Mathematics news on Phys.org
Have you considered using one of those methods to solve the problem, which should give you an expression for Q in terms of P and l_1?
 
  • Like
Likes Vanadium 50 and Mark44

Thread 'Trigonometry problem of interest'

Seemingly by some mathematical coincidence, a hexagon of sides 2,2,7,7, 11, and 11 can be inscribed in a circle of radius 7. The other day I saw a math problem on line, which they said came from a Polish Olympiad, where you compute the length x of the 3rd side which is the same as the radius, so that the sides of length 2,x, and 11 are inscribed on the arc of a semi-circle. The law of cosines applied twice gives the answer for x of exactly 7, but the arithmetic is so complex that the...
View full post »

Similar threads

I Prove that the geometric mean is always the same
Replies
2
Views
2K
I On a proof of the converse of the supporting hyperplane theorem
Replies
9
Views
2K
B Existence of parallels in axiomatic plane geometries
Replies
36
Views
5K
I How can you represent a point by "z = x + iy" as shown here?
Replies
10
Views
2K
A check: shortest distance from point to line
Replies
2
Views
2K
MHB Parametric Eqs: Find Line & Plane, Find Triangle Area
Replies
4
Views
1K
B Invariant under rotation: Banal, obvious, or noteworthy?
Replies
2
Views
2K
I Expressing any given point on plane with one unique number
Replies
4
Views
2K
I Two vectors and two perpendicular lines
Replies
20
Views
2K
MHB Determining c in Quadratic Function Turning Point
Replies
6
Views
2K

Hot Threads

Recent Insights

Back
Top